范圍最近鄰查詢方法研究
劉 彬,王建國
(1.泰山學院信息科學技術學院;2.泰山學院教務處,山東泰安 271021)
1 引言
最近鄰(Nearest Neighbor,簡稱NN)查詢是空間數據庫中一種重要的查詢類型,傳統的NN查詢是指查詢離給定點最近的對象,稱為點的最近鄰(Point NN,簡稱PNN)查詢[1].Tao等人提出的連續最近鄰(Continuous NN,簡稱CNN)查詢[2],可以有效地檢索一條線段上所有點的最近鄰,此查詢的輸入限定在一維線段上.
本文提出了二維情形下的最近鄰查詢問題——“范圍最近鄰”(Range NN,簡稱RNN)查詢.在二維情形下,給定一個數據集,RNN查詢檢索矩形里每一個點的最近鄰.RNN查詢的應用比較廣泛,比如在移動環境中,用戶在確定查詢點時,由于定位方法的原因,他們沒有辦法找到自己的準確位置.即使能準確定位,他們也可能由于個人原因沒有辦法將準確位置提供給服務商.RNN查詢解決了這個問題,因為它查詢的是范圍的最近鄰而不是點的最近鄰.大量的2G/3G移動用戶更適合使用這種查詢,因為這些設備不支持連續最近鄰,他們可以將RNN查詢闡述成“尋找離城市公園最近的旅社”這樣的問題.再如,一個用戶當在附近走動的時候可能會持續地尋找最近鄰,向服務器分別提交這些PNN查詢是低效的.一個更好的方法是進行RNN查詢來獲得這個范圍所有可能的最近鄰.在這個范圍內的任何PNN查詢都可以在這個預先取出的集合中獲得,這將節省計算和通信的代價.這說明RNN查詢適用于小范圍內的不同用戶進行PNN查詢的情形.由于空間鄰近的PNN查詢范圍相同的R樹結點.如果對這些點進行分組處理,將他們歸屬于不同的范圍,然后進行RNN查詢,在RNN的基礎上找到PNN,將會提高效率.本文主要研究范圍最近鄰查詢的性質和基本處理思想.
文章第2部分回顧CNN查詢的一些相關知識;第3部分給出RNN查詢的正式定義,分析查詢性質,并通過一個例子描述了LNN(Line NN)算法的基本處理過程;第4部分分析LNN算法的時間復雜度;最后,提出了一些未來研究的方向.
2 相關工作
Song等人在文獻[3]中第一次提出了“連續最近鄰”查詢的概念,一個CNN查詢查找一個移動對象的最近鄰,更具體地說,它查找一條線段上所有點的最近鄰.為了處理CNN查詢,Song提出了在線段上反復對一些取樣點進行NN查詢,在[2]中,Tao等人詳細說明了CNN處理算法.他們證明了這條線段包含一個“分割點”的集合,其中每一個分割點有兩個相同距離的最近鄰對象,并且這些最近鄰對象組成了CNN集合.因此,CNN問題等價于遍歷R-樹時找到和儲存那些分割點,為了刪除不必要的結點存取,他們提出了三個規則:
1)對于一中間結點E和查詢線段q,刪除mindist(E,q)>SLMAXD的結點,SLMAXD是所有分割點和它的NN之間距離的最大值.
2)刪除到每一個分割點s的最小距離比s和s的NN之間距離大的結點.
3)按它們的MINDIST值遞增訪問結點.
Tao等人將這些規則分別通過廣度和深度優先搜索來實現,并更進一步推廣這些算法來解決kCNN查詢,kCNN查詢找到的是一條線段上所有點的k個最近鄰.
3 范圍最近鄰查詢(RNN查詢)
3.1 RNN查詢的定義
定義1 給定一個二維空間的數據集R2,一個矩形A(邊界在內)的范圍最近鄰(RNN)的集合可以表示為RNN(A),即為A中每一個點的最近鄰(NN)的集合.有:

NN(p)表示點p的最近鄰,A稱為查詢范圍在二維情形下為矩形,當它在零-維和1-維空間中,RNN分別變為PNN和CNN.
本文采用歐氏距離,這意味著每一個對象是一個點或者可以被一個點來代表,因此本文限定數據集合于為點數據集.
3.2 RNN查詢的性質
根據定義1可知任何一個A中的對象是A的一個RNN,我們稱它為內部RNN,因此我們主要是尋找外部RNN,也就是A外的RNN.
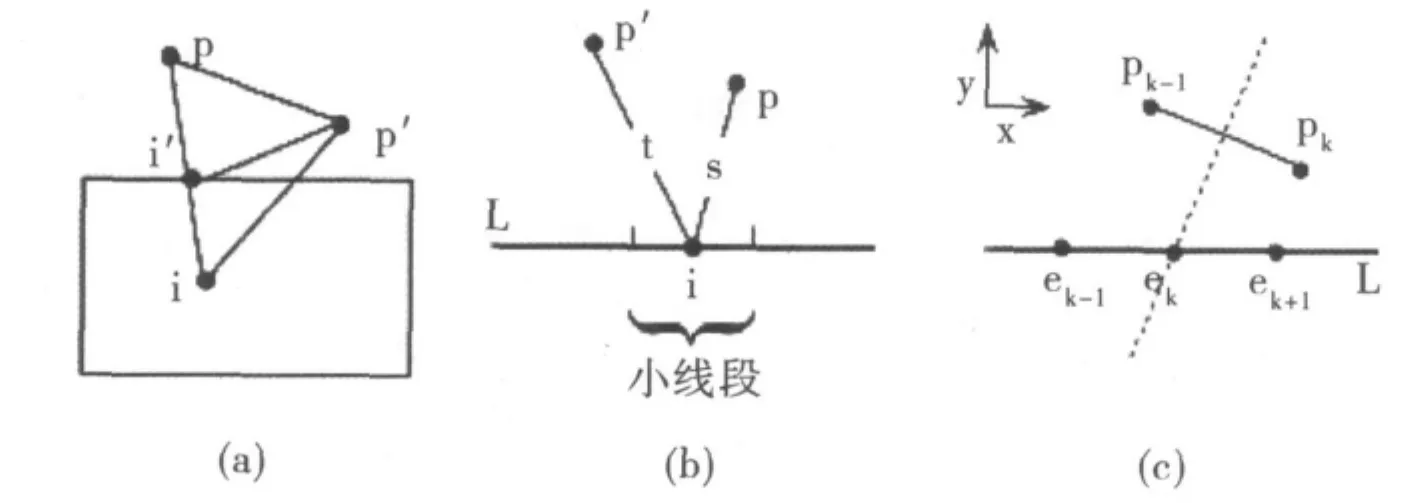
圖1 引理1、2、4的證明輔助圖
引理1 一個對象p成為A的一個外部RNN的充要條件是p不在A內而是A邊界上的至少一個點的NN.
證明:必要條件從定義中可以看出是顯然的.充分條件可以通過反證法來證明:假定p不是A邊界上的任何一個點的NN,但p是一個RNN2,則p至少是A內一個點i的NN,如圖1(a),i'表示線段和 A邊界的相交點.由于p不是i'的NN,則必有另一個對象p'使得比短,也就是說,,在不等式的兩邊加上,我們得到,這和我們的假設p是i的NN相矛盾.因此假設錯誤,充分條件得證.
引理1告訴我們查詢A的外部RNN和查詢A邊界上每個點的NN是等價的,A的邊界包含四條線段,因此,這個問題就可以轉化為查找一條線段L上所有點的NN,這些NN稱為L的線段最近鄰(LNN).
證明:假定L上有一個點i,L的NN是p且p'是i的第二最近鄰(如圖1(b)),設s表示,t表示,取L上一個小線段
引理2 線段L可以被劃分為有限數量的小線段,小線段上的每一個點有相同的NN.,則它上面的所有點的NN為p,因為它們到p的距離總是比s+小,并且它們到p'后其他對象的距離總是比大.由于L的長度是有限的且這個小線段有固定的長度t-s,因此這些小線段的數量是有限的.
引理3 如果任何兩個鄰近的小線段有不同的NN,那么,所有的小線段都有不同的NN.
通過對前面引理的證明,引理3是比較明顯的,它說明了一個對象最多可以成為一條小線段的NN.
引理4 設e1,e2,…表示從左到右所有小線段的末端點,p1,p2,…表示每條小線段的NN.那么,對任意i<j,有pi·x<pj·x,其中p·x表示對象p在L上的投影值.
證明:通過反證法來證明這個引理.如果引理不成立,則至少兩個相鄰的小線段違背這個規則,假設是和,存在·x(見圖2c).因此,pk在的垂直平分線的左邊,而在右邊,那么L上ek左邊的點離比離pk近,反之亦然.這就與是的NN且pk是的NN相矛盾,引理成立.
3.3 算法處理過程
在這些引理的基礎上,下面通過一個例子來說明LNN算法的基本思想.首先通過對象p在L上的投影值來決定要處理的對象的順序,如圖1所示,處理順序為p1,p2,p3,p4,p5(在兩個或更多個對象有相同投影值的情況下,只保留離L最近的對象).然后,計算每個對象所對應的小線段,如果一個對象沒有相應的小線段,這意味著這個對象不是一個LNN.這些小線段的端點可以通過L和每一對連續對象的垂直平分線的交點來計算獲得.在圖1中,最初e1=L.min是p1對應小線段的左端點,當處理p2時,e2作為p2的左端點(也是p1的右端點);然而,當p3被處理時的垂直平分線與L相交在e2左邊某個地方的一個點,這意味著p2沒有對應的小線段,因為p1或 p3比p2到L上的任何一點要近.因此p2不是一個LNN,故被移除.這樣p1和p3成為連續的對象,p3對應小線段的左端點即被重新計算,由于位于e2的左端,說明上的點距p3比距p1更近,因此e2被移除.接著處理p4,并得到e3作為p4相應小線段左端點.最后處理p5,但的垂直平分線沒有與L相交,這意味著p5沒有小線段,不是一個LNN.由于p4是保留的最右邊對象,它的小線段的右端點為e4=L.max,這樣所有點被處理完.得到結果:p1,p3和p4是LNN,相應的小線段是和.
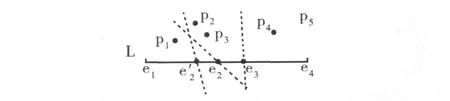
圖2 LNN查詢示例
4 算法性能分析
LNN算法處理過程分為兩個階段,第一階段是通過對查詢對象的排序來決定對象的處理順序,第二階段是掃描對象并計算對應小線段的端點.
排序可以使用快速排序方法[4],在最好情況下花費O(nlogn)的時間代價,在最壞情況下花費O(n2)的時間代價,平均時間代價通過推算可以得知為O(nlogn);在掃描過程中需要計算小線段的端點,假設每次計算的時間為c(c為任意常數),則整個掃描時間為cn,因此掃描過程的時間代價為O (n).如果程序由兩部分(兩組語句或者兩段代碼)順序組成,我們只需要考慮其中開銷較大的部分,因此LNN算法的時間復雜度是O(nlogn).
5 結束語
文章提出范圍最近鄰(RNN)查詢作為點最近鄰(PNN)和連續最近鄰(CNN)查詢的擴展,并在2D空間中分析了查詢的性質,提出了算法基本思想并作了性能分析.未來的工作將致力于動態數據集中范圍最近鄰查詢的研究.
[1]N.Roussopoulos,S.Kelley,F.Vincent.Nearest neighbor queries[A].Proc.of the ACM SIGMOD Intl.Conf.on Management of Data[C].New York:ACM,1995.
[2]Y.Tao,D.Papadias,Q.Shen.Continuous nearest neighbor search[A].In Proc.of 28th Intl.Conf.on Very Large Data Bases (VLDB)[C].Hong Kong:VLDB Endowment,2002.
[3]Z.Song,N.Roussopoulos.K-Nearest Neighbor Search for Moving Query Point[A].Proc.Symp.Spatial and Temporal Databases[C].Berlin:Springer,2001.
[4](美)Clifford A.Shaffer.數據結構與算法分析(Java版)[M].北京:電子工業出版社,2001.

