橢圓環形剛體轉動慣量的數值計算
于志明
(連云港師范高等專科學校物理系 江蘇 連云港 222006)
文獻[1]討論了橢圓環形剛體的轉動慣量,結果用橢圓積分給出,使用時要查《橢圓積分表》,很不方便.我們用Matlab編程對橢圓環形剛體的轉動慣量進行了數值計算和多項式擬合,可以快速計算出橢圓環形剛體的轉動慣量.
1 橢圓環形剛體的轉動慣量

圖1
如圖1所示,一質量為m,半長軸為a,半短軸為b的均質橢圓環形剛體,其解析方程可表示為

(1)
其周長為
(2)
該橢圓環形剛體對過環中心且與環面垂直的軸線的轉動慣量可表示為
I=
(3)

(4)
則式(3)變為
I=
(5)
令I(n)=
(6)
則式(5)變為
I=ma2I(n)
(7)
由式(6)定義的I(n)只與n有關,也即只與橢圓的具體形狀有關.由式(7)可知,只要計算出I(n),就計算出了橢圓環形剛體的轉動慣量.但I(n)的分子、分母是兩個比較難的積分.根據文獻[1],可以將I(n)用橢圓積分來表示,結果為
(8)
式(8)中的F(k)為
(9)
為第一類全橢圓積分.式(8)中的E(k)為
(10)
為第二類全橢圓積分.式(8)、(9)、(10)中的k為橢圓的偏心率,k與n的關系為
(11)
式(8)具體的積分結果要根據k值查橢圓積分表,這顯然很不方便.因而,我們設法對I(n)作數值計算,進而實現對橢圓環形剛體轉動慣量的數值計算.
2 橢圓環形剛體轉動慣量的數值計算
根據文獻[2],利用Matlab的數值積分指令編程,先對I(n)的分子、分母中的兩個積分進行數值計算,進而算得I(n).具體程序為


'x','n');
s1=quad(y1,0,pi/2,[],[],n);
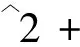
s2=quad(y2,0,pi/2,[],[],n);
I=s1/s2
取定n,將其填入第2,4句中,就可以得到相應的I(n).
如當n=0時,I(n)=0.333 3;
當n=0.215時,I(n)=0.391 7;
當n=1時,I(n)=1;
當n=5.1時,I(n)=9.967 9;
當n=11.5時,I(n)=45.6787;
……
這比通過查橢圓積分表求I(n)方便多了.
如在上邊的程序中加上循環語句,就可以一次連續計算出很多與n相應的I(n),進而可以畫出I(n)與n的關系曲線,從中可以看出I(n)隨n的變化規律.圖2給出了n在0~20之間取值時I(n)隨n變化的情況.

圖2
由對I(n)數值計算的結果,利用Matlab中的多項式擬合指令,還得到了I(n)的多項式表達式,結果為
I(n)=0.000 4n3+0.315 9n2+0.246 1n+0.333 3
(12)
因此,橢圓環形剛體的轉動慣量可表示為
(13)
將橢圓環形剛體的質量m,半長軸a,半短軸b的值代入式(13),可以計算出該橢圓環形剛體的轉動慣量.
參考文獻
1 趙新聞,周欣然,楊兵初.橢圓環形剛體的轉動慣量.大學物理,2008,27(6):13~14
2 彭芳麟,管靖,胡靜,盧圣治.理論力學計算機模擬.北京:清華大學出版社,2002.66~69

