巧用運動合成分解法解決復雜問題
張錦科
(張家川縣第二中學 甘肅 天水 741506)
在中學物理教學中,不僅要注重物理基礎知識的教學,注重對學生進行基本的解題原理、解題方法和思路的訓練,而且有必要使學生理解和掌握一些典型的科學思維方法和解題技巧.對于同一個物理問題,往往能從不同的角度去思考和分析,采用不同的方法來解決,但繁簡程度卻可能有很大的區別.如果遵循一定的科學思維方法,掌握一定的解題技巧,則往往會事半功倍,得心應手.
運動的合成與分解是研究運動的基本方法,是將復雜的、生疏的運動分解成簡單的、熟悉的運動進行研究的方法,這是一種技能.這種處理問題的方法可以變曲線運動為直線運動,變復雜運動為簡單運動,從而使問題的解決得到明顯的簡化.
【例1】 一質點從高處自由下落距離h后,落到傾角為45°很長的光滑斜面上,并與斜面發生多次彈性碰撞(圖1).選取直角坐標,重力加速度為g.求:
(1)經過n次(n=1,2,3,…)碰撞后剛彈起時速度的x分量和y分量;
(2)任意兩次碰撞之間的時間間隔.
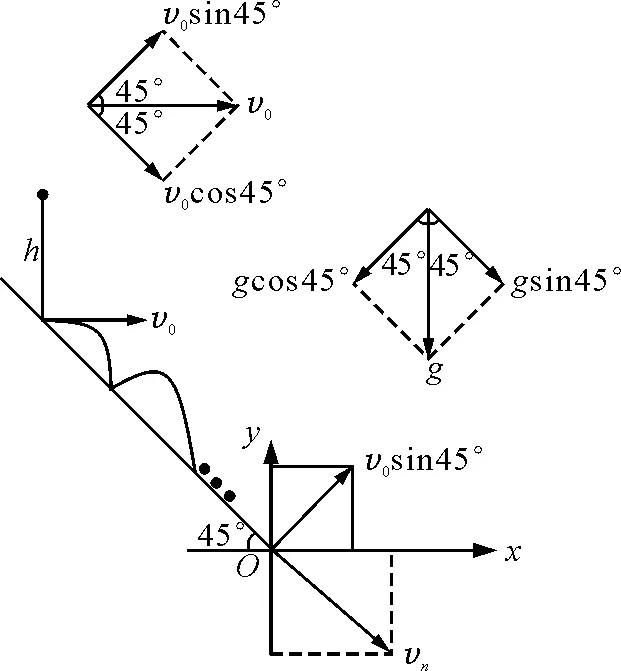
圖1
解析:小球的運動可分解為沿斜面向下加速度為a∥=gsin45°的勻加速運動和垂直斜面加速度為a⊥=gcos45°的來回反彈運動,如圖1所示(類似相對于斜面的豎直上拋運動).
小球與斜面每連續碰撞兩次之間的時間間隔就等于小球在垂直斜面方向上來回運動一次的時間.由于在垂直斜面的方向上,任一來回小球的位移為零,沿這個方向的分力不做功,因此每次與斜面碰前或碰后瞬間,在垂直斜面方向上的分速度的大小始終不變,即相鄰碰撞兩次之間的時間間隔是相等的.
設小球第一次與斜面碰前瞬間速度為v0,則
(1)
(2)
根據“反射定律”,第一次碰后的速度v0是水平的.把v0分別沿斜面和垂直斜面分解作為兩個分運動的初始速度.即沿斜面為v1∥=v0cos45°,垂直于斜面為v1⊥=v0sin45° .
設每兩次碰撞之間的時間間隔為Δt,根據前面分析有
(3)
第n次與斜面碰撞,小球所經歷的時間為
tn=(n-1)Δt
(4)
設此時沿斜面的分速度為vn,則
vn=v0cos45°+a∥tn=
v0cos45°+gsin45°(n-1)Δt
(5)
建立直角坐標系,第n次碰后瞬間垂直斜面方向的分速度和沿斜面的分速度分別如圖1所示.因此水平速度為
vx=vncos45°+v0sin45°sin45°
(6)
聯立(2)、(3)、(5)、(6)式,得
豎直速度為
vy=vnsin45°-v0sin45°cos45°
(7)
聯立(2)、(3)、(5)、(7)式,得
點評:在教學中要利用不同類型的典型題進行一題多解的訓練活動,這樣不僅可以破除學生的定勢思維,也可以拓寬學生的視野和思路,達到舉一反三、觸類旁通的目的;還可以激發學生學習的濃厚興趣,有利于培養學生思維的敏捷性和變通性.在解題訓練過程中,要有意指明解題的思想方法和各方法的特點,以及在解決不同問題時的優勢和不足.學習物理就要學習物理思想和研究問題的方法,這樣才能在學習物理知識的過程中培養能力,才能適應時代,不斷創新.
【例2】如圖2所示,傾角為α的光滑斜面固定在地面上不動,一個小鋼球以角β飛向斜面,試問β為何值時,球可以返回到它第一次與斜面相碰的點?(所有碰撞都可認為是彈性的)
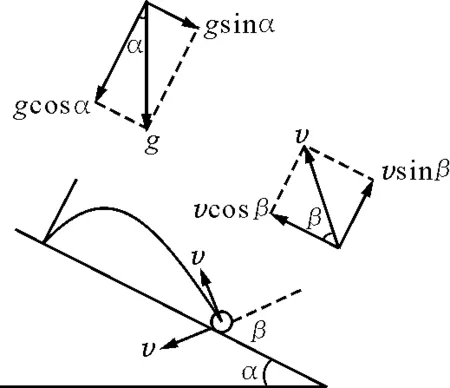
圖2
解析:小球的運動可分解為沿斜面向上的勻減速運動(往返)和垂直斜面的來回反彈運動,如圖2所示.小球如能回到入射點,則由機械能守恒定律知,小球回到該點時的速度大小與入射時的速度大小相等.設小球第一次碰撞的速度為v,小球回到入射點時與斜面碰撞了n次,經歷時間為t,由平行斜面方向的運動
由垂直斜面方向的運動
聯立兩式可得
解得
β=arccot(ntanα) (n=1,2,3,…)
點評:本題分別將速度和加速度沿斜面和垂直斜面分解,直接導致了解題的便捷.因此在實際中,要培養學生打破“平拋”分解模式,靈活地分解,從而達到巧妙、簡潔地解題目的.對比例1和例2,說明題目雖千變萬化,但萬變不離其宗,這“宗”即解題的思想方法.
【例3】 制備納米薄膜裝置的工作電極可簡化為真空中間距為d的兩平行極板,如圖3(a)所示.加在極板A,B間的電壓UAB做周期性變化,其正向電壓為U0,反向電壓為-kU0(k>1),電壓變化的周期為2τ,如圖3(b)所示.在t=0時,極板B附近的一個電子,質量為m,電荷量為e,受電場作用由靜止開始運動.若整個運動過程中,電子未碰到極板A,且不考慮重力作用.
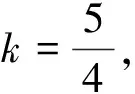
(2)若電子在0~200τ時間未碰到極板B,求此運動過程中電子速度v隨時間t變化的關系;
(3)若電子在第N個周期內的位移為零,求k的值.

圖3
解析:(1)電子在0~τ時間內做勻加速運動,加速度的大小為
(8)
位移
(9)
在τ~2τ時間內先做勻減速運動,后反向做勻加速運動,加速度的大小
(10)
初速度的大小
v1=a1τ
(11)
勻減速運動階段的位移
(12)
依據題意d>x1+x2,解得
(13)
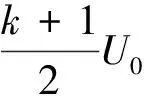
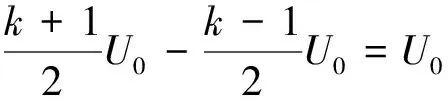
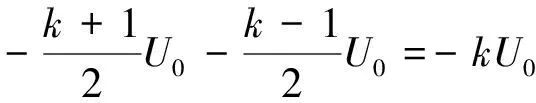
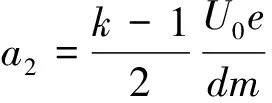
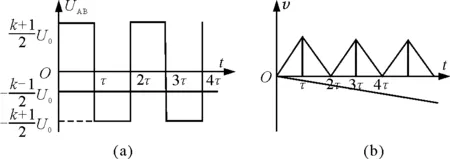
圖4
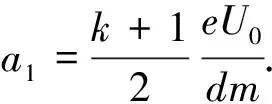
t-2nτ(0≤t-2nτ<τ) (n=0,1,2, …,99)
因此
v2n+1=a1(t-2nτ)
(14)
v2n+1'=a2t
(15)
故合速度為
u2n+1=v2n+1-v2n+1'=a1(t-2nτ)-a2t=
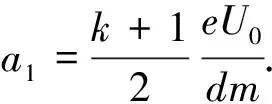
t-(2n+1)τ
[0≤t-(2n+1)τ<τ] (n=0,1,2, …,99)
因此v2n+2=a1τ-a1[t-(2n+1)τ]
(16)
v2n+2'=a2t
(17)
故合速度為
u2n+2=v2n+2-v2n+2'=
a1τ-a1[t-(2n+1)τ]-a2t=
(3)矩形電壓場中電子在第N個周期內的位移為v-t圖像[圖4(b)]中一個周期三角形的面積即
(18)
穩恒電壓場中電子反向運動的位移為前N個周期的位移減去前(N-1)個周期的位移即
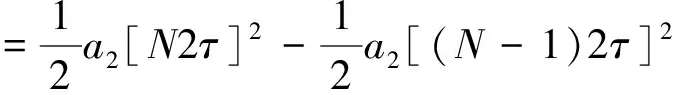
(19)
依題意xN-xN'=0
(20)
聯立解得
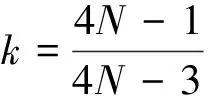
點評:2010年江蘇高考壓卷題偏難,頗有競賽題風格.參考答案數學味太濃,很多學生看完答案后不知所云.利用分解與合成的方法,使對試題的理解變得容易,有效減小了思維量.對稱矩形場中電子的運動我們比較熟悉,即先向上勻加速再向上勻減速運動,而且兩段對稱,做題時要充分利用這一結論.

