簡諧波傳播時介質質點的運動性質解析
邵武兵
(浙江省普陀中學 浙江 舟山 316100)
在機械波的教學中,學生往往會提出疑問:簡諧波在介質中傳播時,介質的質點究竟做什么運動?
學生之所以會提出這個問題,是因為在文獻[1]第25頁,對機械波是這樣闡述的:組成介質的質點之間有相互作用,一個質點的振動會引起相鄰質點的振動.機械振動在介質中傳播,形成了機械波.
結合文獻[1]對繩波產生過程的分析,我們知道,振動之所以能夠在介質中傳播是因為介質中各質點之間存在相互作用力,一旦介質中的某一質點產生振動,首先振動起來的質點就會“帶動”周圍的質點一起振動,被帶動的質點又會帶動它后面的質點振動,這樣依次帶動,振動就會由近及遠地傳播,從而形成機械波.
從上述分析可知,這種“帶動”從本質上講就是每前一個質點給后一個質點一個周期性的外力(驅動力),所以介質的質點應該是做受迫振動.
然而,文獻[1]第27頁在闡述正弦波,也叫簡諧波時,有這樣一句話“介質中有正弦波傳播時,介質的質點在做簡諧運動.”
由此學生就產生疑問:在簡諧波傳播時,介質的質點到底是做受迫振動呢?還是做簡諧運動?
實際上對介質質點所做的運動,確切說法應該是質點做與簡諧運動有相同運動學性質的穩定的受迫振動.
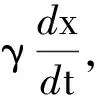
根據牛頓第二定律,得受迫振動的動力學方程式為
解此方程,根據微分方程的理論可得穩定解為
x=A0cos(ωt+φ)
這表明,上述的受迫振動是一個和簡諧運動形式相同的等幅振動,振動的頻率和驅動力的頻率相同,并與驅動力f=f0cosωt之間有恒定的相位差φ.這種穩定的受迫振動的運動學方程與簡諧運動的運動學方程形式相同,所以就運動學性質而言,當驅動力為f=f0cosωt的受迫振動的運動學性質(指位移x,速度v,加速度a與時間t的關系)與簡諧運動是相同的.
這里要指出的是如果驅動力不滿足f=f0cosωt,而是t的復雜周期函數時,所得的結果就要復雜的多,振幅一般也不再是恒定不變的,其運動學性質與簡諧運動不相同.
還要指出的是盡管驅動力為f=f0cosωt的受迫振動的表達式與簡諧運動的形式相同,但由于受力情況不同,因而運動情況也還是有區別的.前者以驅動力的頻率振動,阻力所消耗的機械能由驅動力做功補償,其振幅由振動系統的性質及驅動力的性質共同決定,與初始條件無關;后者則以系統的固有頻率振動,阻力被忽略,機械能守恒,是一種理想的振動,其振幅由初始條件決定.
所以簡諧波的形成嚴格的說法應該是:運動學性質與簡諧運動相同的受迫振動在介質中的傳播所形成的波.
參考文獻
1 人民教育出版社物理室.普通高中課程標準實驗教科書物理·選修3-4.北京:人民教育出版社出版,2009

