平行光斜入射光柵（矩孔）的衍射光場

李爭路，岑 剡

（復旦大學 物理學系，上海200433）

1 引 言

衍射光柵光柵常量的測定實驗要求在測量過程中，平行光垂直光柵入射．如果平行光斜入射光柵會發生怎樣的現象？對于這個疑問，本文試圖通過理論分析和實驗驗證來回答，以幫助學生更好地理解實驗調節過程中遇到的實驗現象．

以光柵建立坐標系，如圖1所示（灰色代表不透光部分，白色代表透光部分），垂直入射時，入射光平行于ζ軸．

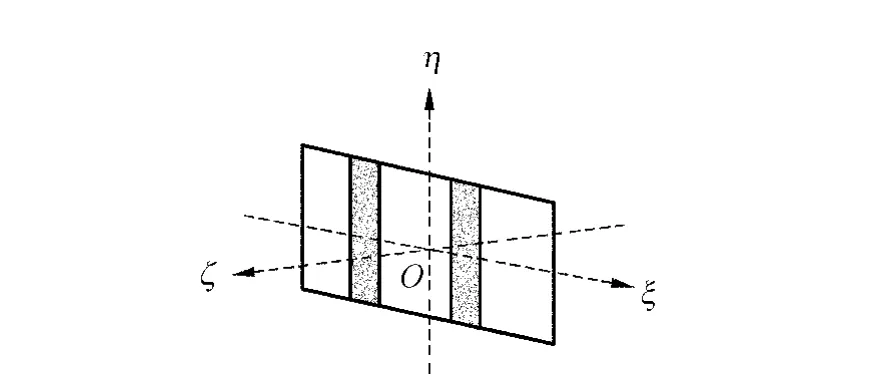
圖1 坐標系的建立

當平行光的入射方向在ζOξ平面內且與ξ軸有一定夾角時，有光柵方程［1－2］

其中，Δr為光程差，d為光柵常量，i為入射角，θ為出射角，k為出射的級次，λ為入射光波長．式中，當兩角偏向法線同側時，為加號；當兩角偏向法線異側時，為減號．

當入射平行光入射方向在ζOη平面內并且與η軸有一定夾角時，則可以看到如圖2所示的衍射光斑呈曲線形分布（后文將證明當光柵與接收屏平行時，該曲線為雙曲線）．逐漸減小入射平行光與η軸的夾角，曲線的曲率半徑將逐漸增大．

圖2 斜入射光斑分布情況（單縫衍射）

2 理論分析

采用如下的菲涅爾 －基爾霍夫積分公式［2－5］進行計算

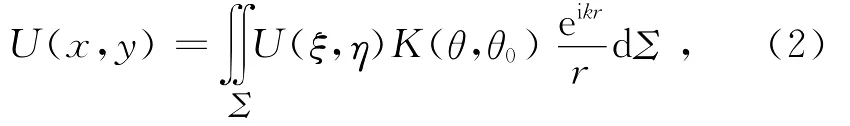
2．1 衍射后光場的計算

在傍軸條件下，且衍射場接收于薄透鏡的后焦面時，可對（2）式作近似［2］1，r＝r0＋Δr≈f，其中r0為矩孔原點O出射的光到接收屏的光程，Δr為由其他點出射光與原點出射光的光程差．于是，在接收屏x O′y 上，光程差可表示為［2］：Δr＝－（ξsinθ1＋ηsinθ2），其中θ1和θ2是二維的衍射角（衍射方向的2個方向角的余角）［2］，將上式代入（3）式，有

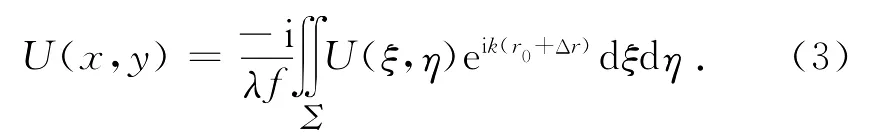
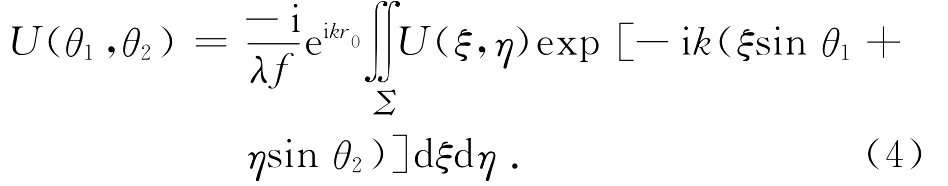
2．2 衍射前光場的計算

定義入射光方向與ξ軸及η軸夾角分別為γ和δ，利用同樣的方法［2］，可得入射前光程差為Δr＝－（ξcosγ＋ηcosδ）．又有平面波方程［5］：U＝U0eikr．令矩孔O點r＝0，把無關的系數并入U0中，可得在矩孔上的光場分布函數為

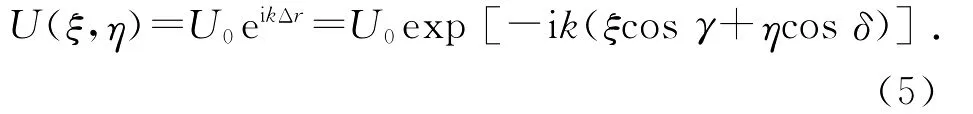
2．3 最終光場分布的計算

將（5）式代入（4）式，經計算，得

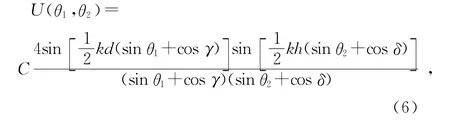
I＝｜U｜2＝

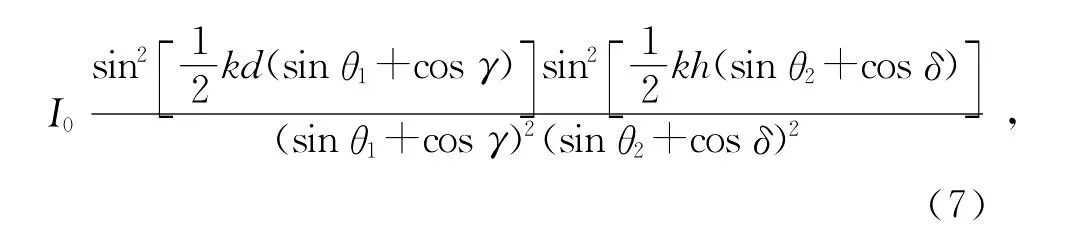
在（6）式中，令γ＝δ＝90°，此時為光線正入射矩孔，（6）式變為

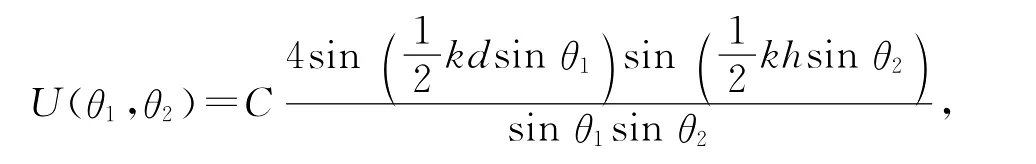
即矩孔正入射時的光場分布［2，4］．所以，（6）式可看作平行光正入射矩孔后光場分．

注意到主極大條紋，滿足sinθ1＋cosγ＝0，sinθ2＋cosδ＝0，即θ1與γ互余，θ2與δ互余，由此可得另一個重要結論：出射光主極大方向與入射光一致，這與實際觀察一致．

3 實驗結果分析及計算機模擬

3．1 光斑在接收屏的分布

利用（6）式和（7）式分析所觀察到的現象．

取較為特殊的例子．令γ＝90°，δ≠90°，作單縫衍射，此時平行光入射方向在ζOη平面內且與η軸有夾角δ，從屏上（接收屏與矩孔平面平行）可以觀察到如圖2現象．由于計算時用矩孔，而矩孔衍射在y方向上也會有光強分布；當變為單縫、多縫或光柵情況時，只需考慮矩孔情況下的在y方向上的主極大，即sinθ2＋cosδ＝0的情況，此時x方向與正入射衍射分布一致，且有

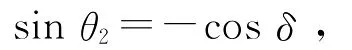
當傾角δ選定后，sinθ2為恒定值．

根據ξOη和x O′y坐標系的定義及兩坐標系和透鏡位置的關系［4］，有

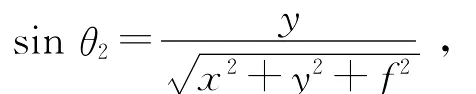
其中，f為薄透鏡的焦距，x為光斑在水平方向延展的距離．對上式變形，得到

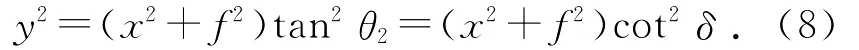
光斑的在接收屏坐標上的分布為雙曲線的形式．

雙曲線的彎曲方向由δ決定：當δ＜90°時，光斑向下彎曲；當δ＞90°時，光斑向上彎曲．假設令δ由90°逐漸向0°變化，在（8）式中，cot2δ逐漸增大，雙曲線曲率增大，與觀察到的現象一致．

3．2 實驗驗證與計算機模擬

設計了如下實驗．裝置如圖3所示，使用632．8 nm氦氖激光器作為光源照射單縫．接收屏與單縫所在平面平行，接收屏上固定坐標紙用以描點讀數．由于激光的準直性很好，實驗中沒有使用透鏡聚焦，而（6）式是利用透鏡來消除透鏡后的光程差，此處不使用透鏡會導致接收屏上分布與（8）式略有不同，但在接收屏與單縫距離較小時，該誤差較小，可忽略．此時（8）式中的f即為單縫和接收屏之間的距離．

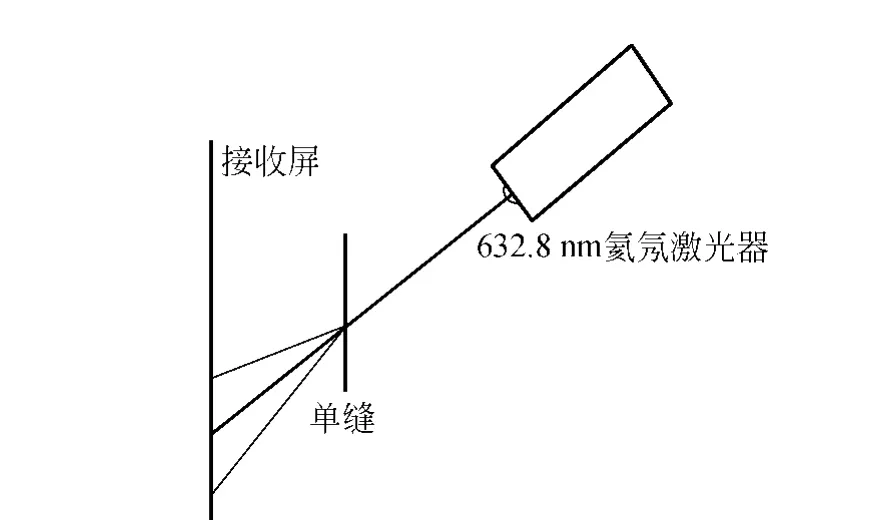
圖3 實驗裝置

衍射光斑在接收屏上的位置分布如圖4所示，利用（8）式，對x2和y2作線性擬合，得到圖5．圖5中，擬合曲線為y2＝72．2＋2．348x2，由（8）式，可得到計算值（cot2δ）cal＝2．348，（f2）cal＝30．750．實驗中測量得到角度δ＝33．5°，f＝5．54 cm，即有實驗值（cot2δ）exp＝2．283，（f2）exp＝30．692，與計算值相差很小，相對誤差分別為2．8%和0．2%．由此可以證明（6）式和（8）式的正確性．

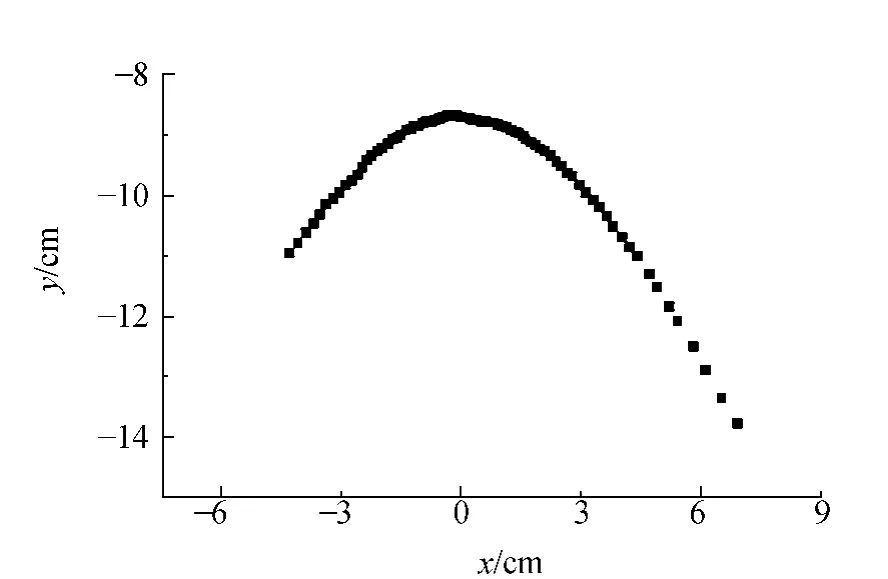
圖4 衍射光斑在接收屏上的位置分布

利用軟件根據（7）式進行單縫衍射光強模擬，得到圖6結果，與圖2對比，光場分布情況一致．其中，模擬參數選擇如下：λ＝632．8 nm，γ＝90°，δ＝60°，f＝10 cm，h＝1 cm，d＝10－4cm，矩孔長寬比為10 000∶1，可看作單縫．

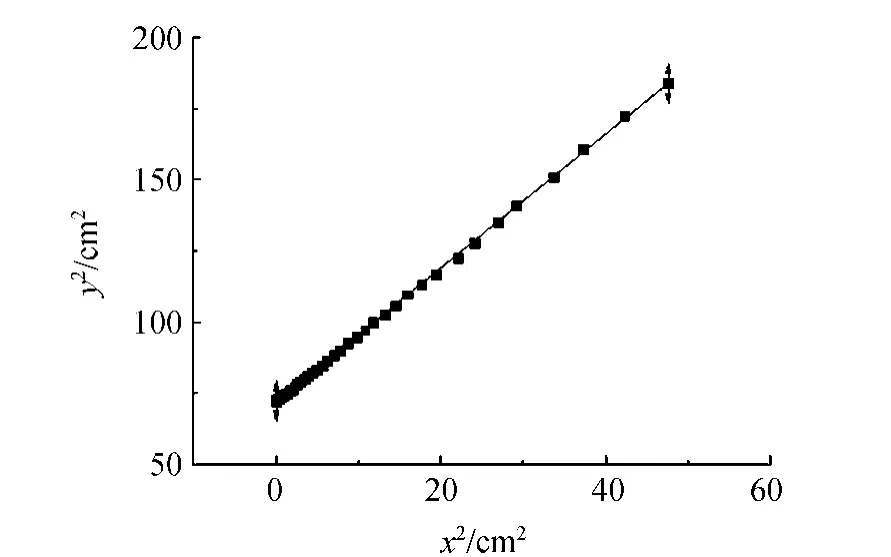
圖5 數據處理與擬合

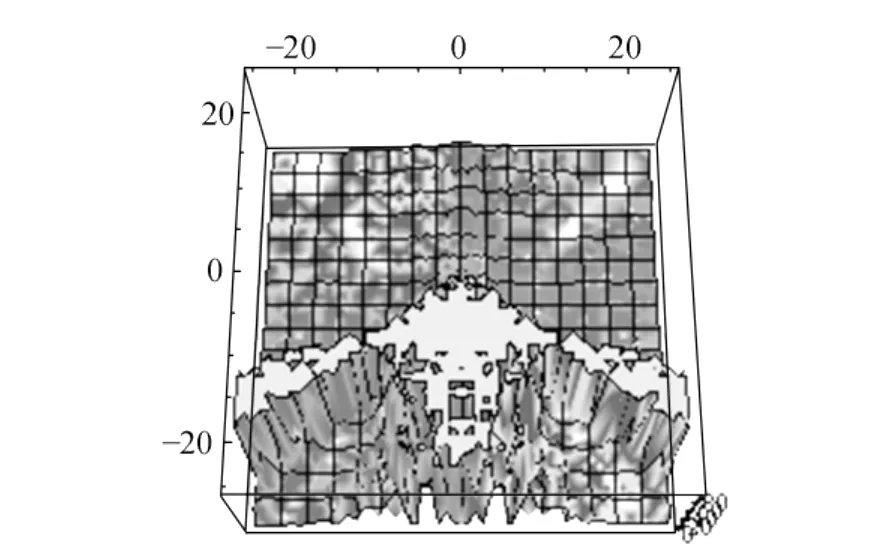
圖6 計算機模擬

4 結束語

本文計算了平行光以任意角度入射矩孔后的光場分布公式［（6）式］，并證明了當接收屏與矩孔（光柵）平行時，光斑分布為雙曲線．（6）式可看作是各類教科書上平行光正入射矩孔情況的推廣．本文通過對光斜入射到光柵上的理論分析和實驗驗證，使得學生對于衍射光柵光柵常量的測定實驗過程當中平行光斜入射產生的實驗現象能夠給予合理的解釋，讓學生了解到更為一般性的衍射現象，掌握了更為普遍性的衍射規律．

［1］ 馬雪梅，張衛平，黃創高，等．基于光柵衍射的實驗分析［J］．大學物理實驗，2010，23（4），34－36．

［2］ 趙凱華．新概念物理教程·光學［M］．北京：高等教育出版社，2004：180－184，199．

［3］ 李芳菊，耿森林，文軍，等．傾斜因子對夫瑯禾費衍射強度的影響［J］．物理實驗，2010，30（10）：33－35．

［4］ 玻恩M，沃耳夫E．光學原理（上冊）［M］．楊葭蓀，等譯．北京：科學出版社，1978：513．

［5］ 平澄，李多，周靜，等．夫瑯禾費衍射自動演示儀［J］．物理實驗，2010，24（4）：12－14．