標準正態分布在積分中的應用

陳志成，張紅云

(河南科技學院數學系，河南新鄉 453003)

1 引言

被積函數為指數函數且原函數不是初等函數的積分問題歷來是積分的難點，它困擾著學習者和工作者.盡管可以部分題目采用極坐標變換，但是計算過程往往比較繁瑣.本文利用標準正態分布的密度函數及性質較系統的解決了該類問題的積分，并對該問題分類給出了相應的積分公式便于記憶和掌握.

2 幾個重要結論

定理1［1－2］若a＞0，則

推論［3］對任意k＞0，則

定理2 若a＞0，x1＜x2，則

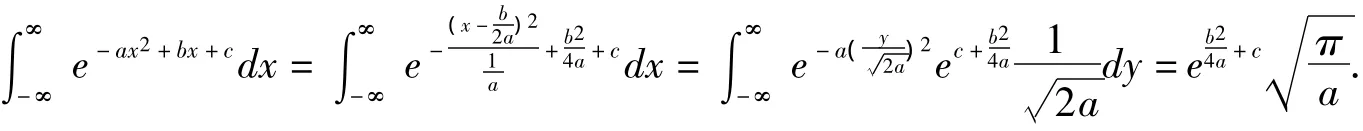
定理4 若a＞0，b，c為實數且x1＜x2，則

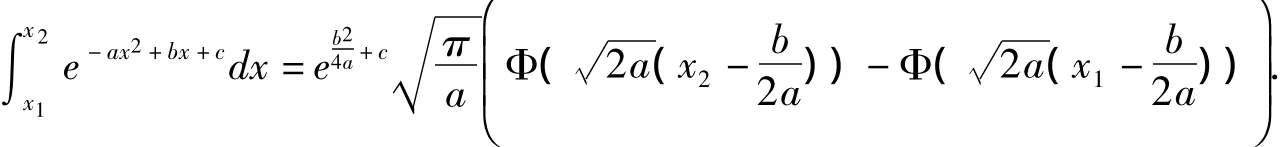
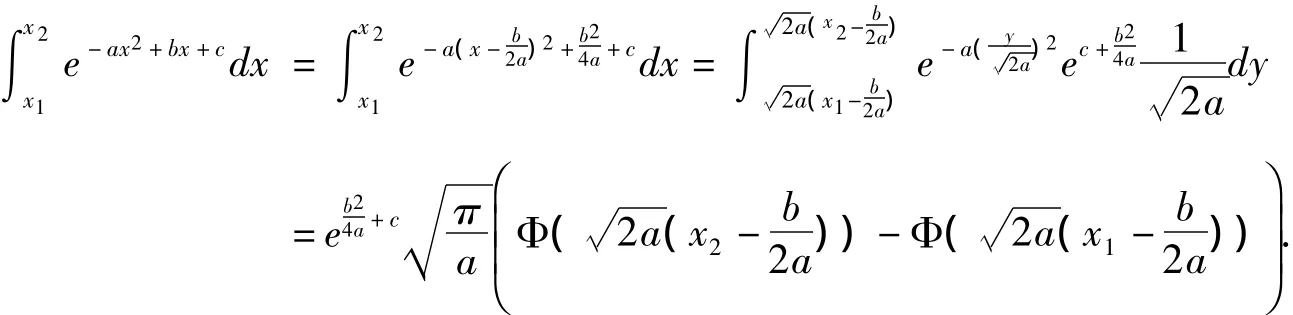
證明:由于被積函數xe－ax2是奇函數且積分區間對稱，則

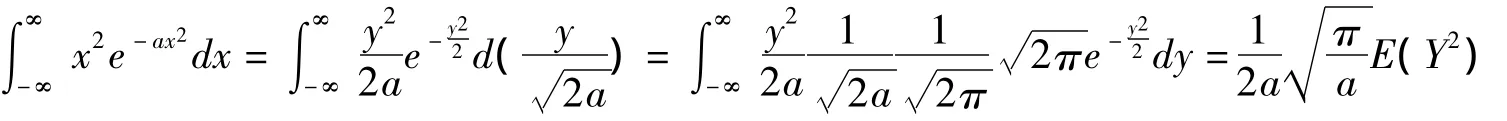
其中Y服從標準正態分布N(0，1)，因而σ2=1，σ2=E(Y2)－(E(Y))2，E(Y)=0，E(Y2)=1.易證

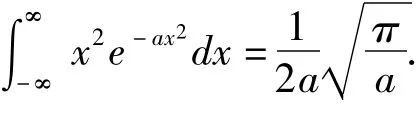
注:本定理通過利用標準正態的相關性質和結論求解，計算過程簡單，思路清晰;相比較而言若利用經常采用的極坐標變換x=r sinθ，y=r cosθ進行求解，需要把一重積分轉化為二重積分，求解過程比較復雜［4］.

定理7 當a＞0，－∞＜k＜∞時，則

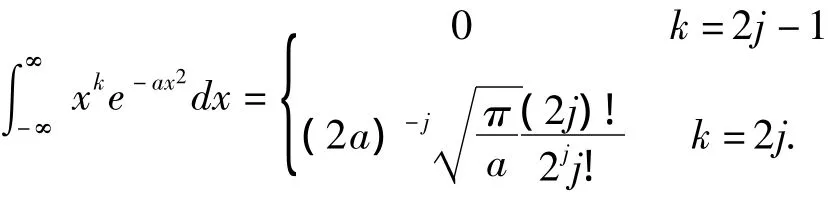
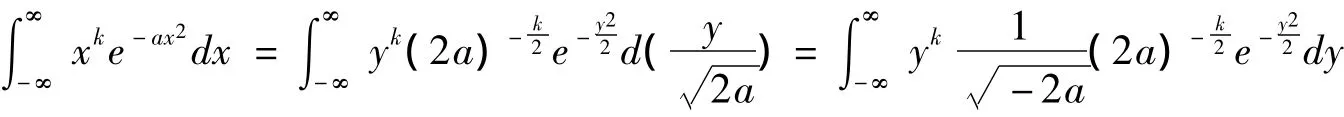
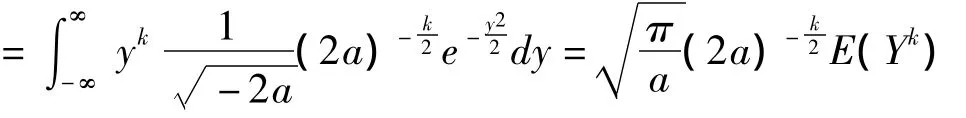
(1)當k是奇數時，顯然E(Yk)=0;

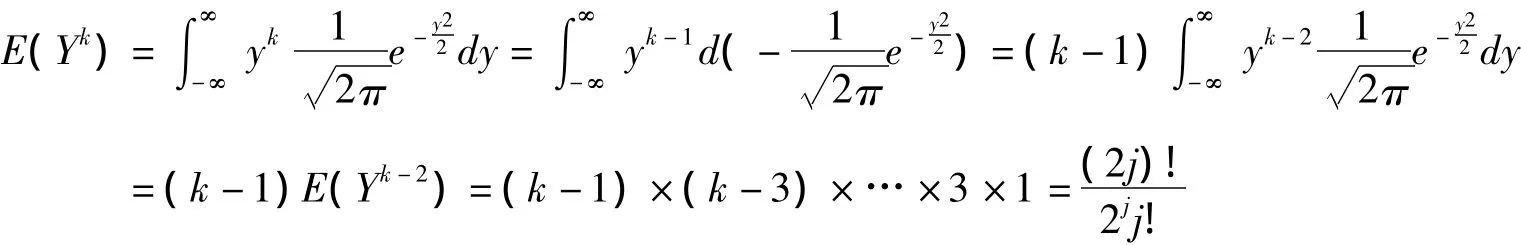
則

［1］盛驟，謝式千，潘乘毅.概率論與數理統計［M］.北京:高等教育出版社，2010.

［2］鄧集賢，楊維權，司徒榮，鄧永錄.概率論及數理統計［M］.北京:高等教育出版社，1988.

［3］李賢平.概率論基礎［M］.北京:高等教育出版社，1997.

［4］孫榮恒.應用概率論［M］.北京:科學出版社，1998.