淺談彈性地基梁的解析法
盧曉莉
(泰山職業技術學院建筑工程系,山東泰安 271000)
在求解軟土地基上結構的靜力問題時,常用方法有解析法、半解析法以及數值解法.解析法屬于精確解法,它的基本思想是分別對結構的控制方程和地基模型的控制方程解析的求解,然后再滿足結構和地基接觸面的位移和應力的連續性條件和結構的邊界條件,即可獲得問題的全部解答.
1 反力直線法
反力直線法[1]是一種近似的方法,該法假定地基反力是按直線規律分布的,其地基反力圖形在對稱荷載作用下是矩形的,在偏心荷載作用下是梯形的,如圖1所示.反力直線法中基礎梁的計算問題是一個靜定問題,根據靜力平衡條件就很容易計算出反力的數值,具有計算簡單方便的優點.由于該方法沒有考慮基礎梁和地基之間的變形協調,因而其計算結果是不準確的,在設計重要的建筑物時不宜采用,通常只在初步估算或設計不太重要的基礎梁的時候使用.

圖1 反力直線法的地基反力假設
2 基于文克爾地基上的初參數法
文克爾地基上的初參數法[2]是一種運用較為廣泛的計算方法,它是通過考慮一受荷載的彈性地基梁的變形情況,取其中一個無窮小的單元,考慮單元的平衡條件,列出平衡方程.同時結合在材料力學中梁受彎的微分公式求出通解,然后根據具體的邊界情況以及受力情況求出內力.例如文克爾地基上的無限長梁的通解為
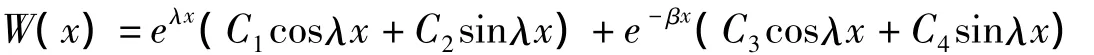
而集中力作用下的無限長梁(如圖2所示),利用邊界條件以及受力情況,最后可得
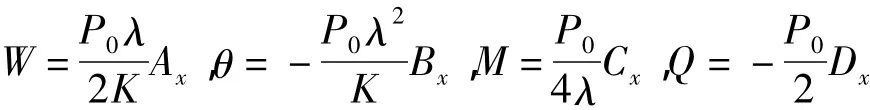
式中
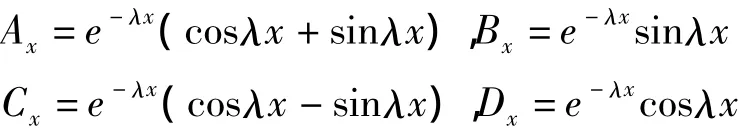
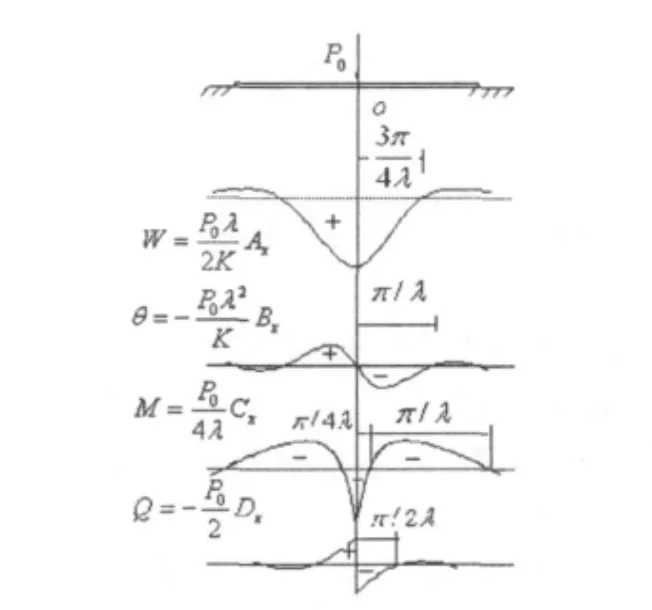
圖2 受集中力作用下文克爾地基上的無限長梁
3 彈性半空間上梁的級數解法
如圖3所示一基礎梁,受到任意分布荷載q(x),基礎反力p(x)沿寬度方向為均布地基上梁的撓曲線微分方程為:
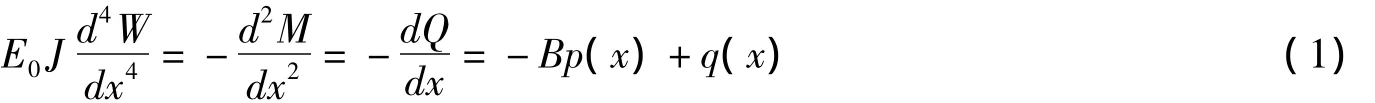
彈性理論平面應力問題的弗拉曼(Flamant)解[3]
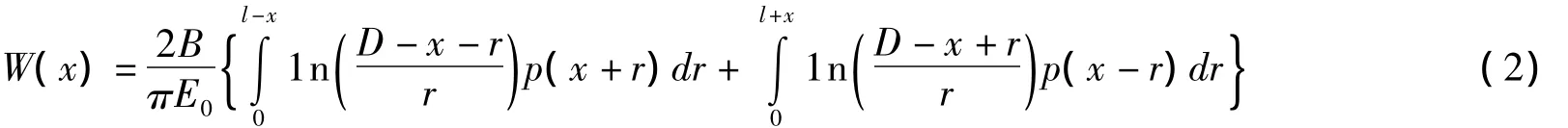
彈性半空間地基表面的豎向位移為:
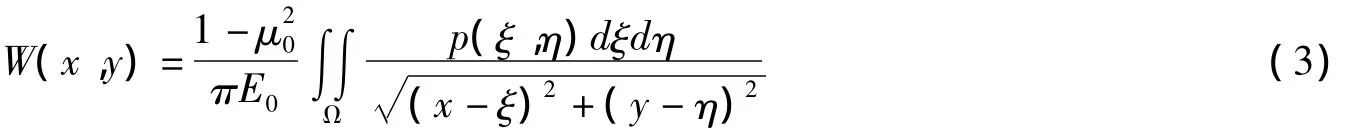
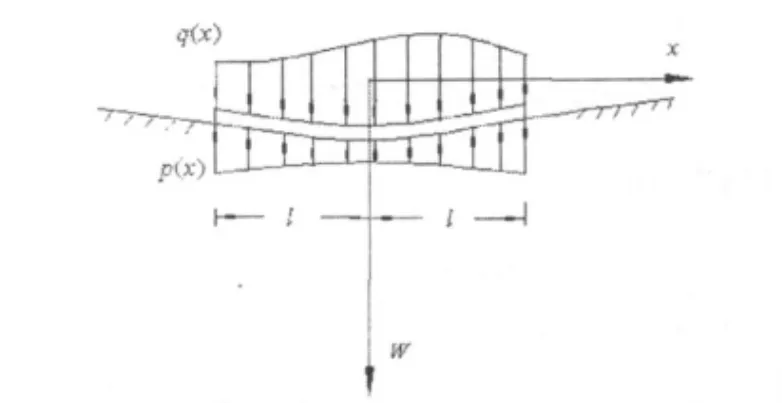
圖3 彈性半平面上的梁
可作為彈性半空間模型在平面應力問題下的特征函數.將式(2)與式(3)代入式(1)則得到不同問題中地基上梁的基本方程.
(1)平面應力問題
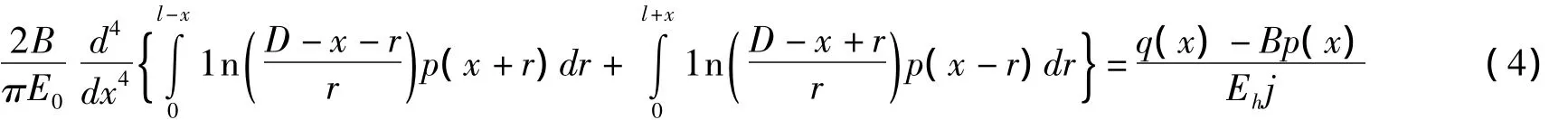
(2)平面應變問題
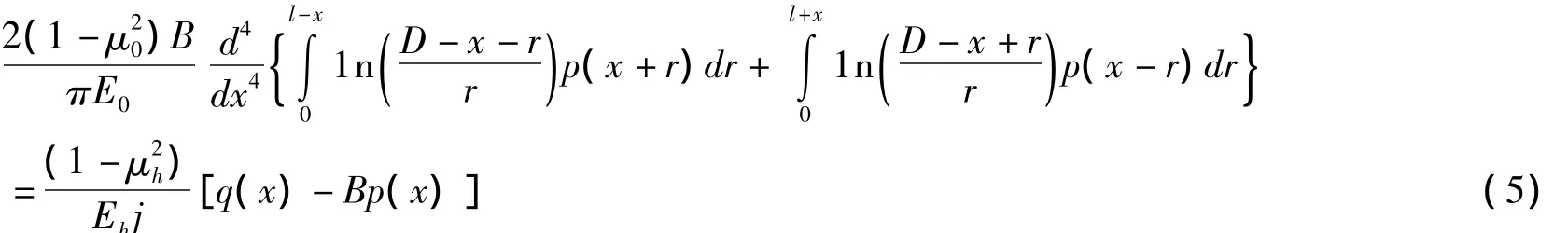
以上兩式中,D為任意選定的參照點的坐標.上述情況下的基本方程都是關于p(x)的微分積分方程,除應滿足梁的邊界條件外,還應滿足靜力平衡條件.
在平衡條件和梁的邊界條件下求解微分積分方程是及其困難的.哥爾布諾夫-彼沙道夫等提出的級數解法有效地解決了這一問題[4],并就若干典型情況給出了大量的內力無量綱計算表格工程設計中不必做復雜的運算,查表后做簡單的量綱換算即可.
級數法的基本思路是先把地基反力p(x)近似地表示為有限項的冪級數:
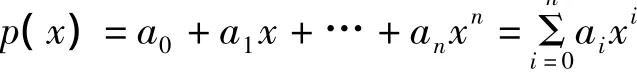
式中ai為n+1個未知的待定系數.由平衡方程可使未知數減少兩個,余下n-1個則通過n-1個點處梁的撓度與地基沉降相等的條件列出n-1個,變形連續方程,因此問題歸結為求解n+1個代數方程.
顯然,當n→∞時,解答是精確的.但實際上這是不可能的,也沒有必要這樣做.當n為有限項時,解答是近似的,如果表格按n=11給出,精度已經相當高,足可以滿足工程需要.
4 小結
本文重點介紹了反力直線法、初參數法、級數解法等具體的解析方法.在前人理論研究的基礎上通過比較,總結出了各種方法適用的地基模型及其各自的優缺點,反力直線具有計算簡單方便的優點.但是另一方面由于該方法沒有考慮基礎梁和地基之間的變形協調,因而其計算結果是不準確的,在設計重要的建筑物時不宜采用.初參數法和級數解法由于要積分,對于簡單結構尚可,但是對于復雜一點的結構計算會相當麻煩,而且不一定能解決.因此,彈性地基上基礎梁的發展方向應該是在解析方法的基礎上加入計算機仿真,這樣既可以節省時間,又可以保證計算精度.
[1]龍馭球.彈性地基梁的計算[M].北京:人民教育出版社,1981.
[2]張子明.用初始函數法計算多層地基的位移和應力[J].巖土工程學報,1986,8(4).
[3]徐芝綸.彈性理論[M].北京:人民教育出版社,1960.
[4]田千里.平面問題彈性地基梁之簡捷解法[J].科學通報,1974,(5).

