分子動力學模擬乙醇/水二元混合物的擴散性質

張翠娟，程岳山

(1.泰山學院材料與化學工程系，山東泰安 271021;2.泰山醫學院化學與化學工程學院，山東泰安 271016)

醇水混合物的結構性質和擴散性質在傳質的理論研究和工業應用方面有重要意義.醇溶解于水時與水形成氫鍵，使二元混合物的性質更加復雜.醇水混合物的性質和相應純物質的性質完全不同［1］.目前，醇的水溶液被廣泛研究，盡管如此，醇的水溶液的物理化學性質仍沒有徹底的解釋清楚［2］.

分子動力學模擬可以研究和預測溶液中的自擴散系數，但相互擴散系數的分子動力學報道很少.計算自擴散系數時可以對每個粒子統計平均，而在計算相互擴散系數時則無法這樣處理，造成相互擴散系數的不確定性較大.目前混合物的擴散系數的研究一般選取簡單氣體混合物為研究對象［3］.

為正確描述流體的性質，分子間相互作用模型的選取十分重要.Jorgensen［4］開發的OPLS模型已經被用于液體醇的熱力學性質.最近，Wenisnk等［5］模擬了醇水混合物的動力學性質，研究中醇采用OPLS模型，水采用TIP4P模型，但作者并沒有研究混合物的性質.本文在全濃度范圍內對乙醇/水二元混合物的擴散性質特別是相互擴散做了研究.

1 模擬的實現

1.1 勢能模型

在模擬中，水采用TIP4P模型［6-7］，該模型比較成熟而且應用廣泛.乙醇分子被認為是剛性結構，有四個相互作用點，即甲基、亞甲基、氧原子和氫原子.在乙醇的分子模型中CH3-CH2-O和CH2-O-H的鍵角分別是108°和108.5°.相關的鍵長見表1.這種簡化的點-點硬球模型最初由Gotlib［8］所采用.

用Lennard-Jones勢來描述不同分子的不同點位之間的相互作用，用庫侖函數描述長程靜電作用，勢能函數形式如下，

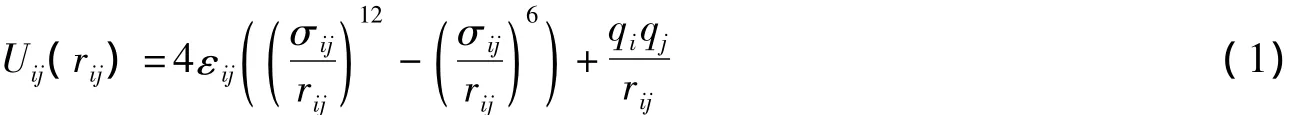
Lennard-Jones勢能和電量參數［8］數值見表2.與OPLS的標準混合規則不同的是，這里不同點位和原子間的相互作用參數采用L-B混合規則.

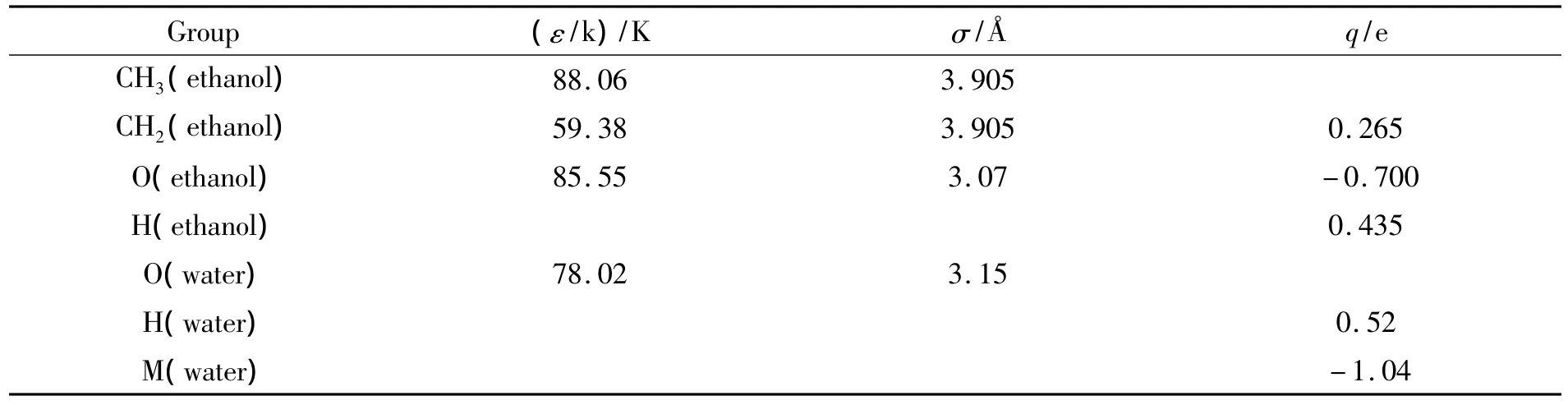
表2 乙醇和水的Lennard-Jones分子間作用參數和庫侖電量

乙醇和水的自擴散系數用兩種方法計算得到:Green-Kubo法(速度自相關函數，VACF)和Einstein方法(均方位移，MSD)［9-10］，

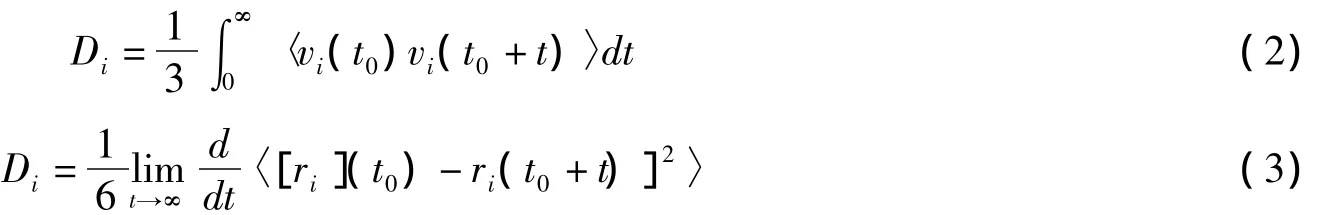
式中vi(t)是分子i在t時刻的質心速度，ri(t)是分子i在t時刻的質心位置.乙醇/水混合物的相互擴散系數可通過計算得到［9，11］

式中D0ij是動力學相互擴散系數，C(t)是相對速度自相關函數(RVCF)，后者被定義為

Jij(t)是一個集體動力學變量，Q是熱力學因子.它們可以用下面的公式計算，

上面的公式中ci是分子i的數密度，Ni是i的分子數目.γi是組分i的活度系數，xi是組分i的摩爾分數.

1.2 模擬方法

對乙醇/水混合物的模擬選取NVT系綜，用Nosé-Hoover算法控制溫度使其保持在298.15K.常壓下混合物的實驗密度數據［12］作為NVT模擬的初始輸入.模擬的分子總數為500個.動力學模擬過程中每個分子都看作是剛性的，分子運動包含了圍繞質心的平動和圍繞質心的轉動.

初始構型的選取為立方模擬盒中粒子隨機分布，在三個方向上應用周期性邊界條件.短程作用的截斷半徑為模擬盒子的邊長的一半.時間步長為0.5fs，模擬的總步數為5105.觀察模擬過程中溫度和總能量的變化，系統在105步后達到動態平衡.后面的結果數據用來計算分析各種性質.

2 模擬結果與討論

2.1 自擴散系數

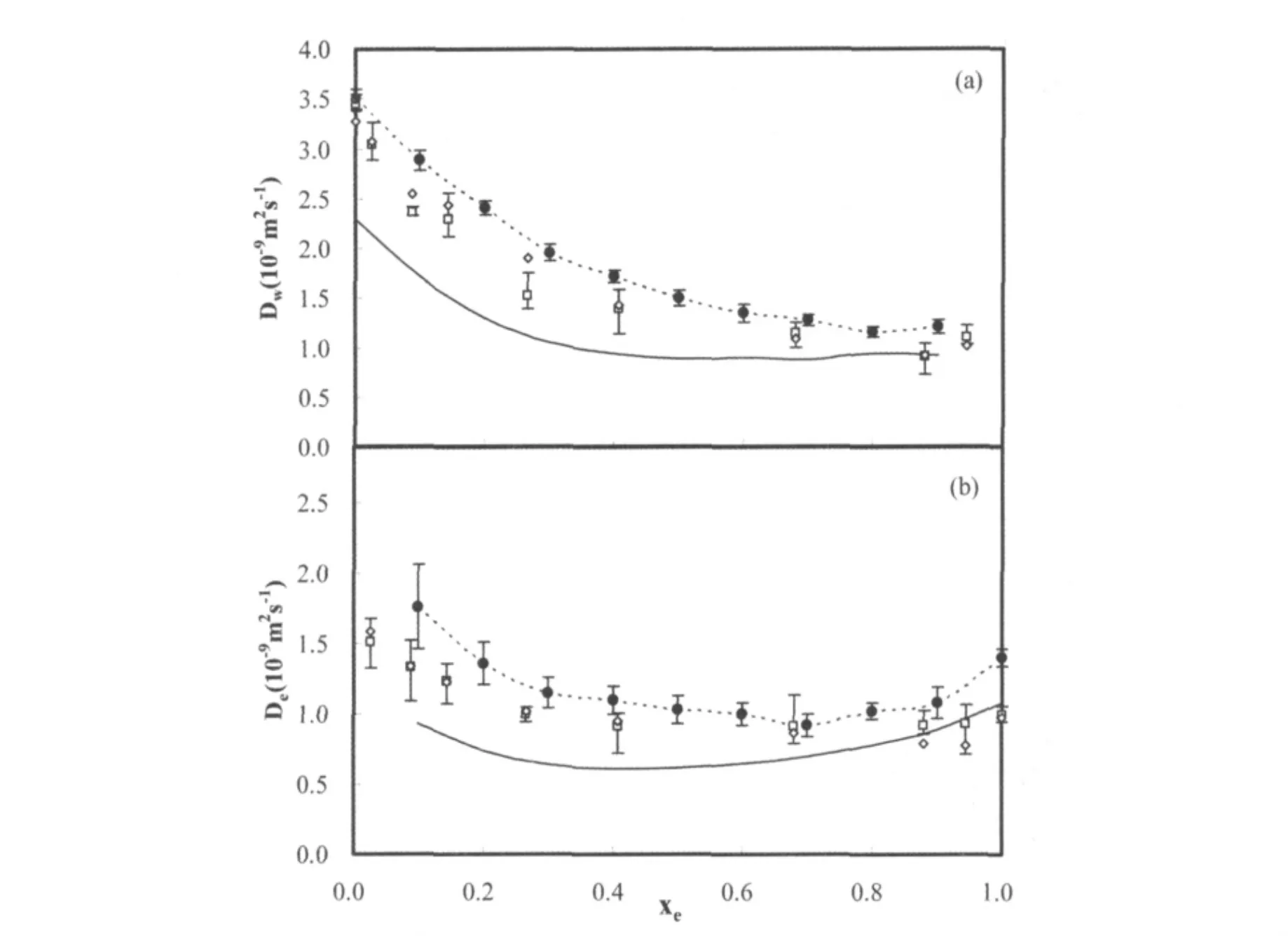
圖1 (a)298.15 K時水在混合物中的自擴散系數.為清晰只畫出了VACF的誤差棒.□:VACF模擬值;◇:MSD模擬值;直線:實驗數據［2］;虛線:文獻的MD模擬值［5］.(b)298.15 K時乙醇在混合物中的自擴散系數□:VACF模擬值;◇:MSD模擬值;直線:實驗數據［13］;虛線:文獻的MD模擬值［5］

我們通過均方位移(MSD)和速度自相關函數(VACF)這兩種方法計算得到的混合物中水的自擴散系數見圖1(a).為了比較計算結果的正確性，我們同時也畫出了實驗數據［2］和相關的文獻模擬數據［5］.可以看出，我們的計算結果比實驗值大，比文獻的模擬結果小.混合物中乙醇的自擴散系數見圖1(b)，實驗數據和相關的文獻模擬數據［5］也同時畫出.前面已經討論過，使用剛性Van Leeuwen模型和OPLS模型所得到的擴散系數的不同，可能是因為采用NVT系綜和NPT系綜的差異造成的.從圖中可以看出，混合物中水和乙醇的自擴散系數隨乙醇濃度的增加，經歷了一個首先降低之后趨于平緩的過程.模擬結果的這種趨勢和實驗值是吻合的.低乙醇濃度時，水和乙醇的自擴散系數降低說明乙醇和水存在比較強的相互作用.在高乙醇濃度時，乙醇和水的自擴散系數和混合物的濃度不相關.這種行為與乙醇分子和水分子在該濃度下的運動的強關聯性相對應.在乙醇濃度較高的情況下，水分子失去了它的網狀氫鍵結構，更易于以單個分子的形式與乙醇分子水合.

水在混合物中的自擴散行為可以用“自由水”和“結合水”來描述［13］.我們沿用Bedrov等人在文獻中提出的方法［13-14］，混合物中自由水和結合水的數目可以通過分子模擬的數據分析得到.在乙醇-水的O-O徑向分布函數的基礎上，認為結合水是位于乙醇分子第一個配位圈之內的水分子.如果水中的氧原子和乙醇的氧原子的距離小于3.5°A，那么這個水分子就被定義為結合在這個乙醇分子上.結合水的分率就是結合水的水分子數目與全部水分子數目的比值.我們計算出該比值隨乙醇濃度的變化，見圖2.從圖中可以看出，結合水的摩爾分率隨著乙醇濃度的增加而增大.在乙醇濃度很高的情況下，絕大多數水分子以結合的形式存在，此時水的自擴散系數與乙醇的關聯性較大.

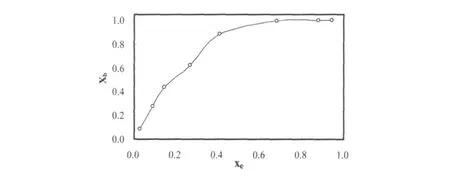
圖2 乙醇/水混合物中由動力學模擬計算得到的束縛水分子的比例

根據上面的分析，水在乙醇-水溶液中的自擴散行為可以表示為兩種擴散行為的貢獻:自由水的貢獻和結合水的貢獻［13-14］.這里Dw

0是純水的自擴散系數，De是混合物中乙醇的自擴散系數.Xb是我們計算得到的結合水的摩爾分率.Kb為結合系數.關聯動力學模擬計算得到的自擴散系數(為了保持圖形清晰，只畫出MSD的結果)和方程8，我們取Kb的最優值為1.24.從圖3中可以看出，方程(8)合理地描述了乙醇-水混合物中體系中水的自擴散系數隨乙醇濃度的變化.

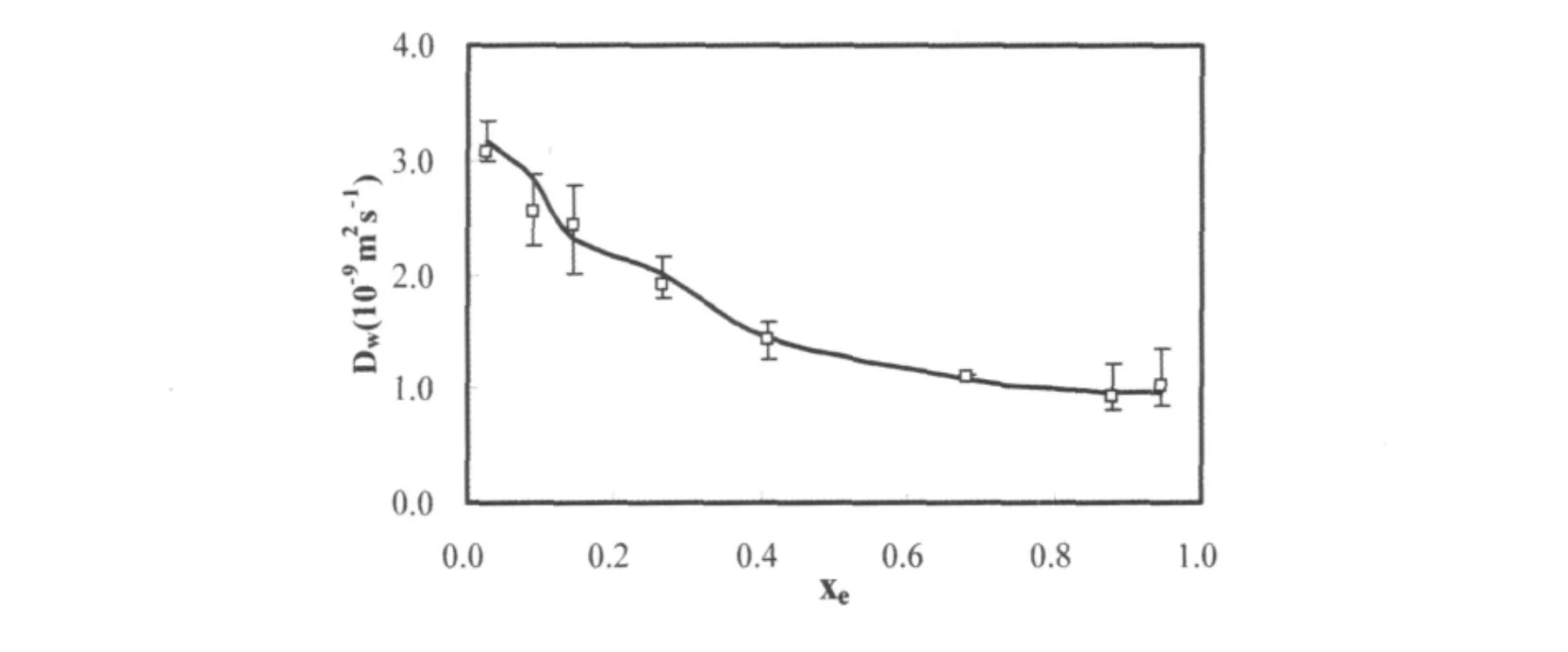
圖3 方程(8)擬合得到的水的自擴散系數隨乙醇濃度的變化

2.2 相互擴散系數

為了得到混合物的相互擴散系數，我們根據方程(5)計算了相對速度自相關函數C(t).混合物的RVCF的震蕩明顯比VACF大的多.與VACF相比［11］，RVCF是一個集體變量并且波動較大，由此根據RVCF計算得到的相互擴散系數(Dwe)與自擴散系數相比，精度較低.一個典型的相對速度自相關函數的積分隨著最大上限積分時間(tmax)的變化見圖4.在圖中可以看出，積分值在10 ps以后趨于穩定，因此我們舍棄10 ps以內的數據，采用的積分值為10到75ps的平均值.

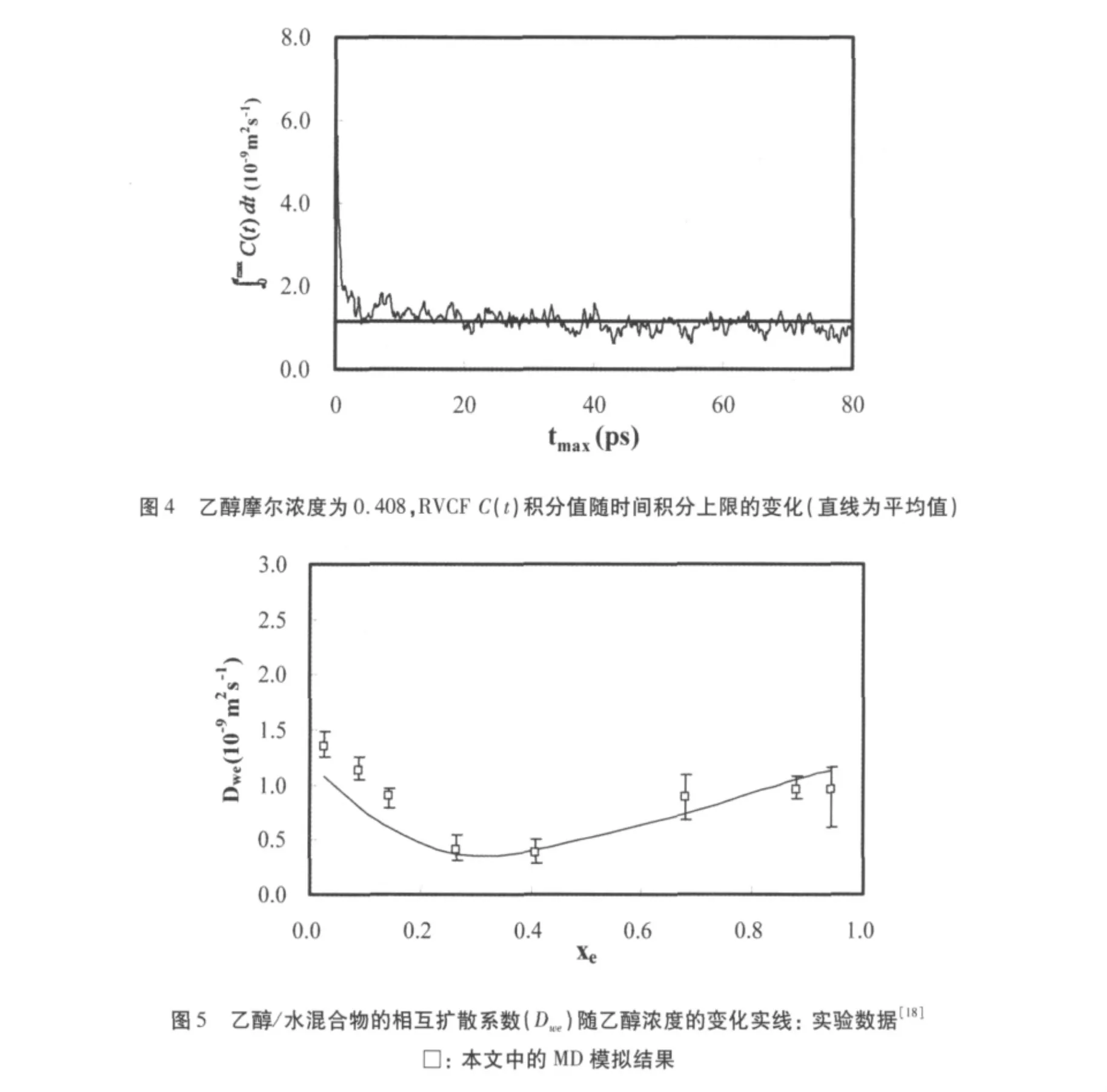
為了得到合理的數據，本文中所有的相互擴散系數都由上述類似程序處理得到.熱力學因子Q可以由不同濃度組成時的化學勢得到.Q可以根據Kirkwood-Buff的理論［15］由分子模擬計算得到，但獲得一個好的統計結果有一定難度［16］.我們采用的熱力學因子的數值是從乙醇-水溶液的汽液相平衡數據計算得到的［17］.全濃度范圍下乙醇-水混合物的相互擴散系數見圖5，實驗數據［18］也在圖中畫出.到目前為止，因為在計算集體性質時存在固有的統計性較差的現象，真實混合物中相互擴散系數的分子動力學研究報道很少.然而，本文中所得到的乙醇-水的相互擴散系數的結果與實驗值相比是令人滿意的.

3 結論

本文采用分子動力學的方法研究乙醇/水混合物的擴散性質.模擬中乙醇分子采用點點剛性模型，水分子采用TIP4P模型.比較不同濃度時乙醇和水的自擴散系數分別與實驗值和文獻的MD模擬值，我們的模擬結果比實驗值稍大.混合物中自擴散系數和混合物的結構有關.水溶液中，水的自擴散系數描述為結合水分子和自由水分子的綜合貢獻.MD模擬得到的乙醇/水混合物相互擴散系數與實驗值十分吻合.計算結果表明，我們采用的乙醇和水的模型對正確描述乙醇/水混合物的結構性質和擴散性質是可行的.

［1］Guàrdia E，MartíJ，PadróJA，etal.Dynamics in Hydrogen Bonded Liquids:Water and Alcohols［J］.JMol Liq，2002，(96-97):3 -17.

［2］Price W S，Ide H，Arata Y.Solution Dynamics in Aqueous Monohydric Alcohol Systems［J］.JPhys Chem A，2003，(107):4784-4789.

［3］Zhou J，Lu X H，Wang Y R，et al.A Molecular Dynamics Simulation of Infinite Dilute Diffution Coefficients of Benzene and Naphthalene in Supercritical Carbon Dioxide［J］.Chem Jof Chinese Universities，2000，(21):762-765.

［4］Jorgensen W L.Optimized Intermolecular Potential Functions Liquid Alcohols［J］.JPhys Chem，1986，(90):1276-1284.

［5］Wenisnk E JW，Hoffmann A C，Maaren P J，etal.Dynamic Properties ofWater/ElcoholMixtures by Computer Simulation［J］.JChem Phys，2003，(119):7308-7317.

［6］Jorgensen W L，Chandrasekhar J，Madura JD，etal.Comparison of Simple Potential Functions for Simulating Liquid Water［J］.JChem Phys，1983，(79):926-935.

［7］Chialvo A A，Cummings P T.Microstructure of Ambient and SupercriticalWater.Direct Comparison between Simulation and Neutron Scattering［J］.JPhys Chem，1996，(100):1309-1316.

［8］Gotlib IY，Piotrovskaya EM.Properties of Coexisting Phases for the Ethanol-Ethane Binary System by Computer Simulation［J］.J Phys Chem B，1999，(103):7681-7686.

［9］Stoker JM，Rowley R L.Molecular Dynamics Simulation of Real-Fluid Mutual Diffusion Coefficientswith the Lennard-Jones Potential Model［J］.JChem Phys，1989，(91):3670-3676.

［10］Zhou Y，Miller G H.Green-Kubo Formulas for Mutual Diffusion Coefficients in Multicomponent Systems［J］.JPhys Chem，1996，(100):5516-5524.

［11］Kamala CR，Ayappa K G，Yashonath S.Mutual Diffusion in A Binary Ar-Kr Mixture Confined within Zeolite NaY［J］.Phys Rev E，2002，(65):1-12.

［12］Easteal A J，Woolf L A.Pressure and Temperature Dependence of Tracer Diffusion Coefficients ofMethanol，Ethanol，Acetonitrile，and Formamide in Water［J］.JPhys Chem，1985，(89):1066-1069.

［13］Bedrov D，Borodin O，Smith GD.Molecular Dynamics Simulation of1，2-DimethoxyethaneWater Solutions.2.Dynamical Properties［J］.JPhys Chem B，1998，(102):9565-9570.

［14］Borodin O，Bedrov D，Smith GD.Concentration Dependence ofWater Dynamics in Poly(Ethylene Oxide)Water Solutions from Molecular Dynamics Simulations［J］.JPhys Chem B，2002，(106):5194-5199.

［15］Kato T.Determination of Velocity Correlation Coefficients in Aqueous Solutions of2-butoxyethanol by Quasi-elastic Light Scattering，Pulsed-gradient FT-NMR，and Rayleigh-Brillouin Scattering［J］.JPhys Chem，1985，(89):5750-5755.

［16］Kataoka Y.The Concentration Fluctuations and the Mutual Diffusion Coefficient in the Supercritical Solution［J］.JMol Liq，2001，(90):35-43.

［17］Yang X N，Wang R S.Correlation and Prediction of Liquid Diffusion Coefficients in Binary Systems［J］.Chinese J of Chem Eng，1996，(4):104-111.

［18］Tyn M T，CalusW F.Temperature and Concentration Dependence of Diffusion Coefficients of Some Binary Liquid Systems［J］.JChem Eng Data，1975，(20):310-316.