富寧縣城鎮體系空間結構及水系的分形研究

丁賢法

(文山學院生化系，文山云南663000)

分形是城鎮體系有效占據空間的重要形式，分形幾何理論及其技術已成為通過局部認識整體、從有限認識無限的一種新工具，對地學等自然科學與社會科學都產生了很大的影響，常用來研究形態極不規則的地貌、等高線、水系、斷層以及預測地震、水旱等自然災害等。由于社會經濟系統內在的自組織演化以及外在地形、水系等的制約，城鎮體系普遍具有分形特征。文章應用GIS數字化了云南省富寧縣的掃描地圖，計算了該縣13個城鎮的聚集分維與空間關聯分維，同時計算了富寧縣那馬河水系的分維，并討論了各種分維對該縣城鎮化發展的意義。

1 富寧縣城鎮體系聚集分維研究

假設區域的城鎮體系各要素按自相似原則圍繞中心城市或首位城市呈凝聚態分布，如果距首位城市平均半徑Rs與相應的城鎮個數S滿足關系:

則區域城鎮的分布是分形的，其計算方法陳濤［1］已作了介紹，其中D為分維，D值反映了城鎮圍繞中心城市隨機聚集的特征。當D＜2時，說明城鎮分布從中心城市向周圍腹地是密度衰減的，中心城市的中心性作用很強;當D=2時，城鎮分布在半徑方向上是均勻變化的;當D＞2時，說明城鎮分布從中心城市向四周是密度遞增的，說明中心城市不具備中心性作用，整個體系呈離心狀態。

應用MapInfo測量出新華鎮至其他城鎮的直線距離ri(單位:km，見表1)，計算出富寧縣城鎮體系的隨機聚集分維D=1/0.734 6=1.361 2＜2(見圖1)，說明新華鎮作為富寧縣的政治、經濟、文化中心，其中心作用較強，城鎮體系要素密度由該鎮向四周衰減;新華鎮還是滇東南的交通樞紐，有323國道與衡昆高速公路經過，規劃目標為:發展生物制品加工和旅游服務、物資集散等第三產業為主，具有壯族民族風情特色的山水城市。觀察富寧縣城鎮體系空間結構的隨機聚集分維可知，除里達鎮略偏離直線外，各鄉鎮幾乎位于一條直線上，說明目前該縣城鎮體系的空間結構已趨于最優化的分形結構。

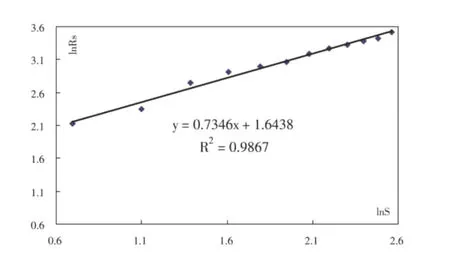
圖1 富寧縣城鎮體系的隨機聚集分維

表1 富寧縣城鎮分布的重心距和平均半徑

2 富寧縣城鎮體系的空間關聯分維研究

2.1 城鎮體系的空間關聯分維計算方法

城鎮體系的空間關聯函數C(r)定義為

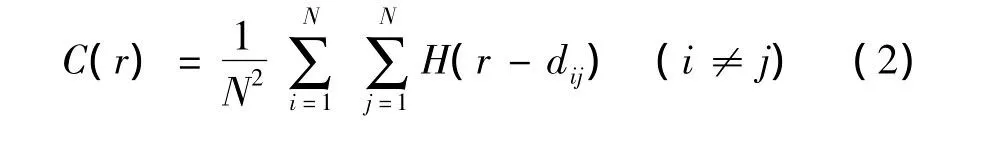
式中N為區域內城鎮數目，r為碼尺(yardstick)，dij為i、j兩城鎮的歐氏直線距離，即烏鴉距離(crow distance)，H為Heaviside函數，具有以下性質:

為了計算方便，通常將C(r)改為

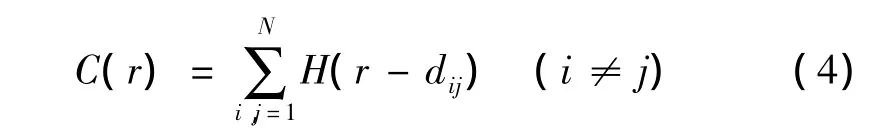
如果城鎮體系的空間分布是分形的，則應具有標度不變性，即

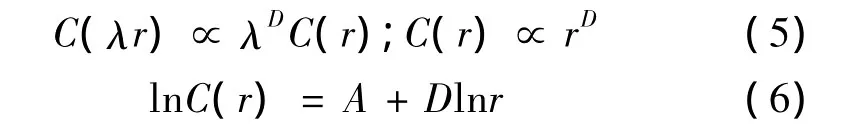
λ為尺度比，D為城鎮體系的空間關聯維數。D一般在0～2之間變動，當D→0時，表明城鎮分布高度集中于一地，形成一個首位城市，但是這種情況很少出現;當D→1時，表明城鎮體系各要素集中到一條地理線(如河流、公路、海岸等)上;當D→2時，表明城鎮空間分布很均勻。將dij改為實際交通里程，即乳牛距離(cow distance)時，可得城鎮交通網絡的關聯維數D' 。D' 一般在0～2之間變化，D' 越小，表示城鎮之間聯系越緊密，城鎮分布趨于集中;D' 越大，城鎮之間相互聯系越弱，趨于均勻分布。定義網絡直通度(又稱牛鴉維數比)為:ρ=D' /D，當ρ＜0.5或ρ＞1時，表明城市之間的網絡連通性較差;當0.5＜ρ＜1時，表明城市之間的網絡連通性較好;當ρ接近于1，表明城市之間交通趨于直線式通車，ρ=1為極限值［2］。

2.2 富寧縣城鎮體系的空間關聯分維

用MapInfo測量了富寧縣13個城鎮之間的直線距離，形成一個13×13的矩陣(見表2)，取步長為8 km對其進行篩選，得到一系列點對(r，C(r))(見表3)，將其標繪在雙對數坐標圖內，進行線性回歸計算，發現圖中存在明顯的無標度區(圖2)，對無標度區的點列進行回歸運算，得到D=1.297 7，測定系數R2=0.998 3，說明城鎮體系趨于線性分布。同理，將表2的直線距離改為交通里程，得到公路交通網絡的分維數為D' =1.032 8，測定系數R2=0.994 5。D' 較大，說明城鎮之間聯系不夠緊密;網絡直通度為ρ=D' /D=0.796，說明富寧縣城鎮之間網絡聯接較好，但有待改進與提高，其主要原因是由于北部鄉鎮之間缺乏聯接，如阿用鄉與那能鄉直線距離只有31.6 km，卻需繞道縣城，交通里程達144.6 km。目前，兩地之間正在建設一條縣級道路。由于323國道與衡陽至昆明高速公路經過，富寧縣交通網是比較發達的。

富寧縣位于云南省最東部，是云南省通往廣西北部灣的公路出海大通道。廣西百色水利樞紐竣工后，這里形成了約300 km的優良航道，位于那馬河右岸、甲村河左岸河段的富寧港已動工，可沿右江、珠江至港澳，將成為云南省的水路出海通道。

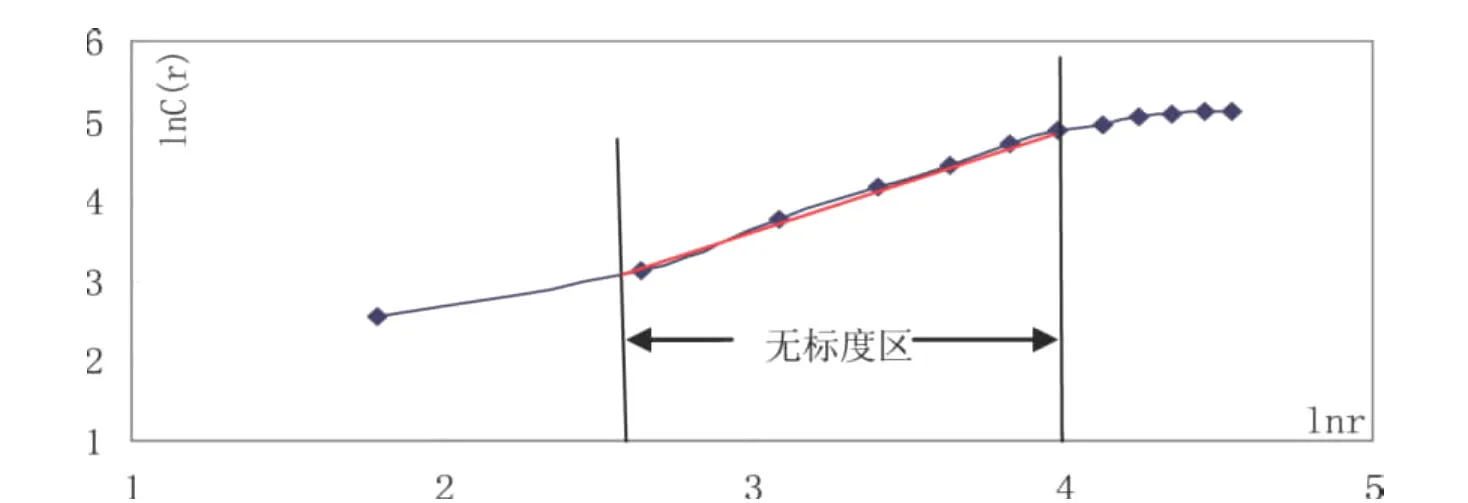
圖2 富寧縣城鎮體系的空間關聯分維

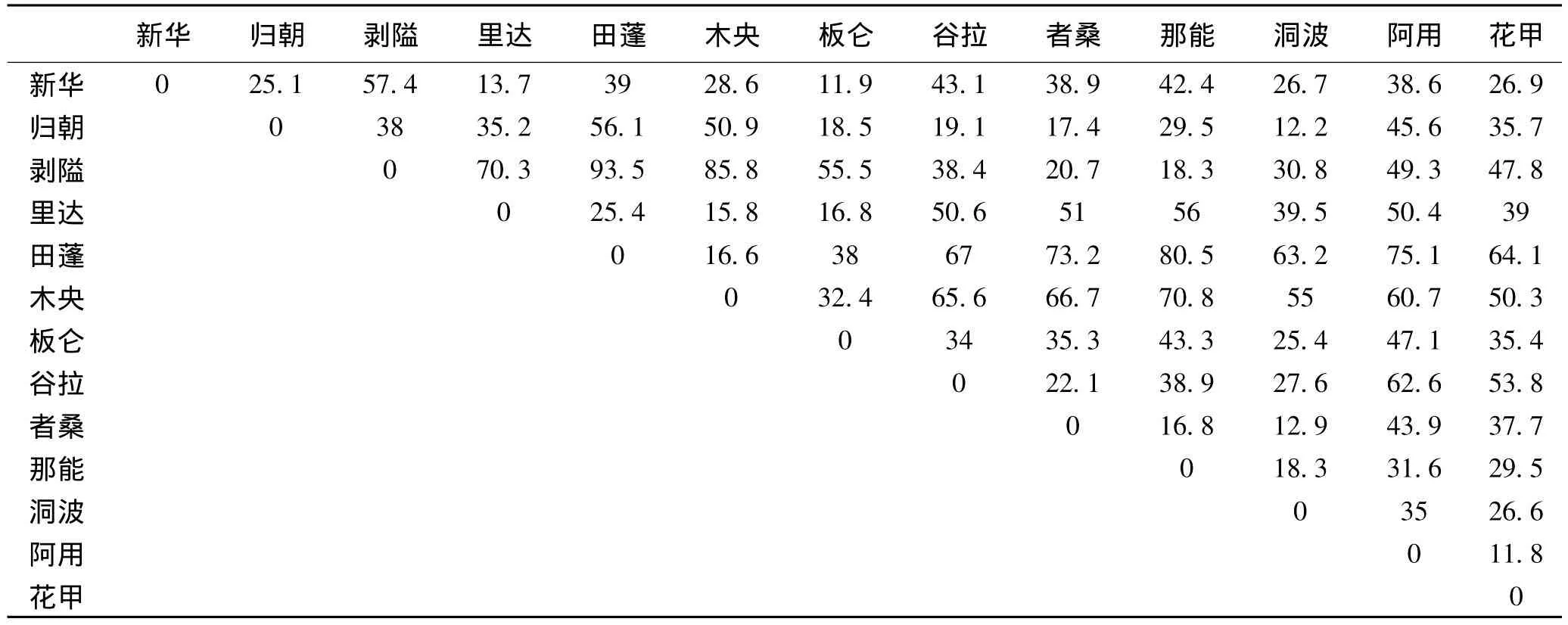
表2 富寧縣13個城鎮之間的直線距離(單位:km)

3 那馬河水系的分維

水系具有典型的分形構造，城鎮選址大都受到水系的制約。富寧縣水資源豐富，喀斯特地貌發育，水系發達，絕大多數城鎮位于水系附近。選取那馬河水系，計算其分維。那馬河流域干支流水系均位于富寧縣境內，且已動工建設的富寧港即位于此。應用MapInfo數字化了該流域水系，輸出為AutoCad的 dxf格式［3］，在 ArcView GIS［4］中按一定尺寸(ε，單位:km)將其轉為網格(N(ε))，得到表4，計算出其分維為D=1.102 1(見圖3)。

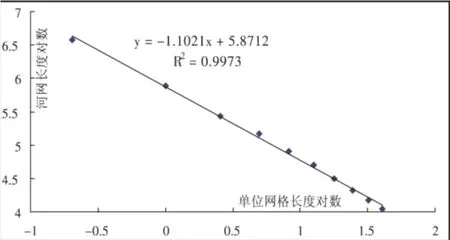
圖3 那馬河水系的分維值

表4 那馬河水系的分維值計算

據何隆華等［5］的研究，當水系的分維≤1.6時，流域地貌處于侵蝕發育階段的幼年期(美國地貌學家戴維斯于19世紀末提出地貌侵蝕循環理論，將流水地表的發育分為幼年期、壯年期和老年期)，水系尚未充分發育，河網密度小，地面比較完整，河流深切侵蝕劇烈，河谷呈V形，這與實際觀測較一致。

4 結論與討論

基于GIS與分形理論，計算了富寧縣城鎮體系空間結構的聚集分維與關聯分維，顯示新華鎮的中心作用較強，城鎮化發展處于極核階段，在整體上以新華鎮為中心的空間結構已趨于最優化的分形結構;受山地地形的制約，富寧縣城鎮體系趨于線狀地理要素分布，主要為公路與河流，文山州［6］、丘北縣［7］等城鎮體系的空間分布在整體上與此相似。分形研究的結果還顯示富寧縣交通網絡聯接較好，那馬河水系的分維顯示其地形發育處于地貌學家戴維斯提出的侵蝕循環的幼年期。

2006年底，富寧縣農業人口占總人口的比例高達93.0%，城鎮化水平低，境內山高坡陡，地勢狹窄，山區面積占96%，石山區又占山區面積的三分之一，土地資源極為寶貴。因此受地形的制約，“點－軸”系統模式應是統籌城鄉一體化發展的最佳空間模式［8－9］，這里的“點”指各級城鎮，“軸”指聯結點的線狀基礎設施，主要包括交通干線、高壓輸電線、通訊線路、供水線路等工程性線路，在城鎮的空間拓展、行政區劃調整、異地扶貧搬遷中，宜向交通干線、河流聚集，以擴大和發揮城鎮的集約與規模效應。例如以323國道與衡昆高速公路沿線為主軸，西部以新華鎮為中心，中部以歸朝鎮為中心，東部以剝隘鎮為中心，由主軸線向南北兩翼，可劃分出若干二級發展軸，特別是新華鎮－里達鎮－木央－田蓬鎮沿線，田蓬鎮規劃為富寧縣城南部區域性中心城鎮，是省二級口岸，以發展邊境旅游、邊貿為主的邊境小城鎮，可達越南河內、海防，但由于受到西部河口、天保等國家級口岸的空間競爭影響，這條道路等級較低。另外，由于缺乏鐵路運輸，與同位于東部但位置偏西的曲靖市富源縣相比，富寧縣還未充分發揮云南省東大門的區位優勢，這一局面有望在云桂鐵路建成后改變。

最后，由于富寧縣地貌發育處于侵蝕循環的幼年期，受山地地形制約，在很長的時間內，城鎮化發展都需遵循“點軸”模式。由于鄉鎮聚落體系與城市體系遵循相同的分形模式［10］，可進一步應用分形研究該縣村－鎮體系的分形特征。另一方面，地質構造運動可能活躍，需注意防范地震、崩塌、滑坡、泥石流等自然災害。由于自然災害的發生在時間軸上表現為一系列的點狀事件，類似于分形幾何中的康托爾集合(cantor)，因此可以根據歷史統計資料，用分形來預測該縣未來自然災害的發生時間和趨勢［11］。

［1］陳濤．城鎮體系隨機聚集的分形研究［J］．科技通報，1995，(2):98 －101．

［2］丁賢法．基于分形理論的云南省文山州城鎮體系研究［J］．小城鎮建設，2008，(8):101 －103．

［3］朱曉華，查勇．MapInfo與ArcView GIS軟件在線體分形分析中的應用［J］．測繪信息與工程，2002，(5):4 －5．

［4］丁賢法．基于ArcView的文山州系列地圖制作研究［J］．文山師范高等專科學校學報，2006，(4):92－94．

［5］何隆華，趙宏．水系的分形維數及其含義［J］．地理科學，1996，(2):124 －128．

［6］丁賢法，李巧媛．云南省文山州城鎮體系空間結構的分形研究［J］．國土與自然資源研究，2010，(2):20－21．

［7］丁賢法，沐建華，許聯芳等．基于Map Info的丘北縣城鎮分形與辣椒產業發展研究［J］．安徽農業科學，2008，(23):10109－10111。

［8］陸大道．論區域的最佳結構與最佳發展——提出“點－軸系統”和“T”型結構以來的回顧與再分析［J］．地理學報，2001，(2):127 －135．

［9］劉繼生，陳彥光，劉志剛．點－軸系統的分形結構及其空間復雜性探討［J］．地理研究，2003，(4):447－454．

［10］單偉東，陳彥光．信陽地區城鄉聚落體系的分形幾何特征［J］．地域研究與開發，1998，(3):48～64．

［11］丁賢法，李巧媛，胡國賢．云南省近500年旱澇災害時間序列的分形研究［J］．災害學，2010，(2):76 －80．