高師數(shù)學專業(yè)開設《幾何畫板》課的必要性研究

王奮平

(瓊州學院理工學院，海南三亞572022)

《幾何畫板》作為一種具有學習容易，操作簡單，功能強大的的教育軟件，是由美國Key Curriculum Press公司制作并出版的優(yōu)秀教育軟件，1996年該公司授權人民教育出版社在中國發(fā)行該軟件的中文版。也是全國中小學計算機教育研究中心在CAI(Computer Assistant Instruction)中推廣使用的軟件之一，可用在平面幾何、平面解析幾何、射影幾何、代數(shù)與函數(shù)、向量、微積分等數(shù)學內(nèi)容的學習和教學中，可以方便、快捷地開發(fā)出具有實用性的課件;不僅如此，它簡單易學，易被掌握，花費較短時間就可以獨立制作數(shù)學課件，應用于課堂教學，方便快捷，受到廣大中小學數(shù)學教師的普遍歡迎.

1 幾何畫板在中學數(shù)學教學中的作用

1.1 使得抽象數(shù)學形象化，有利于提高教學效率利用《幾何畫板》的動態(tài)功能可以清楚地展示函數(shù)圖形、幾何圖形中無法用模具、板書圖形描述的性質(zhì)，例如:“旋轉(zhuǎn)體”之一的圓柱體教學中課本敘述:“圓柱可以看成是矩形以它的一邊所在直線為軸，其余各邊旋轉(zhuǎn)一周而成的面所圍成的幾何體。”這一抽象的敘述使學生感到困惑，難以理解，因為看不見又摸不著。而教師利用靜止的幾何圖形又進不清楚。《幾何畫板》給圓柱體的概念教學提供了現(xiàn)代化的手段。用“跟蹤”、“移動”等功能，動態(tài)地顯示了圓柱展開成為一個矩形的過程，直觀地展示了所圍成的曲面。同時可看到矩形的另兩邊通過旋轉(zhuǎn)所形成的平面圓。此過程可分開演示，最后合成演示。這樣動畫演示使得以往講不清的概念現(xiàn)在講清了，抽象的知識形象化了，靜態(tài)的知識動態(tài)化了。減少了課堂上的抽象費時的講解，為學生觀察現(xiàn)象，發(fā)現(xiàn)結論，探討問題創(chuàng)設了較好的“情景”不僅使學生便于理解，而且給學生提供了一個輕松愉快的氛圍。用“移動”命令可以實現(xiàn)三棱柱分解為三個三棱錐的形象動畫過程，使得相對復雜的圖像變換過程簡單易懂。

1.2 有利于開展探究性教學《幾何畫板》的圖形對應點的可移動性可以展示代數(shù)、幾何性質(zhì)。例如:在復平面內(nèi)作出兩個復數(shù)的和的平行四邊形圖形，然后拖動實部或虛部的對應點，相應的兩個復數(shù)也發(fā)生了變化，可以看到兩個復數(shù)對應的位置向量也隨之變換位置，但無論如何變換實部、虛部位置，四邊形兩組對邊仍然保持平行，學生由此可體會到平行四邊形法則的本質(zhì)。運用幾何畫板可以準確有效地驗證代數(shù)、幾何的很多定理、性質(zhì)等，例如:可以嚴整三角形的內(nèi)心、外心、垂心、旁心等幾何點，還可以驗證三角形內(nèi)角和定理、勾股定理、圓冪定理、相交弦定理、圓周角定理、正弦定理、余弦定理、三垂線定理等，通過鼓勵學生自己操作也可以完成上述任務;也可以幾何畫板為工具進行數(shù)學問題的深入研究。例如:在不等式組形成的線性規(guī)劃問題中，可以移動直線在可行域中探求最值，找到最佳值。還可以在拋物線的繪制過程中通過改變系數(shù)，如在講函數(shù)y=Asin(ωx+φ)的圖象時，傳統(tǒng)教學只能將A、ω、φ代入有限個值，觀察各種情況時的函數(shù)圖象之間的關系，而利用《幾何畫板》則可以以三條線段的長度或坐標分別代表A、ω、φ的值，作出y=Asin(ωx+φ)圖后，當拖動上述三條線段的某一端點時分別改變?nèi)呛瘮?shù)的振幅、周期和相位，這樣在教學時既快速靈活，又不失一般性。還可以在同一個坐標系中作出多個函數(shù)的圖象，如在同一個直角坐標系中作出函數(shù)y=x2、y=x3和y=x1/2的圖象，比較各圖象的形狀和位置，歸納冪函數(shù)的性質(zhì)。用《幾何畫板》還可以探究圖形性質(zhì)的不變性:當幾個不同對象在某些方面(如特征、屬性、關系等)有類同之處，可引導學生合理地聯(lián)想其他方面也有類同之處，利用變式探索、挖掘、概括、引申獲得問題的一般性結果，使特殊問題一般化，零散知識規(guī)律化.借助《幾何畫板》，可以幫助學生發(fā)現(xiàn)數(shù)學性質(zhì)和規(guī)律，體驗“觀察—歸納—猜想—驗證”的數(shù)學過程.

1.3 有利于學生進行自主研究性學習《幾何畫板》也是一個動態(tài)討論問題的工具，對發(fā)展學生的思維能力、開發(fā)智力、促進素質(zhì)教育有著不可忽視的作用，因為幾何畫板的簡單易學，學生可以在教師的指導下很快掌握它的基本功能，經(jīng)過短暫訓練就可以運用《幾何畫板》進行數(shù)學學習，不再有老師滔滔不絕地講，代之以學生動手“做數(shù)學”，老師負責學習的組織，指導學生研究問題，幫助學生學習，成為學生學習的幫助者，學生成為學習的主人。師生可以用《幾何畫板》為工具共同探討數(shù)學問題，探求未知的結論，可以開闊思路，培養(yǎng)能力，提高數(shù)學素養(yǎng)。例如:在學習指數(shù)函數(shù)與對數(shù)函數(shù)的概念后，有學生問到當a＞1時，指數(shù)函數(shù)y=ax與對數(shù)函數(shù)的圖像是否會相交的問題，因為從課本及其它很多參考書上所給的在同一坐標系內(nèi)指數(shù)函數(shù)y=ax與對數(shù)函數(shù)的圖像看，當a＞1時，似乎是不相交的，正確的結論究竟是怎樣?如果讓學生利用《幾何畫板》在同一坐標系作出函數(shù)y=ax和的圖像，底數(shù)a是可以變化的。當0＜a＜1時，學生通過圖像很容易觀察出函數(shù)y=ax與的圖像有且只有一個公共點;當a＞1時，結論是怎樣的呢?當a＞1時，通過拖動線段AB上的點a可以發(fā)現(xiàn)當a＞1.45時，兩函數(shù)圖像沒有交點，當1＜a＜1.45時，兩函數(shù)圖像有兩個交直觀、形象的動態(tài)幾何環(huán)境，通過學生們自己動手操作，得到最終的結果后，同學們都十分興奮，取得了良好的教學效果。

1.4 有利于培養(yǎng)學生創(chuàng)造性思維思維的創(chuàng)造性是指完成思維活動的內(nèi)容、途徑和方法的自主程度，并通過獨立思考創(chuàng)造出有一定新穎的成分，尋求變異，勇于創(chuàng)新。它常以廣泛的聯(lián)想，引申及轉(zhuǎn)換等思維方法為基礎。而有關軌跡的教學是幾何中一個重要知識點，且又是一個難點。難就難在需用運動的觀點來看幾何圖形。過去教師借助于靜態(tài)的圖形或教具，試圖通過生動的講解引導學生進入情景，從而在學生頭腦中產(chǎn)生畫面。但結果只有少數(shù)感性知識豐富的學生才能做到。要達到上述目標并非容易，但《幾何畫板》的動畫功能和軌跡功能，可以直觀地演示出軌跡生成的過程，不僅使分析、過程、結果一目了然，而且還由此發(fā)現(xiàn)許多新的規(guī)律。可以幫助我們達到培養(yǎng)學生創(chuàng)造性思維目的，例如在運用幾何畫板繪制橢圓圖形時，學生往往會由橢圓的繪制方法聯(lián)想到雙曲線、拋物線的繪制方法，同時還可以想象出圓錐曲線的統(tǒng)一圖形繪制方法，通過一個方程(可以是普通方程也可以是極坐標方程)變換出三種不同的圓錐曲線圖象。筆者指導一個學生學習橢圓畫法后，該學生就很快總結出橢圓的6種不同畫法，同時在畫橢圓后又利用“跟蹤點”命令想象出幾個旋轉(zhuǎn)體的畫法，令人贊嘆，達到所謂“師不必賢于弟子”的效果，也增強了學生的自信心以及老師自身的教育成功感。教師也頗有“教無止境”之感，激勵教師不斷進取。

1.5 增強學生學習數(shù)學的興趣因為幾何畫板的即時、快捷作圖功能以及動畫、彩色、變換等功能，也可以和用Flash或Authware制作的動畫圖形結合使用，增強了動感效果。《幾何畫板》還可以用于分形幾何作圖，在高中數(shù)學課程標準的數(shù)學文化中提到幾何分形，運用《幾何畫板》可以作出平面幾何中三角形的n極分形、盒子分形、分形樹等。不僅讓學生接觸到了一個全新的數(shù)學發(fā)展領域，還讓學生了解和體會到遞歸思想和迭代方法的重要性，而且又可以深刻形象地理解數(shù)學思想方法，整個過程中可以培養(yǎng)學生的探索能力和創(chuàng)新思維，體驗到新的研究方法，發(fā)展其辯證思維和提高其審美情趣，增強對數(shù)學的學習興趣。

1.6 有利于提高解題效率《幾何畫板》不僅能夠動態(tài)地展現(xiàn)出幾何對象的位置關系、運行變化規(guī)律，是數(shù)學教師制作課件的有利工具，有較強的作圖功能，還可以借助于《幾何畫板》做出圖象，觀察圖象的動態(tài)變化，進而把“數(shù)”的問題轉(zhuǎn)化為“形”的問題，把抽象的問題轉(zhuǎn)化為直觀的問題，對解函數(shù)類代數(shù)題題有很大的幫助。要想研究函數(shù)性質(zhì)，最直接的方法就是利用函數(shù)的圖象，我們在分析這類問題時，利用《幾何畫板》繪制函數(shù)圖形，提高了學生對圖的重視程度，特別是讓學生學會利用性質(zhì)作圖、利用圖象來分析函數(shù)性質(zhì)，培養(yǎng)了學生的數(shù)形結合思想象來分析函數(shù)性質(zhì)，培養(yǎng)了學生的數(shù)形結合思想。

例1 (2008年四川高考題)已知函數(shù)f(x)=16ln(1+x)+x2－10x，若直線y=b與函數(shù)y=f(x)的圖象有3個交點，求b的取值范圍。

解:

所以f(x)的單調(diào)增區(qū)間是(－1，1)，(3，+∞)，所以f(x)的單調(diào)減區(qū)間是(1，3)。

所以f(x)的極大值是f(1)=16ln2－9，極小值是f(3)=32ln2－21。

因此可得

所以在f(x)的三個單調(diào)區(qū)間(－1，1)，(3，+ ∞)，(1，3)上，直線 y=b與y=f(x)各有一個交點，當且僅當f(3)＜b＜f(1)，b的取值范圍是(ln2－21，16ln2 －9)。

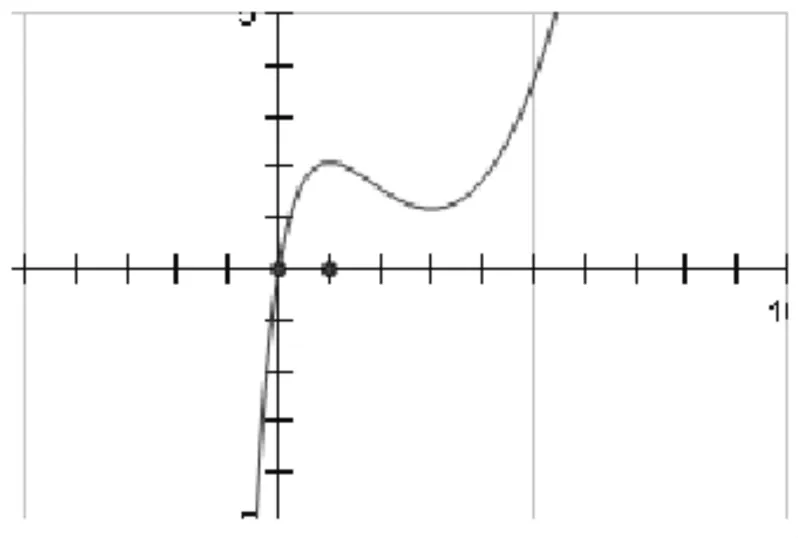
圖1

1.7 和其他信息技術工具相互配合，優(yōu)化授課效果如果數(shù)學老師能夠在中小學數(shù)學教學中把相關的軟件進行有機組合搭配，會達到事半功倍的效果，大大提高數(shù)學課堂教學效率，例如:在解析幾何教學中如果能夠運用MATLAB或Mathmatics軟件用于作圖，可以形象顯示出馬鞍面、玫瑰曲線、心臟形曲線以及其他各種相對復雜而且用《幾何畫板》難以畫出的復雜函數(shù)曲線，用《幾何畫板》繪制的圖形可以輕松復制到幻燈片(PPT)中，也可以用超鏈接方式和幻燈片銜接使用，設計整體性數(shù)學教學課件。

2 高師數(shù)學專業(yè)學生及在職數(shù)學教師對幾何畫板的掌握情況

筆者在擔任數(shù)學課的瓊州學院數(shù)學系2004級、2005級、2006級專科班，2003級、2004級、2005級、2006級本科班400多學生的調(diào)查中得知:對幾何畫板熟練掌握的人幾乎沒有，基本掌握的有4人，基本都是在中學階段看到有老師使用而感興趣自學的，絕大多數(shù)同學對幾何畫板一頭霧水。對海南省參加省級在職初中數(shù)學教師教師培訓班的來自全省各縣22名學員的調(diào)查結果顯示:只有一名教師能夠運用幾何畫板作簡單初中幾何點、線、圓、矩形等基本的圖形，其他命令基本不會使用，其余老師完全不會使用幾何畫板，訪談后了解到，這些學員中有兩個教師在自己工作的學校曾經(jīng)見到有同事使用幾何畫板輔助教學。大多數(shù)學員聽說過這個工具，但是因為沒有學習機會，一直不會使用。

3 高師數(shù)學專業(yè)有開設幾何畫板的必要性

《幾何畫板》在數(shù)學教學中具有傳統(tǒng)教學方法無法比擬的巨大優(yōu)勢，只要數(shù)學教師能在平常的數(shù)學教學中主動、自覺地應用《幾何畫板》為教學服務，就能更好地培養(yǎng)學生自主學習、探究問題的能力，就能激發(fā)和調(diào)動學生進行學科學習的積極性，就能把學生從庸俗的電腦游戲中解脫出來，利用電腦為自己的學習服務。《幾何畫板》作為一個學生自主學習的平臺，必將為學生的自主學習、探究學習提供一個廣闊的空間，成為培養(yǎng)學生創(chuàng)新思想的實踐園地，但是這種優(yōu)勢與在職數(shù)學教師和高師數(shù)學專業(yè)在校大學生對該軟件的掌握情況形成鮮明反差，因此，高師數(shù)學專業(yè)應該將此課程作為必修課程，引導大學生以《幾何畫板》為工具大膽開發(fā)相關數(shù)學課件，開展輔助教學授課比賽等各種活動，極力大學生尤其是即將就業(yè)成為數(shù)學教師的畢業(yè)班學生熟練掌握這個對中小學數(shù)學教師的教學工作非常有幫助的工具。

［1］陶維林.幾何畫板實用范例教程［M］.北京:清華大學出版社，2001:46－65.

［2］傅金泉.利用《幾何畫板》培養(yǎng)學生自主探究學習［J］.網(wǎng)絡科技時代，2007(6):23－25.

［3］潘卓.利用《幾何畫板》制作分形幾何圖形［J］.中學數(shù)學月刊，2008(7):33－35.

［4］周國華.幾何畫板與解題研究［J］.延邊教育學院學報，2009(2):113－116.

［5］徐祖德.用《幾何畫板》探究圖形性質(zhì)的不變性［J］.中學數(shù)學月刊，2009(8)):31－32.