速度脈沖激勵作用下混凝土框架柱抗剪性能研究

周 靖， 方小丹

（華南理工大學 亞熱帶建筑科學國家重點實驗室，廣州 510641）

速度脈沖地震作用導致混凝土柱抗剪性能下降而造成建筑結構剪切脆性破壞和倒塌的現象，近年來引起專家學者的廣泛關注［1－4］。如在2008年汶川地震以及1995年日本阪神地震中，不少建筑物中間樓層或底層框架柱出現抗剪破壞或彎剪破壞而導致結構整體或整層倒塌的情況［5－6］。基于大量震害調查并結合試驗和數值模擬分析，發現水平和豎直速度脈沖聯合地震作用下，混凝土柱容易形成剪切破壞，隨著剪切破壞機制的形成和發展，框架柱豎向承載力損失很快，進而導致結構的整體倒塌或連續倒塌［2］。速度脈沖地震作用下框架柱容易形成剪切破壞機制的主要原因：一方面是水平向速度脈沖地震效應增大了混凝土柱的抗剪需求，另一方面豎向脈沖地震效應則通過高幅值的拉壓作用降低了柱的抗震受剪承載能力，同時伴隨有框架柱強度和剛度的快速退化［1，3］。然而，受制于工程結構豎向和水平向聯合速度脈沖地震動效應研究的復雜性以及抗剪性能研究手段的缺陷，目前關于速度脈沖地震效應對混凝土柱抗剪性能影響的研究很少，國內尚沒有相關的報道。最近，Kunnath［1］研究了混凝土橋墩的抗震性能，結果表明豎向速度脈沖地震作用下橋墩的抗剪承載力有顯著的減小。Zaghlool［7］研究混凝土框架結構在水平和豎向速度脈沖和非速度脈沖地震作用下的抗剪需求和抗剪能力，結果表明速度脈沖地震作用下柱更容易出現脆性破壞；Austin［8］針對雙橋柱結構的研究得到相似的結論。Elnashai［9］的試驗研究表明柱和墻等豎向構件的抗剪性能對豎向激勵十分敏感。

現有的研究多數專注于橋梁結構的橋墩抗剪性能，尚停留在定性的評估，考慮其他因素如框架柱或橋墩的剪跨比、豎向和水平向加速度耦合峰值比、加速度峰值輸入時差以及振動周期等綜合影響的最不利抗剪性能的研究工作極少。相對橋梁結構，一般的建筑結構豎向振動周期短，框架柱在速度脈沖地震作用下的抗剪性能如何，尚有待展開研究。鑒于此，本文以混凝土框架結構為分析對象，通過豎向和水平向等效速度脈沖聯合激勵下的動力時程分析，研究速度脈沖地震效應及其相關因素的影響規律，建立考慮速度脈沖效應對混凝土框架柱抗剪性能影響的定量預測模型，為近斷層速度脈沖地震作用下混凝土柱的抗震設計以及理論和試驗研究提供可借鑒的參考。

1 輸入激勵與結構模型

1.1 輸入激勵

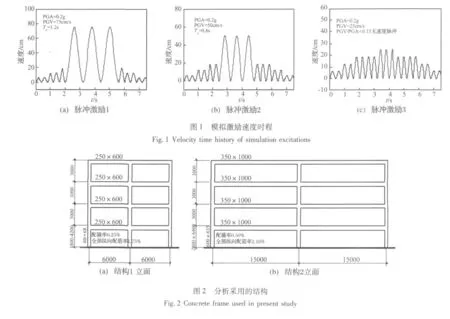
影響速度脈沖地震動強度的因素較多，定量地研究混凝土框架柱的抗剪性能，勢必需要大量的不同速度脈沖強度的地震動記錄進行時程分析，時耗太大。本文采用Makris［10］給出的正弦等效速度脈沖激勵進行研究。圖1列出了3條等效速度脈沖激勵的速度時程，分別代表強速度脈沖、中等速度脈沖和一般速度脈沖記錄。速度脈沖強度以PGV（峰值速度）與PGA（峰值加速度）之比（PGV/PGA）表征。通過變化加速度頻譜特性，衍生另外3條速度脈沖激勵，6條速度脈沖激勵的PGV/PGA變化范圍0.127～0.478。等效速度脈沖激勵的總持時以及加速度峰值PGA相同，而速度脈沖峰值PGV、脈沖周期Tp以及脈沖循環數N不同。速度脈沖參數［11］（PGV和Tp）的標準參考國內外相關研究選定典型數值，斷層距一般在0～25 km。當PGV/PGA≤0.15，速度脈沖效應很小，認為是非脈沖激勵。

1.2 選用的結構

設計兩榀兩跨四層平面混凝土框架結構，以其底層柱為考察對象，立面示意如圖2所示。圓柱體抗壓強度特征值25.3 kN/mm2（對應中國規范的C30），抗拉強度 2.515 kN/mm2，最大應變 0.002；縱向鋼筋HRB335；橫向鋼筋HPB235，屈服強度按規范值設定。

1.3 程序驗證

采用結構彈塑性分析程序 Seismostruct［12］進行動力分析。Seismostruct程序是專業為地震工程研究開發的動力和靜力分析模擬平臺，纖維材料模擬結構構件，目前已廣泛應用于地震工程研究。為驗證程序分析混凝土框架柱抗剪性能的有效性和敏感性，首先對一根彎剪破壞的混凝土柱抗剪擬靜力試驗結果進行模擬分析［13］，以確定程序的相關設置參數。材料本構模型為：鋼筋采用Menegotto-Pinto模型，混凝土采用非線性變約束模型［12］。試驗測試和數值分析的結果比較如圖3所示。二者的最大載荷水平、位移以及剛度和強度退化趨勢都有較高的吻合性，表明本程序能夠開展混凝土框架柱的抗剪性能數值模擬研究。

圖3 試驗結果與分析結果的比較Fig.3 Comparison of analysis data and test data

2 參數分析

2.1 速度脈沖強度的影響

以框架結構1為對象（水平和豎向基本振動周期分別為0.792 s和0.098 s），分析脈沖激勵作用下混凝土柱的抗剪需求和抗剪承載力，其中考慮地震作用組合的框架柱斜截面抗震受剪承載力計算分別按中國混凝土結構設計規范的抗剪強度模型（CS模型，如式（1））和Sezen研究的抗剪強度模型［14］（SS模型，如式（2））。

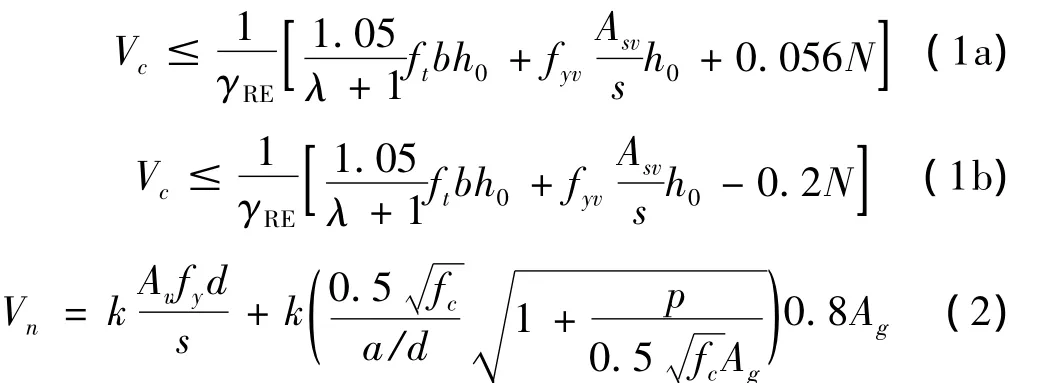
式（1）中符號含義同混凝土設計規范（GB50010—2010）。式（2）中，k為考慮延性水平的修正系數；Av為箍筋面積；fy為箍筋強度；d為極限壓應變點到縱向受拉鋼筋的距離；s為箍筋間距；a/d為剪跨比；fc為混凝土圓柱體抗壓強度；p為軸向荷載；Ag為柱毛截面面積。

水平向PGA調幅到0.5 g，豎向與水平向PGA之比（V/H）設定為2/3，同時水平向加速度與豎向加速度峰值輸入時差0.3 s，得到相對最不利抗剪性能點。圖4和圖5為底層中間框架柱的抗剪需求和相對于初始軸壓力的軸壓時程比較。從圖可知，速度脈沖越大，框架柱的抗剪需求峰值越大，這與其他研究［4］的結論是一致的；而速度脈沖強度越大，框架柱的峰值軸壓力在速度脈沖時間段反而較小，這一趨勢后續做進一步的探究。

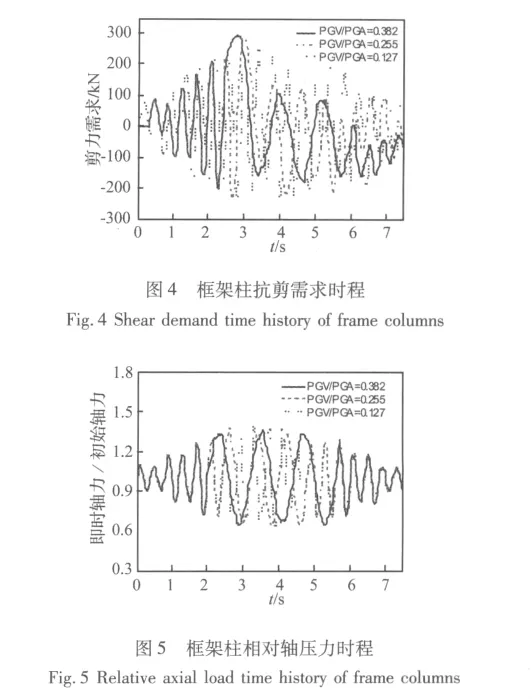
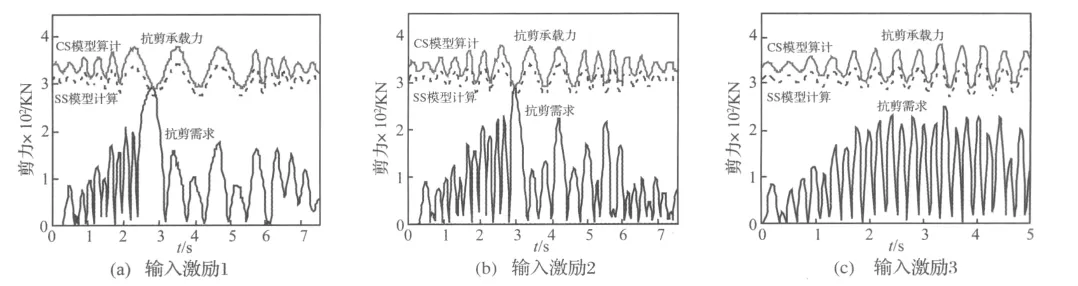
圖6 即時抗剪承載力與抗剪需求比較Fig.6 Instant comparison of shear capacity and shear demand

根據抗剪需求不同時刻對應的即時軸壓力，分別按CS和SS模型計算柱即時抗剪承載力。把反向抗剪需求鏡像在正向一側，繪制即時抗剪承載力與抗剪需求時程如圖6。從圖6可知，在PGA相同的速度脈沖激勵作用下，脈沖速度強度越大，則抗剪性能最不利時刻抗剪需求超越抗剪承載力的可能較大，這表明速度脈沖強度對抗剪性能有重要的影響。另外，CS模型計算的抗剪承載力總體上比SS模型的計算結果偏大。

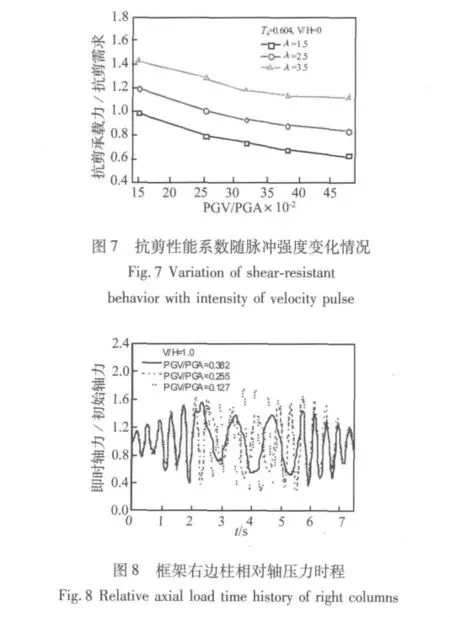
為便于表述，定義框架柱的抗剪承載力與抗剪需求之比為抗剪性能系數ρ。采用不同輸入條件和結構配置進行分析，ρ隨速度脈沖強度變化的趨勢如圖7，隨PGV/PGA增大，ρ減小。一般的，隨柱剪跨比增加，抗剪承載力減小，抗剪需求也減小，但抗剪需求減小的幅度更大，因此剪跨比越大，抗剪性能系數越大。

2.2 加速度峰值比和振動周期的影響

耦合地震作用即豎向和水平向加速度同時施加且同時達到各自的最大值或最小值。強震記錄表明近斷層豎向與水平向加速度峰值比（V/H）遠超過現行設計規范規范規定的2/3，如1994年Northridge地震 V/H高達1.79，1995年神戶地震 V/H 高達1.96，研究表明豎向地震作用的影響主要表現在豎向與水平向加速度峰值比較大的區段［3］。

為了探究耦合峰值比和振動周期對抗剪性能的影響，選用框架結構2（水平和豎向基本振動周期分別為0.809 s和0.253 s）進行分析，同時研究長周期速度脈沖激勵作用下框架柱軸壓力的變化規律。框架柱軸壓力時程分析結果如圖8所示。雖然耦合峰值比和豎向振動周期都有較大增加，但在速度脈沖時間段，軸向壓力增減幅度隨速度脈沖強度增大反而減小。進一步增加樓層數，其變化趨勢基本一致。深入探究其原因發現，對一般的多層中、短跨結構來說，豎向振動周期比速度脈沖周期小，不出現共振現象，非速度脈沖激勵周期小，反而軸壓力影響大。因此，速度脈沖地震作用下多層結構軸壓力的變化幅度與大跨度結構［15］以及橋梁結構［1］的軸壓力變化幅度有較大的差異。

以脈沖激勵3為輸入，通過變化豎向PGA調整V/H。將不同V/H對應的抗剪需求和對應即時抗剪承載力列出，如圖9（a）。從圖可知，峰值比增大，抗剪需求稍有減小，而抗剪承載力因軸壓力的大幅度變化（圖9（b））出現較大的波動，最不利抗剪承載力隨峰值比增大迅速下降，表明豎向地震動對混凝土柱的抗剪性能有較大的影響（圖9（c））。隨峰值比增加，抗剪性能系數基本呈直線減小；隨脈沖強度增加，抗剪性能系數減小，不同脈沖強度水平的下降趨勢有些差異，脈沖強度越大減小趨勢越大，表明峰值比和速度脈沖強度存在一定的交互影響，但并不是很顯著。

設定峰值比為2/3，保持結構水平振動周期不變，增大豎向振動周期。隨豎向振動周期的增大，抗剪需求基本不變，而豎向軸壓力變化幅度隨豎向振動周期增大而增大，但主要是增大受壓側（＞1），反向減小壓力側（＜1）變化不是很大，如圖10（a）所示。如前所述，豎向速度脈沖作用并不會增加軸向拉壓力峰值，因此，相對而言豎向振動周期與速度脈沖的交互作用對柱最不利抗剪性能的影響不大。

豎向振動周期不變，增大水平振動周期。如圖11所示，隨水平振動周期的增大，抗剪需求增大，抗剪性能系數ρ隨水平振動周期增大而減小；水平振動周期越大，ρ的減小趨緩。不同脈沖強度水平ρ的變化趨勢有較大差異，表明水平振動周期與速度脈沖有較大的交互影響。

2.3 加速度峰值輸入時差的影響

已有的研究表明，當強震記錄站臺離震源不超過5 km，豎向和水平向地震動可同時達到；而當震中距超過5 km之后，豎向地震動先于水平向地震動到達記錄站臺的時間差隨震中距不同而異［16］。事實上也并非豎向和水平向地震動耦合，結構的地震響應出現最不利情況。對給定的結構系統，當水平向激勵與豎向激勵加速度峰值輸入出現一定的相位差時，抗剪能力與抗剪需求之比出現最不利情況。

以激勵3為地震輸入，分析相位差0°～120°（對應峰值輸入時差0 s～1.2 s）的抗剪性能系數。采用結構1（水平和豎向基本振動周期分別為0.792 s和0.098 s），設定加速度峰值比為1.0；采用結構2（豎向和水平基本振動周期分別為0.758 s和0.211 s）設定加速度峰值比為1.5。分析結果如圖12，抗剪性能系數隨峰值時差出現先減小，后增加，再減小的變化規律，抗剪性能最不利位置出現在時差0.2 s～0.6 s段，邊柱和中間柱也有些差異。以上變化趨勢表明豎向與水平向激勵加速度輸入時差對框架柱抗剪性能有重要影響。但是，在本文的研究中，隨輸入激勵和結構系統的不同，分析結果總體表現出無序的規律，尚有待進一步深入研究。

2.4 剪跨比和初始軸壓比的影響

剪跨比是混凝土構件抗剪承載力評價的重要指標，影響構件剪切破壞的形態。設定加速度峰值比為2/3，加速度峰值輸入時差0.3 s，以結構1（水平和豎向振動周期分別為0.672 s和0.086 s）為分析對象。速度脈沖強度與剪跨比對抗剪性能的交互影響以有脈沖與無脈沖激勵的抗剪性能系數之比（ρv/ρ）表征，如圖13所示（SS模型），抗剪性能系數比出現先增大，然后減小的趨勢，剪跨比越大減小趨勢越大；當剪跨比為2.5時，出現峰值，表明剪跨比過大或過小，速度脈沖的影響都是不利的。

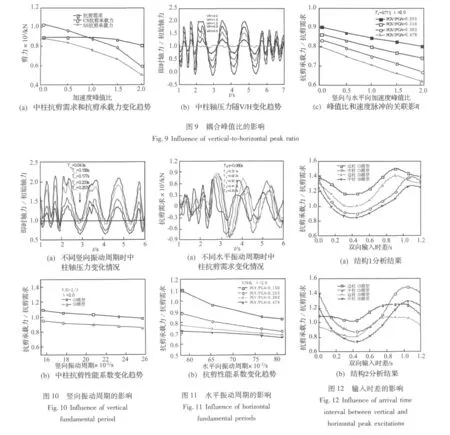
在豎向地震作用下，即時軸壓比回繞初始軸壓比上下波動，因此初始軸壓比制約了軸壓力變化的范圍。設定豎向與水平向加速度峰值比為1.5，PGA時差0.3 s，以結構1（水平和豎向基本振動周期分別為0.459 s和0.061 s）為分析對象，分析速度脈沖強度與初始軸壓比對抗剪性能的影響。如圖14所示（SS模型），隨初始軸壓比增加，抗剪性能系數有增大趨勢；不同速度脈沖強度的ρ曲線保持基本一致的走勢，表明初始軸壓比與脈沖速度對抗剪性能的交互影響較小。

3 綜合分析

綜合前面分析，速度脈沖影響混凝土框架柱最不利抗剪性能的交互因素主要是剪跨比、水平振動周期和峰值比。為了建立考慮速度脈沖及其交互因素影響的最不利抗剪性能定量預測模型，以下針對2種跨度結構、5種脈沖速度強度（0.150～0.478）、5種加速度峰值比（0、0.5、1.0、1.5、2.0）、6 種剪跨比（1.5、2.0、2.5、3.0、3.5、4.0）和 4 種水平振動周期（0.5 s ～ 0.9 s）共1200種工況進行了框架柱最不利抗剪性能系數的計算。加速度峰值輸入時差與采用的結構以及地震動記錄有很大的關系，需通過多次試算才能確定最不利情況，操作性不高，因此本研究中的預測模型，把輸入時差的影響歸并在其他因素中。

在抗剪性能參數分析因素中，有增大抗剪需求者，有減小抗剪承載力者。總體來說，均是外部脈沖荷載效應引起的抗剪性能減小，因此為建立定量預測模型，統一等效為抗剪荷載效應的增加。定義有速度脈沖的ρv與無速度脈沖的ρ之比的倒數為抗剪速度脈沖效應系數ν，ν的物理意義相當于考慮速度脈沖效應影響的剪力作用效應修正系數，ν＞1.0。以PGV/PGA=0.15對應的抗剪性能系數ρ為各相應工況組比較對象。通過對框架中間柱1 200種工況計算結果的整理和分析，可以簡化給出如下定量關系：

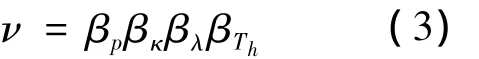
式中：βp=c1p2+c2p+c3，速度脈沖引起的作用效應；βκ=c4κ +c5，豎向與水平向峰值比引起的作用效應；βλ=c6λ2+c7λ +c8，剪跨比引起的作用效應；βTh=c9T2h+c10Th+c11，水平周期引起的作用效應；c1～c11，回歸系數，取值見表1。

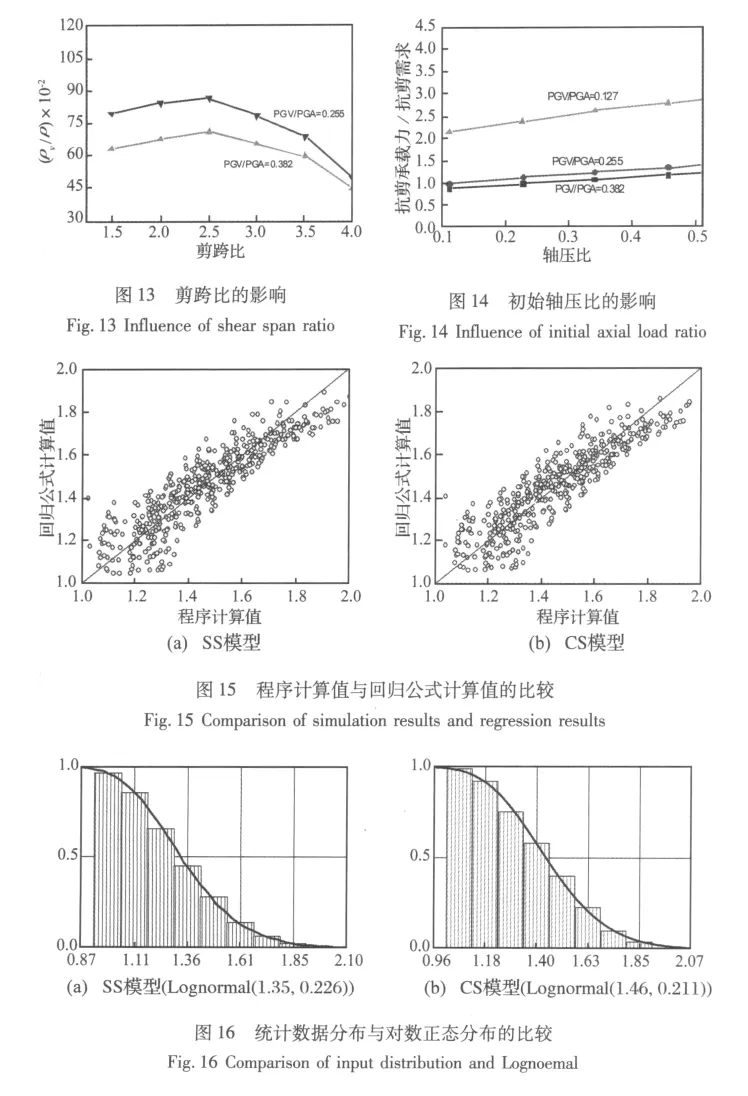
圖15所示為考慮多因素影響抗剪作用效應增大修正系數與回歸公式計算值的對比情況。采用SS模型計算抗剪強度時，二者的相關系數r=0.901，后者與前者之比的平均值為 1.004，標準方差為0.070；采用CS模型計算抗剪強度時二者的相關系數r=0.897，后者與前者之比的平均值為1.006，標準方差為0.068。可見二者有較好的吻合。

鑒于實際的計算時，通過計算公式來估算剪力荷載效應，操作性不強。對于設計計算來說，采用一個滿足一定概率水準的系數來修正，是最簡單實用的方法。通過對前面1 200種計算工況的統計分析，速度脈沖剪力作用效應修正系數符合對數正態分布（K－S檢驗）。基于概率統計模型建立安全概率模型如圖16所示，通過圖中趨勢，可以很好的確定需要的系數水平。以SS模型計算為例，圖中曲線可近似分三個發展趨勢敏感段：左上段（0.87 ～1.11）、右下段（1.61 ～1.85）和中間段（1.11～1.61）。左上段和右下段變化趨勢相對較小，說明此類情況少；中間段下降坡度較大，表明類似情況最多；中間段與右下段的交接點是最敏感點（ν=1.60左右），表明是最不利效應控制有效位置，因此對斷層距在0 km～25 km范圍內的框架柱抗剪設計來說，考慮相應的剪力放大效應是有效的安全保證措施。

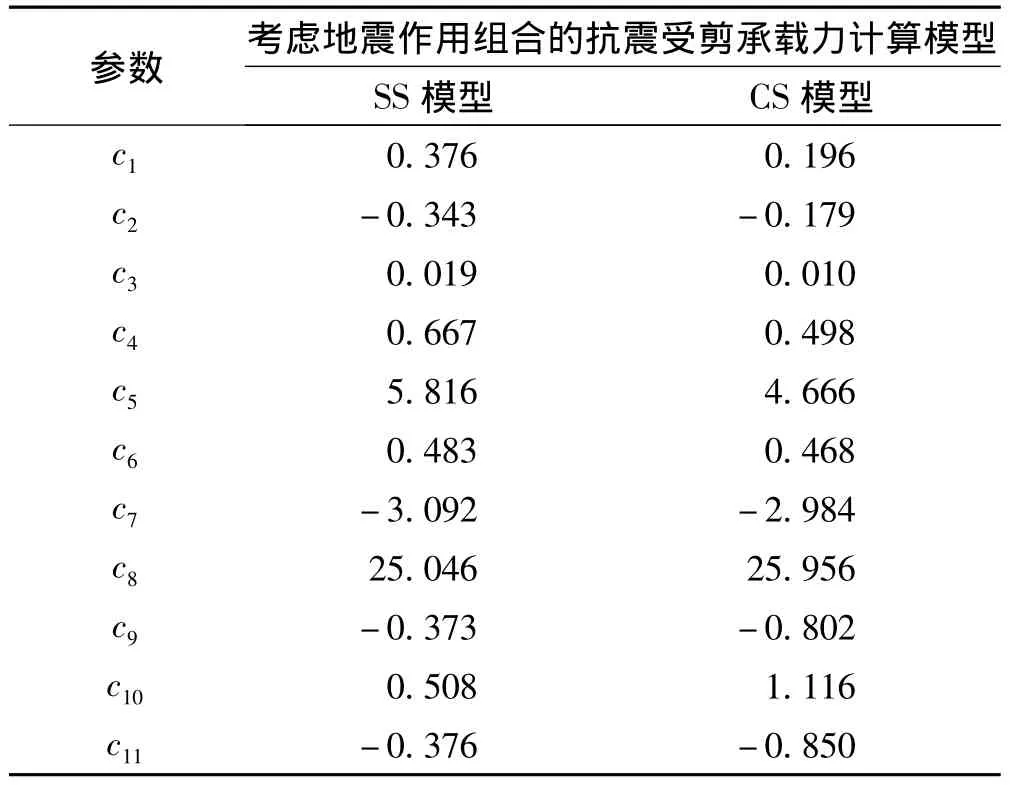
表1 參數c1～c11的值Tab.1 Values of parameters c1～ c11

4 結論

本文分析了速度脈沖強度及其潛在交互因素，如豎向和水平向耦合峰值比、激勵峰值輸入時差、剪跨比、基本振動周期以及初始軸壓比，對框架柱抗剪性能的影響規律。通過對大量計算結果的分析整理，建立了框架柱考慮速度脈沖效應及其交互因素影響的剪力作用效應修正系數預測模型。通過本文研究，可得到如下初步結論：

（1）速度脈沖強度對框架柱的抗剪性能影響很大，隨速度脈沖強度增加，框架柱抗剪需求增大，抗剪性能降低。近斷層地震區域的抗剪設計應考慮速度脈沖效應的影響。

（2）隨著豎向和水平向加速度峰值比的增大，框架柱的最不利抗剪性能呈直線降低。

（3）豎向和水平向加速度峰值輸入時差對框架柱的最不利抗剪性能有顯著影響，影響規律較為復雜。

（4）水平振動周期對最不利抗剪性能有重要影響，水平振動周期增大，抗剪性能降低。水平振動周期與速度脈沖有一定的交互影響

（5）剪跨比與速度脈沖強度有重要的交互影響，剪跨比增大，抗剪性能總體提高；但速度脈沖強度越大，抗剪性能提高比率相對較小。

（6）對中短跨多層結構，豎向振動周期和初始軸壓比與速度脈沖對框架柱抗剪性能的交互影響小。

［1］Kunnath S，Erduran E，Chai Y H，et al.Effect of near-fault vertical ground motions on seismic response of highway overcrossings［J］.Journal of Bridge Engineering，2008，13（3）：282－290.

［2］ Elwood K J，Moehle J P.Dynamic shear and axial-load failure of reinforced concrete columns［J］.Journal of Structural Engineering，2008，134（7）：1189 －1198.

［3］ Zhang J，Elnashai A.Investigation of RC columns under multi-directional motions［A］.Proceedings of the US-Japan Workshop on Large-scale Experimentson the Seismic Performance of Bridges，San Francisco，USA，2005.

［4］Orozco G L，Ashford S A.Effects of large velocity pulses on reinforced concrete bridge columns［R］.Pacific Earthquake Engineering Research Center，College of Engineering University of California，Berkeley.PEER Report 23，2002.

［5］Hiroshi A.Collapse modes of structures under strong motions of earthquake［J］.Annals of geophysics.2002，45（6）：791 －798.

［6］霍林生，李宏男，肖詩云，等.汶川地震鋼筋混凝土框架結構震害調查與啟示［J］.大連理工大學學報，2009，49（5）：718－723.

［7］Zaghlool B S. Behaviourofthree-dimensionalconcrete structures under concurrent orthogonal seismic excitations［D］.University of Canterbury，New Zealand，2007.

［8］Brown A，Saiidi M S.Investigation of near-fault vs.far field ground motion effects on a substandard bridge bent［A］.24thUS-Japan Bridge Engineering Workshop，Minneapolis，2008.

［9］Elnashai A，Spencer B，Kuchma D.Analysis and distributed hybrid simulation of shear-sensitive RC bridges subjected to horizontal and vertical earthquake ground motion［A］.37thUS-Japan WorkshoponWindandEarthquake， Osaka，Japan，2005：16－21.

［10］ Makris N，Roussos Y.Rocking response and overturning of equipment under horizontal pulse-type motion［R］.Pacific Earthquake Engineering Research Center，College of Engineering University of California，Berkeley.PEER Report 05，1998.

［11］ Rodriguez M A，Bray J D，Abrahamson N A.An empirical geotechnical seismic site response procedure［J］.Earthquake Spectra，2001，17（1）：65－87.

［12］ Seismo Struct-A computer program for finite element analysis［EB/OL］.Available from URL：http：//www.seismosoft.com，2010－08－15.

［13］ Ono A，Shirai N，Adachi H.Elasto-Plastic behavior of reinforced concrete column with fluctuating axial force［J］.Transactions of the Japan Concrete Institute，1989，11：239－246.

［14］ Sezen H，Moehle J P.Shear strength model for lightly reinforced concretecolumns［J］. JournalofStructural Engineering，2004，130（11）：1692－1703.

［15］周 靖，周 飛，蔡 健，等.脈沖型豎向地震作用下大跨度RC帶腋撐框架結構彈塑性動力響應分析［J］.工程力學，2010，27（6）：113－119.

［16］ Collier C J，Elnashai A S.A procedure for combining vertical and horizontalseismic action effects［J］. Journalof Earthquake Engineering，2001，5（4）：521－539.