拋光機磨頭結構改進及其對振動的影響實驗研究

邵俊鵬，徐 斌

(哈爾濱理工大學 機械動力工程學院，哈爾濱 150080)

陶瓷拋光磚是現代建筑裝修工程中應用最為廣泛的陶瓷制品之一，目前國外的陶瓷拋光磚加工技術比較成熟，Orts［1-10］等在陶瓷墻地磚的拋光質量的研究方面做了大量的工作。目前應用最為廣泛的是擺動式瓷磚拋光機，其磨頭工作原理［11］如圖1所示。其原理為電機1通過帶輪2、4帶動主軸旋轉，而后通過剛性連接帶動主動齒輪3，帶動從動齒輪6、凸輪5旋轉。磨盤在公轉的同時，通過差動輪系，使凸輪5相對磨盤產生一個相對運動，凸輪驅動主動擺桿7，主動擺桿又驅動從動擺桿11。使連接在擺桿上的磨塊座8、12做往復的擺動。擺動式拋光機在拋光過程中也會出現表面粗糙度不均勻，瓷磚震碎、瓷磚甭角等情況。針對這些問題，湯迎紅［12］等優化了拋光盤的凸輪曲線，解決了柔性沖擊問題。吳南星［13］等用加水方法控制噪聲。

近年來磨頭振動導致瓷磚碎裂一直是企業的老大難問題。拋光機在拋光瓷磚的過程中，經常出現磨頭振動異常劇烈的情況，操作人將磨頭上的磨塊去掉一個后，磨頭振動便減小了。

受此現象的啟發，本課題對擺動式拋光磨頭進行改進，分析改進后的磨頭對振動的影響，并進行試驗。結果證明，改進后的磨頭有很好的減振作用。

圖1 擺動拋光磨頭原理示意圖Fig.1 Schematic diagram in kind of the swing-style tile lapping grinding head

1 改進后磨頭結構及運行分析

1.1 改進后磨頭結構

圖2為改進后的磨頭結構圖。圖中6是一個和磨塊座形狀相同的配重塊。在運行過程中，這個配重塊和其他磨塊座一樣，做擺動。其高度和磨塊座的高度一樣。1、2、3、4、5是裝有磨塊的磨塊座。5個磨塊座和1個配重塊均勻分布在磨頭的圓周上。磨頭改進前6號位置是一個與5一樣的磨塊座。

圖2 磨頭改進結構Fig.2 Schematic diagram of improved structure of grinding head

1.2 改進后磨頭運行分析

根據擺動式磨頭的原理可知，磨塊座和磨塊在運行中，繞著主軸旋轉還繞著自身軸線擺動。從圖3中可知，磨塊是成對擺動，相互平衡的。凸輪波形一側面驅動時，配重塊6和磨塊座5相對擺動相互平衡。凸輪波形另一測面驅動時，配重塊6和磨塊座1相對擺動相互平衡。由于配重塊6的重量和磨塊座的重量相等。配重塊6只能平衡掉磨塊座5自身重量產生的力，磨塊的重量產生的力無法平衡掉。磨塊座5在運行時，產生單獨的擺動力。同理磨塊座1也是單獨擺動。

圖3 磨頭運行Fig.3 Schematic diagram of the workings of grinding head

2 改進后磨頭激振力方程建立

2.1 磨頭坐標系建立

因磨頭工作時是水平放置在工作臺上的。如圖4所示。取磨頭磨塊底面所在平面的中心為坐標原點O;磨頭的軸線方向為Z軸，Z軸與瓷磚面是垂直的;磨頭擺動方向為Y軸;水平方向為X軸。磨頭角速度方向的正向按照右手定則與Z軸正向一致。

圖4 磨頭坐標系Fig.4 Coordinate system of grinding head

圖5 磨頭激振力Fig.5 Exciting force of grinding head

圖6 磨塊激振力與激振力矩Fig.6 Exciting force and moment of grinding block

2.2 磨頭運行時產生的激振力

通過改進后磨頭的結構和運行分析得知，磨頭磨塊3和配重塊6不對稱誤差造成磨頭的不平衡激振力。磨頭上各個磨塊的軸向反力除了大小有變化外，其合力的中心并不通過磨頭旋轉軸的中心線，因此對磨頭軸中心產生一個軸向反力Fz和一個彎矩。這個彎矩可以分解為y、x方向的力矩Mx、My。如圖5所示。同理，磨頭各個磨塊的旋轉阻力的合力不等于零，形成了側向分力。這個合力可以分解為y、x方向的分力Fy、Fx。

因此，磨頭在運行時，所受到的力和力矩有:Fx、Fy、Fz、Mx、Mz、My。如圖 5 所示。

2.3 磨頭激振力方程建立

圖6為磨頭激振力和激振力矩模型，圖中表示磨頭中第i個磨塊在轉角θi位置，取半徑為r與r+dr間寬度為dr的磨塊體。

軸向反力dFzi和切向阻力dPi為:

式中，Fz(r，θi)dr和Pi(r，θi)dr分別在半徑r處、轉角為θi時單位寬度磨塊體所受的軸向反力和切向阻力。

軸向反力dFzi作用在離磨頭中心為r的位置上，對磨頭產生的力矩為r·dFzi，該力矩可以分解為繞著x軸的彎矩dMxi和繞著y軸的彎矩dMyi為:

切向阻力對磨頭產生一個反扭矩dMzi，同時對磨頭有一個側向力作用，這個力可以在x、y軸方向分解為dFxi、dFyi。因此切向阻力產生總的分量為:

將式(1)、式(2)、式(3)得到的3個激振力和3個激振力矩對半徑r進行積分得磨頭激振力方程為:

式中，r0為磨塊底端距離磨頭中心處的距離，如圖6所示;R為磨塊邊緣距離磨頭中心處距離，如圖6所示;z為磨塊數。

周期性變化的軸向反力會引起磨頭垂直方向振動，即Z方向的振動。轉矩會引起磨頭的扭轉振動。切向阻力和彎矩引起磨頭的橫向振動，由于軸向反力遠遠大于切向阻力［14，15］，因此切向阻力和彎矩引起的橫向振動可以忽略。

改進后磨頭的主要振動為垂直方向振動和轉矩引起的扭轉振動。

3 改進后磨頭減振機理

3.1 磨塊擺動對扭轉振動進行減振

通過改進后磨頭的運行分析可知，磨頭運行時，會產生單獨的磨塊擺動運行，無法平衡。其擺動極限如圖7所示。

圖7 磨塊1擺動極限Fig.7 Schematic diagram of wigwag limit of grinding block1

將圖7磨塊1擺動系統簡化為，一個在圓盤(磨頭主體)上距傳動軸線為r(磨塊靠近軸線的那個面距中心的距離)，擺長為L(磨塊長度)，質量為m(磨塊質量)的一個單擺，其懸掛點為A。如圖8所示。

圖8 磨塊1擺動簡化模型Fig.8 Schematic diagram of simplified model of grinding block1

磨頭等效圓盤以等速Ω做回轉運動，設來自等效圓盤上輕微的扭轉干擾力矩T=Msinωt，引起等效圓盤角速度Ω的輕微波動θ2。

該等效系統的運動學方程［16，17］為:

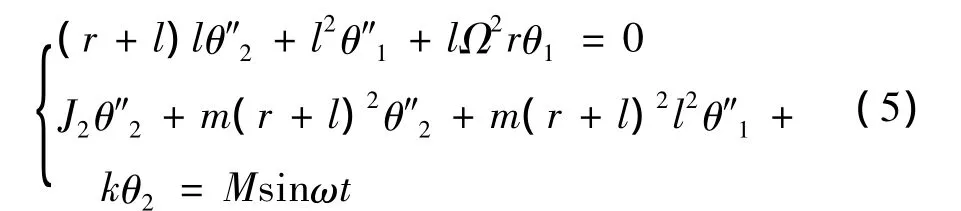
式中，r為磨塊靠近軸線一側到磨頭軸線的距離;L為磨塊長度;Ω為磨頭等效系統轉動角速度;m為磨塊的等效質量;M為干擾力矩的幅值;J2為磨頭的等效轉動慣量;θ2為等效圓盤的扭轉角;θ1為磨塊等效擺的角速度，k為磨頭系統的等效剛度。

方程組(5)的解為:

將式(6)代入式(5)得出確定振幅的矩陣方程:

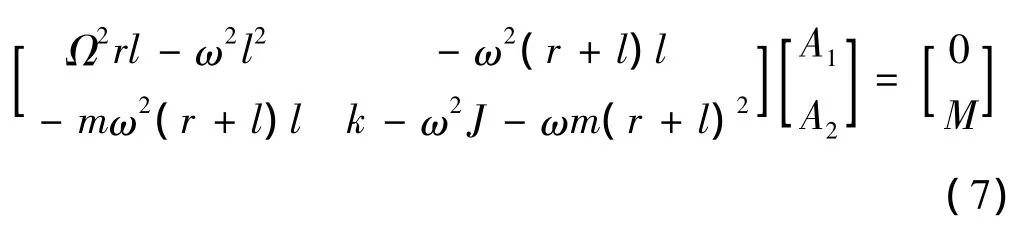
解矩陣得振幅:

設:ω2/Ω2=r/l，得出等效系統的振幅為:

已知(5)式中的:

設 θ2=0，代入式(10)得:

由式(11)得出:

由式(9)，式(12)所表達的關系得出:

當等效擺的固有頻率f等于干擾力的頻率ω時，磨頭等效圓盤的振幅A2=0。擺動磨塊的慣性反力矩正好與磨頭的扭轉干擾力矩平衡，達到減振的效果。

3.2 垂直方向振動的減振

圖9為磨頭垂直振動簡化模型，磨塊座和磨塊合體簡化成為刀體，磨頭簡化為刀座。

圖9 磨頭垂直振動簡化模型Fig.9 Schematic diagram of simplified model of vertical vibration of grinding head

磨塊一點0的動態切削力T分解為垂直切削力Fz和切削阻力P。Fz遠遠大于P。由于磨頭存在著垂直方向的振動Z(t)而引起動態磨削力的變化［18，19］，其變化值為:

式中，Ω為磨頭的角速度;T為磨頭每轉時間;k1為磨削厚度系數;μ為重疊系數，μ≤1.0;z1為同時工作的磨塊數;z2為磨塊總數，z1=z2;K為切入系數;Z(t)為磨頭垂直方向的擾動;Z為垂直方向。

表1 磨頭振動加速度實驗參數Tab.1 Vibration acceleration experimental parameter of grinding head

從式(13)中可以看出，動態磨削力的變化和磨塊數成正比關系。改進后的磨頭磨塊數減少，垂直方向的動態磨削力減小，磨削力平穩。達到了垂直方向振動減小的目的。

4 改進后磨頭振動試驗

為了驗證改進后磨頭的減振機理，按照表1參數進行了磨削振動試驗并按照表1的參數與改進前的磨頭進行了對比。對其減振性進行了檢驗。機床為SD-281型12磨頭的瓷磚拋光機。

實驗時按照表1的參數，利用壓電式傳感器測量X、Y、Z三個方向的振動加速度。所用儀器和測試系統簡圖如圖10所示。按照表的條件進行拋光瓷磚，取磨頭上所得的振動加速度信號，相鄰12個峰值的平均值。其結果如表2所示。改進前后磨頭振動加速度幅值如圖11、圖12所示。

圖12 改進后磨頭振動加速度實測幅值圖Fig.12 Schematic diagram of vibration acceleration amplitude of after improvement grinding head

從圖11、圖12可以看出，改進后的磨頭振動幅值明顯小很多。激振能量分散在各個頻率上。而改進前的激振能量集中在幾個頻率上。同時驗證了改進后磨頭的減振機理的理論分析得出的結論。

通過對比表2中的改進前和改進后磨頭振動加速度值，改進后磨頭的振動加速度顯著減小。在X方向振動加速度值小的只是改進前的50%。

表2 磨頭振動加速值對比表Tab.2 Numerical contrast of vibration acceleration of grinding head

5 結論

通過理論分析和實驗得出:改進后的磨頭減振明顯。同時也驗證了一線工人在磨頭振動很大的時候，拿掉一個磨頭振動減小的事實。也證明了利用改進后的磨頭減小振動的可行性。

［1］ Orts M J S’anchez E，Gareia-Ten J，et al.Porcelain tile behavior during polishing［J］. Bol. delasoe. EsP.de Ceramieay Vidrio，2001，40:447-455.

［2］ Hutchings I M，Xu Y，Sanchez’E，et al.Porcelain tile microstructure:implications for polishability［J］.Journal of the European Ceramie Society，2006，26:1035-1042.

［3］Hutchings I M，Adachi K，Xu Y.Analysis and laboratory simulation of an industrial polishing proeess for porcelain ceramic tiles［J］.Journal of the European Ceramic Society，2005，25:3151-3156.

［4］ Sanchez E，Ibanez M J，Garcia Ten J，et al.Porcelain tile microstructure:implications for polished tile propertyes［J］.Joumalofthe European Ceramic Society，2006，26:2533-2540.

［5］ Fabio J P，Jan Sousa，Aurich C，et al.Kine-matics of a single abrasive particle during the industrial polishing process of porcelain stoneware tiles［J］.Journal of the European Ceramic Society，2007，27:3183-3190.

［6］ Xu X P，Huang H，Gao Y，et al.Processes for the generation of glossiness on ground granites and ceramies［J］.Key Eng.Mater，2003，238(2):99-104.

［7］ Wang C Y，Kang T C，Qin Z，et al.How abrasive machining affects surface Charaeteristics of vitreous ceramic tile［J］ .American Ceramic Soeiety Bulletin，2003，82(10):9201-9208.

［8］ Tucci A，Esposito L，Malmusi L，et al.Wear resistance and stain resistance of porcelain stoneware tiles［J］.Key Engineer Mater，2002，206(2):1759-1762.

［9］Hutchings M，Adachi K，Xu Y.Analysis and laboratory simulation of an industrial polishing process for porcelain ceramic tiles［J］.Journal of the European Ceramic Society，2005，25:3151-3156.

［10］ Braganca S R，Bergmann C P. A view of whitewares mechanicalstrength and microstructure［J］. Ceramics Intemational，2003，29:801-806.

［11］鄧小明，隋旭東，陳仲正，等.新型拋光磨頭擺桿裝置［S］.中國:ZL200920051304.5.2009:12，16.

［12］湯迎紅，吳運新，周 鵬.陶瓷拋光機拋光盤凸輪的改進設計［J］.機械設計，2006，(3):58-60.

［13］吳南星，朱金貴，肖任賢.陶瓷用拋光機磨頭聲-結構分析及噪聲控制［J］.陶瓷學報，2009，30(1):101-105.

［14］任敬心，康仁科，史興寬.難加工材料的磨削［M］.北京:國防工業出版社，1999:19-20.

［15］陳之炎.船舶推進軸系振動［M］.上海:上海交通出版社，1987:48-53.

［16］林 鶴.機械振動理論及應用［M］.北京:冶金工業出版社，1990:77-82.

［17］何渝聲，魏克嚴，洪宗林，等.汽車振動學［M］.北京:人民交通出版社，1990:174-177.

［18］楊 橚，唐恒齡，廖伯瑜.機床動力學［M］.北京:機械工業出版社，1983:199-205.

［19］徐耀信.機床振動學［M］.江西:江西高校出版社，1991:251-260.