正交面齒輪傳動系統分岔特性

楊 振，王三民，范葉森，劉海霞

(西北工業大學機電學院，710072西安，yang95478@163.com)

進入21世紀以來，國外學者［1-4］對面齒輪的嚙合原理、齒輪彎曲強度、齒面接觸強度、切齒及磨齒加工、面齒輪疲勞壽命實驗等進行了研究.國內學者［5-7］近幾年對面齒輪的研究目前主要集中于齒面設計、齒輪彎曲強度、齒面接觸強度、切齒加工等方面，關于其振動特性的研究還處于初期階段.由于面齒輪傳動系統含有間隙、時變嚙合剛度、齒輪誤差等參數，其本質上是一個強非線性系統，其振動特性會直接影響到傳動系統的穩定性和可靠性［8］.

本文建立了包含齒側間隙、時變嚙合剛度、綜合誤差、支承等參數在內的正交面齒輪傳動系統的彎-扭耦合非線性動力學模型，并用PNF方法求解了系統的動力學方程組，經分析后得到了系統分岔特性的變化規律.

1 系統的非線性動力學模型與方程

圖1所示為根據集中參數理論建立的彈性支承下正交面齒輪傳動的系統動力學模型，模型中不考慮繞各坐標軸的擺振.

該模型以直齒輪軸線為x軸，以面齒輪軸線為y軸，并以兩軸的交點作為原點建立全局坐標系Σ:(O x y z).由于小齒輪為直齒圓柱齒輪，齒輪上無軸向作用力，因此只考慮2個坐標方向的支承剛度和阻尼，分別為kij、cij(i=y，z;j=p，g).

設主動輪p有驅動力矩Tp，從動輪g有不變的阻抗力矩Tg.整個傳動系統共有6個自由度，分別為{Yp，Zp，θp，Yg，Zg，θg}T.

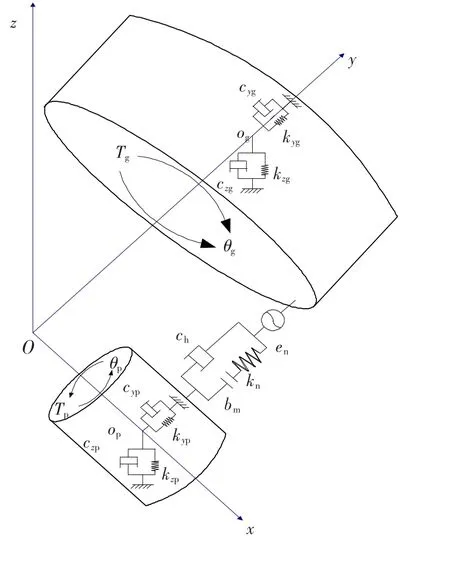
圖1 正交面齒輪傳動系統非線性動力學模型

2 系統的振動微分方程

由圖1可以得到，兩齒輪嚙合點間因振動和誤差產生的沿嚙合點法線方向的相對位移λn為

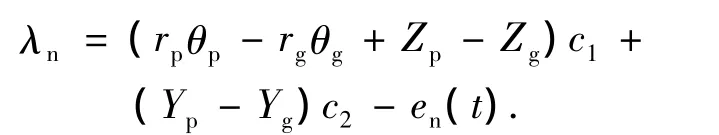
式中:c1=cos αn，c2=sin αn;rp，rg為兩齒輪嚙合點半徑;αn為法面壓力角;en(t)為齒輪副的法向綜合傳動誤差.

則齒輪副在嚙合時的法向動載荷及其沿坐標軸的分力分別為

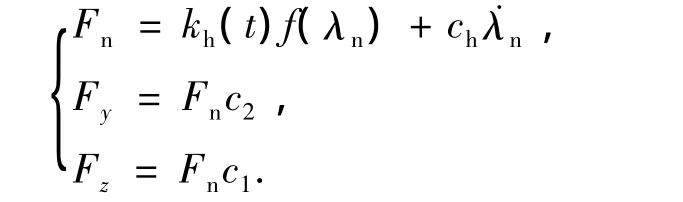
式中:kh(t)為時變嚙合剛度;ch為嚙合阻尼; f(λn)為間隙函數，其中:

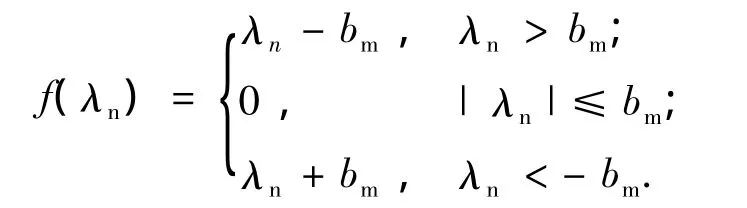
式中，bm為法向平均嚙合間隙之半.

下面確定時變嚙合剛度kh(t)和齒輪副綜合誤差en(t)的表達式.

由于面齒輪的空載重合度一般在1.6～1.8，因此實際的面齒輪副的綜合嚙合剛度是一個以嚙合周期為周期的階躍函數.另外，面齒輪的重合度在加載后會進一步增大，其嚙合剛度的變化比較小，因此可以將其處理為在一個平均值下的微小波動，具體表達式如下:

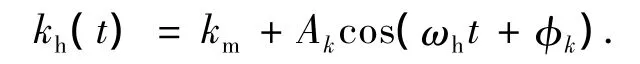
式中，km為嚙合剛度的平均值，Ak為嚙合剛度的波動幅值，ωh為齒輪副的嚙合頻率，φk為初相位.

由于對齒輪振動影響較大的誤差比較多，如基節偏差、齒距偏差、齒形誤差、齒距累積誤差等，在此將其統稱為齒輪副綜合誤差.具體的處理方法參考文獻［9］，將其表示為嚙合頻率的簡諧函數:

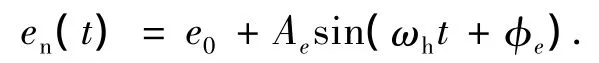
式中，e0為綜合誤差常值，Ae為綜合誤差的幅值，φe為初相位.

則圖1所示的面齒輪傳動系統的振動方程為

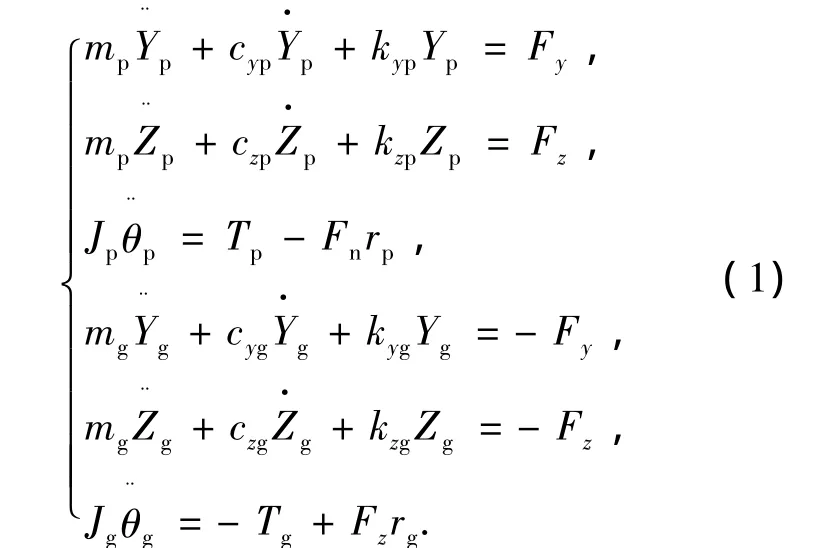
為了消除系統的剛體位移，引入齒面嚙合點間的法向相對位移λn作為新的自由度，并對方程組(1)進行量綱一化處理后，得

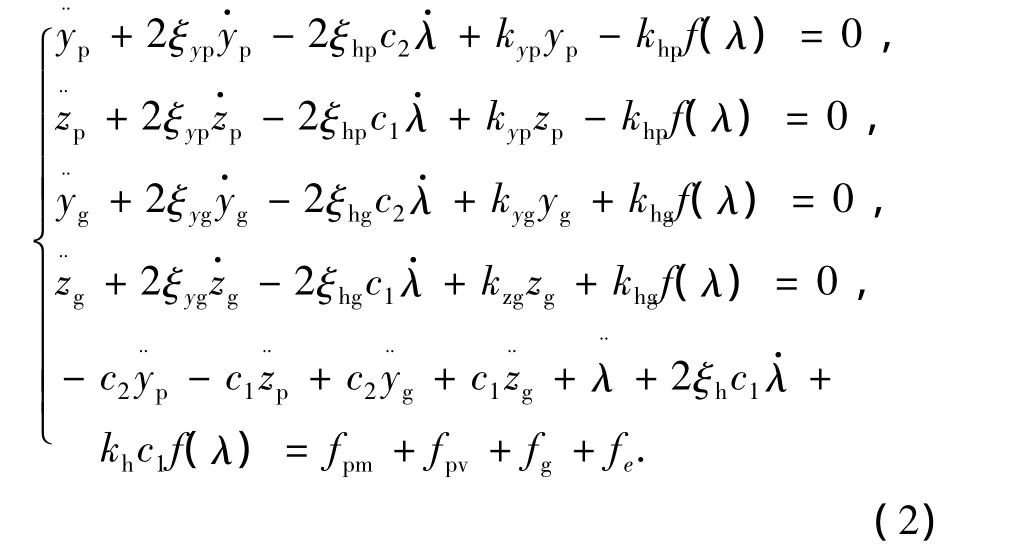
式中:yj=Yj/bm，zj=Zj/bm;λ=λn/bm;

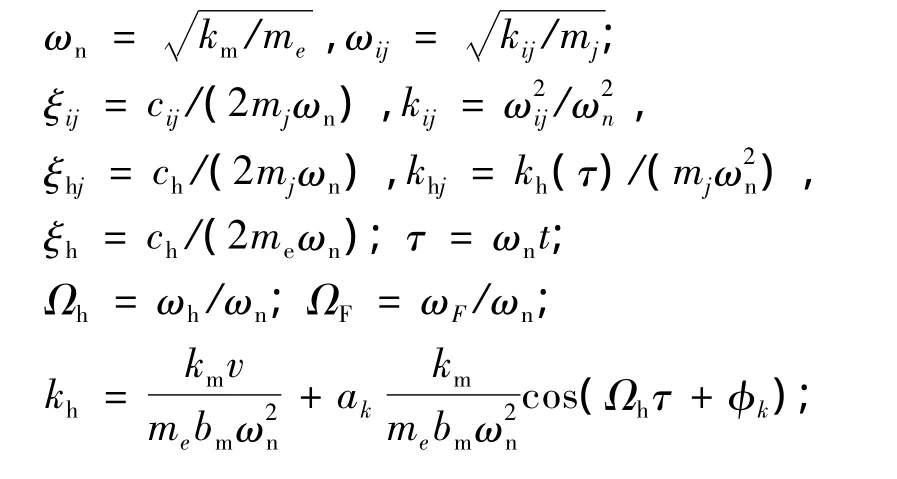
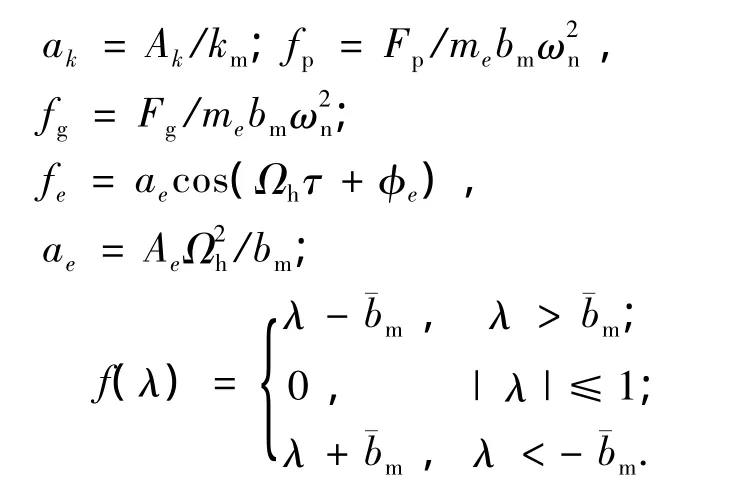
其中，i=y，z;j=p，g.

3 系統的分岔特性分析

對間隙型非線性方程組(2)，用PNF方法(參考文獻［10］)對其進行求解，得到的系統響應也以量綱一化的形式給出.

系統主要參數為:齒數zp=36，zg=123;模數m=4 mm;齒寬B=30 mm;壓力角αn=20°;傳動誤差均值e0=0 μm，幅值Ae=15 μm，初始相位角φe=0;驅動轉矩Tp=300 N·m;負載轉矩Tg=1 025 N·m;齒側間隙bm=100 μm;嚙合剛度km=3.2×108N·m-1;小直齒輪支承剛度kyp=kzp=2.8×108N·m-1，面齒輪支承剛度kyg=kzg=5.2×108N·m-1.

3.1 系統的倍周期分岔

圖2為時變嚙合剛度幅值系數ak從0.4增大到0.5的過程中系統的倍周期分岔特性圖.由系統的龐加萊截面圖可見，在ak=0.420處系統響應依然為5周期次諧響應(圖3(a));當增大到0.460時，系統分岔為 10周期次諧響應(圖3(b));然后在ak=0.485處進一步分岔為26周期次諧響應(圖3(c));其后的分岔域越來越短，最后進入混沌響應(如圖3(d)).

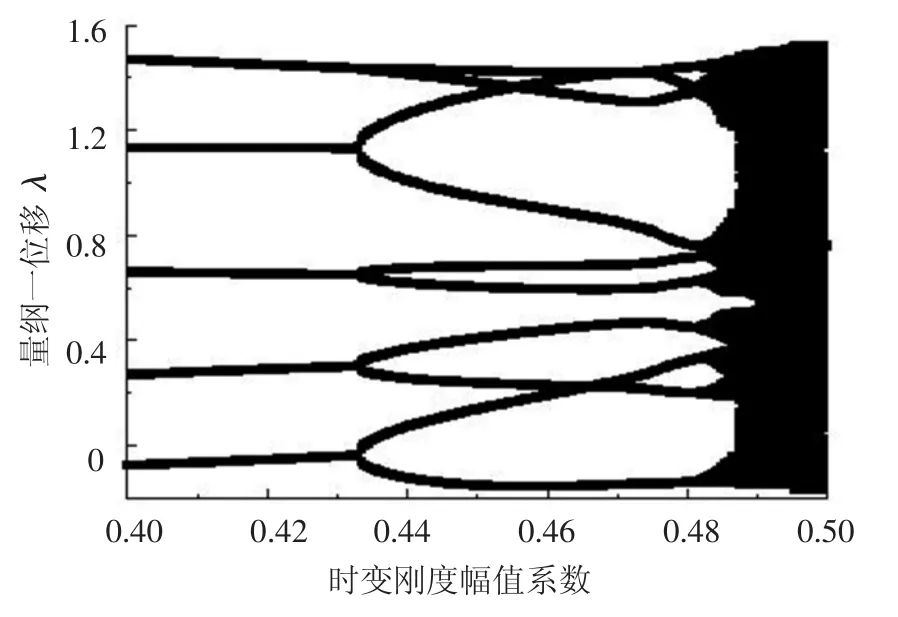
圖2 系統倍周期分岔圖(ak=0.4～0.5)

3.2 系統的擬周期分岔

當嚙合阻尼比ξg由0.061減小到0.060時，可以觀察到系統響應由擬周期道路到達混沌的過程，如圖4所示.

圖3 不同時變嚙合剛度幅值系數ak對應的系統龐加萊截面圖

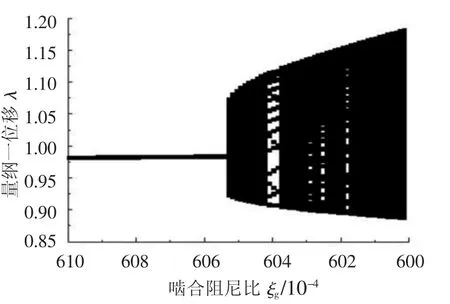
圖4 系統擬周期分岔圖(ξg=0.061～0.060)

由各參數點處系統響應的龐加萊截面圖可見，在ξg=0.060 510 0附近系統響應為擬周期響應，如圖5(a)所示;當ξg減小到0.060 416 9時，系統的擬周期環面破碎為數個小的吸引子區域，如圖5(b)所示;當ξg繼續減小到0.060 390 0時，系統響應為17周期次諧響應，如圖5(c)所示;隨著ξg進一步減小到0.060 375 0附近時，系統再次進入擬周期響應，如圖5(d)所示.經過一系列的擬周期分岔后，系統最終進入混沌響應，此時系統響應相圖和龐加萊截面圖如圖5(e)、圖5 (f)所示.

由以上分析可以看出，嚙合阻尼比從0.061減小到0.060的過程中，系統響應經歷了周期—擬周期—擬周期環破碎—周期—擬周期…的擬周期分岔道路.

3.3 系統的邊界激變

在一定的參數條件下，還可以觀察到系統通過邊界激變到達混沌響應的現象.

圖6所示即為改變綜合傳動誤差幅值ae時系統的激變，當ae=0.116時，系統響應為2周期響應(圖7(a));當ae傳減小到0.115附近時，系統響應發生激變進入混沌響應，如圖7(b)所示.

圖5 不同嚙合阻尼比ξg對應的系統龐加萊截面圖

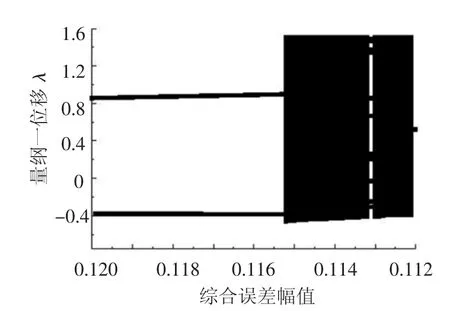
圖6 系統激變分岔圖(ae=0.120～0.112)

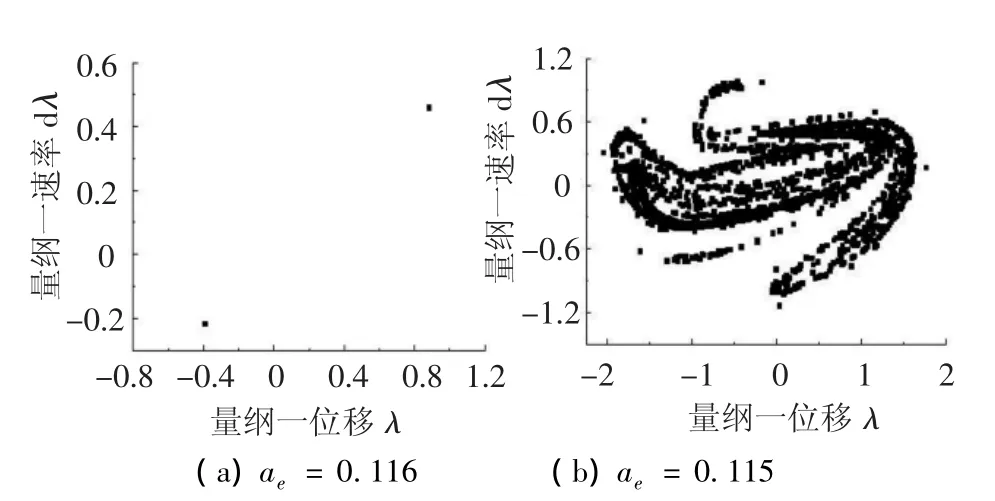
圖7 不同綜合誤差幅值ae對應的系統龐加萊截面圖

4 結論

1)建立了包含支承、齒側間隙、時變嚙合剛度、綜合傳動誤差、阻尼和外激勵等參數的面齒輪傳動系統的非線性動力學模型.

2)系統通向混沌的途徑主要有周期倍化道路、擬周期道路以及邊界激變.

3)不同的系統參數，甚至同一參數的不同區段，系統會以不同的道路進入混沌區域.

［1］LITIVIN F L，ALFONSO F，LAUDIO Z Z，et al.Design，generation and TCA of new type of asymmetric face-gear drive with modified geometry［J］.Computer Methods in Applied Mechanics and Engineering，2001，190(3):5837-5865.

［2］LITIVIN F L，ALFONSO F，CLAUDIO Z Z，et al.Design，generation，and stress analysis of two versions of geometry of face-gear drives［J］.Mechanism and Machine Theory，2002，37(4):1179-1211.

［3］LITIVIN F L，IGNACIO G P，ALFONSO F，et al.Design，generation and stress analysis of face-gear drive with helical pinion［J］.Computer Methods in Applied Mechanics and Engineering，2005，194(9):3870-3901.

［4］GUINGAND M L，de VAUJANY J P，LCARD Y.Analysis and optimization of the loaded meshing of face gears［J］.Journal of Mechanical Design，2005，127(1): 135-143.

［5］李政民卿，朱如鵬.面齒輪插齒加工中過程包絡面和理論齒廓的干涉［J］.重慶大學學報:自然科學版，2007，30(5):55-58.

［6］賀鵬，劉光磊.面齒輪傳動安裝誤差特性研究［J］.機械科學與技術，2008，27(1):92-95.

［7］郭輝，趙寧，方宗德，等.基于接觸有限元的面齒輪傳動彎曲強度研究［J］.航空動力學報，2008，23(8): 1438-1442.

［8］LEWICKI D G，HEATH G F.RDS-21 face-gear surface durability tests［C］//AHS International 63rd Annual Forum Proceedings.Virginia Beach:American Helicopter Society，2007:1018-1027.

［9］唐增寶，鐘毅芳.齒輪傳動的振動分析與動態優化設計［M］.武漢:華中理工大學出版社，1994:36-37.

［10］楊振，王三民，范葉森，等.轉矩分流式齒輪傳動系統的非線性動力學特性［J］.機械工程學報，2008，44(7):52-57.