小波變換的時頻分析及其在實際中的應用

徐博堯，楊剛，李欣欣

(中國傳媒大學，北京 100024)

1 引言

在信號分析與系統設計中，Fourier分析得到廣泛應用。在分析方法上，根據信號的時域抽樣定理和頻域抽樣定理，可以將兩種信號的Fourier變換的計算轉換為有限長序列的離散Fourier變換的計算。從而可以從數值上實現對信號的與系統的頻域分析。隨著科學技術的發展和應用領域的擴展，需要對非平穩信號和事變信號進行分析研究，以期獲取信號在不同瞬間對應的頻譜分布，從而了解信號的頻率和能量隨時間變化的規律。但是在利用傅里葉變換分析這些突變信號的時候，無法有效的反映信號在某些瞬間的突變。因為在信號的Fourier變換中，反映的是信號的總體平均信息，信號頻譜中的任一頻率分量都是對信號整個時域定義區間上的Fourier積分或求和，信號在時域上某些瞬間的突變，在信號的頻譜上雖然有所反映，但是一般并不明顯。此外，即使能夠計算出信號的頻譜，但由于信號的瞬間突變而發生了改變，也無法從信號的頻譜中確定信號在時域的突變時刻，即在信號的Fourier變換中，無法反映信號的時間特性。

時頻分析實際上是將一維的時間信號映射到二維的時間尺度上，以便看清在細小時間內信號頻率的變化，這對于非平穩和時變信號來講是非常有用的。

2 小波變換簡介

2.1 綜述

小波分析法是一種非常有效的信號時頻分析方法，在信號處理、語音分析、模式識別等領域有著廣泛的應用。它是一種窗口大小固定，但其形狀可以改變，時間窗和頻率窗都可以改變的時頻局域化分析方法，即在低頻部分具有較高的頻率分辨率和較低的時間分辨率，在高頻部分具有較高的時間分辨率和較低的頻率分辨率，這正符合低頻信號變化緩慢，而高頻信號變化迅速的特點。在大尺度下，可以將信號的低頻信息全局表現出來，在小尺度下，可以將高頻局部特性表現出來因此小波變換被譽為“數學顯微鏡”［1］。總體上說，小波變換比短時傅里葉變換具有更好的時頻特性窗口。對于平穩和非時變信號而言，可以用傅里葉變換分析它的時頻域性質。但是對于非平穩和時變信號來說，傅里葉變換就作用不大了，它無法反映信號在某些瞬間的突變。因為我們需要了解信號在不同瞬間所對應的頻譜分布，從而了解信號的頻率和能量隨時間變化的規律特征。因此我們使用小波變換。小波變換對信號具有良好的自適應性。

2.2 小波變換公式及基本原理

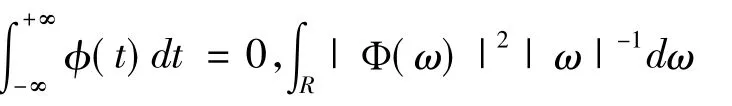
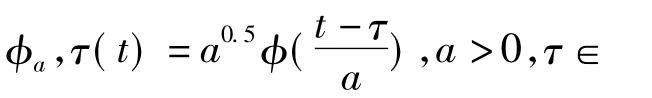
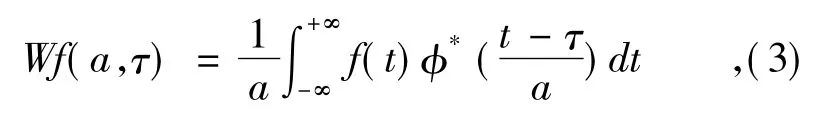
其中a為尺度參數，τ為平移參數。φaτ(t)依賴于a，τ的小波基函數。它們是一組φ(t)經過伸縮平移得到的函數序列。

時頻分析中常用的是連續小波變換，在實際信號處理中常用離散小波變換及其逆變換。連續小波變換表達式為:

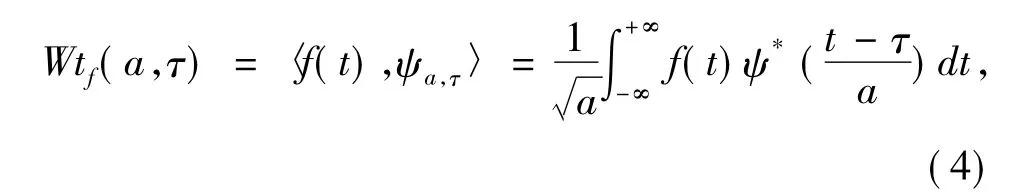
離散小波變換表達式為:

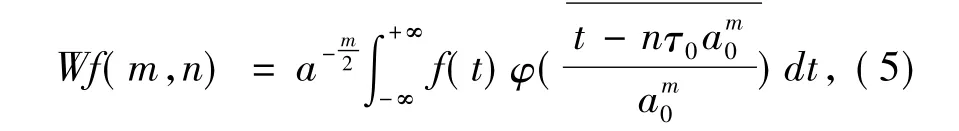
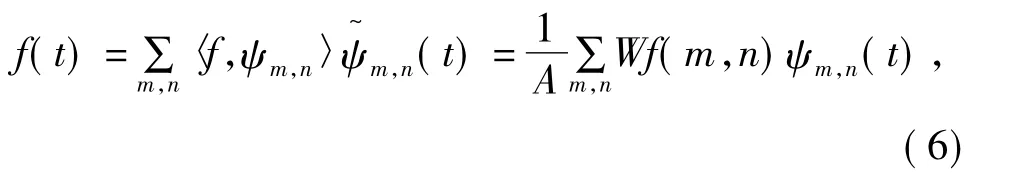
由以上我們可以看出來，小波變換時一種積分變換。小波基并不唯一，即存在許多不同特性的小波基函數，這是它與Fourier變換不同的地方。小波基存在尺度和平移τ兩個參數，所以函數經過小波變換，就可以將一個時間函數投影到時間——尺度平面上，從而同時獲得信號的時間和頻率分量，實現信號的時頻分析［2］。

3 小波變換的時頻分析

3.1 對頻率時變信號做連續小波變換

原信號為一個頻率隨時間增大的函數，其連續小波變換系數如圖1所示。所使用的小波基函數為Daubechies系列的小波基db10。

源程序如下:

wname= ‘db10’;

clear all;

M=2^11;a(1:1:M)=0;

b(1:1:M)=0;

y(1:1:M)=0;

K=400;

Kc=10;

N=10;

L=24;

a(1)=0.5*K;

for i=2:1:M

a(i)=a(i－1)+K;

end

b(1)=Kc+a(1);

for i=2:1:M

b(i)=b(i－1)+(Kc+a(i));

end

for i=1:1:M

y(i)=floor(2^N*cos(2*pi/(2^L)*b(i)));

end

figure(1);subplot(211);plot(y);axis(［0 M，－2^N －100 2^N+100］);

subplot(212);cwt(y，1:1:512，wname，‘plot’);colorbar;

figure(2);subplot(211);plot(y);axis(［0 M，－2^N －100 2^N+100］);

totalscal=512;

wcf=centfrq(wname);

cparam=2*wcf*totalscal;

a=100:－1:1;

scal=cparam./a;

coefs=cwt(y，scal，wname);

f=scal2frq(scal，wname，1/fs);

xlabel(‘時間 t/s’);

ylabel(‘頻率 f/Hz’);

subplot(212);imagesc(t，f，abs(coefs));

title(‘小波時頻圖’);

colorbar;

原信號如圖1中的(a)所示。

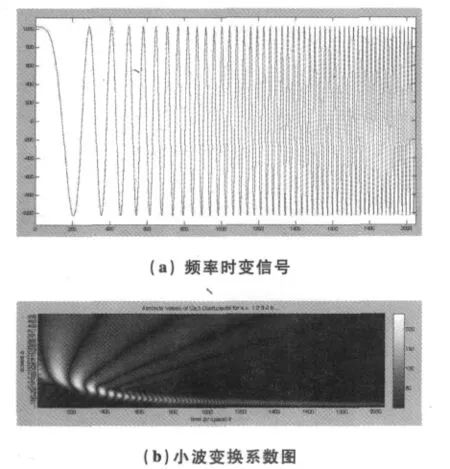
圖1 對頻率漸增信號使用db10小波基函數進行小波變換

從圖1中可以看出來，使用小波變換可以清楚的將信號所包含的頻率成分都識別出來。圖中，亮度高的地方，小波變換系數大;反之則系數小。因此，我們可以看出小波系數大致在時間——尺度上的分布情況［4］。信號在時域的能量等于信號在小波變換域里格展開分量的能量之和，滿足能量守恒。我們還可以看到，隨著原始信號在較低尺度信號空間上的投影，其對應信號的信號分量，相應的平移步長較寬，因而時間分辨率，頻率分辨率逐漸變高，所以如圖所示，信號的高頻分量有了較高的時間分辨率，而信號中低頻分量有了較高的頻率分辨率。這說明，信號的小波變換能夠根據信號的變化特性自動調整時窗和頻窗，因而可以有效的實現信號的時頻分析。

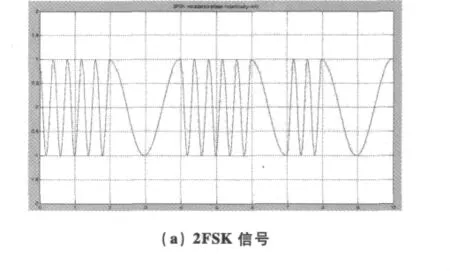
為了更清楚的看清楚不同頻率成分的時間——尺度投影，再給一個只含兩種頻率成分的2FSK信號做小波變換，所選的小波基仍為db10。源程序省略。效果如圖2所示。

從上面可以看出，兩種頻率成分被區分的非常清楚，頻率大小和時間分辨率的關系也在圖中體現出來。

3.2 使用不同小波基對原信號進行時頻分析

小波基的選擇并不是唯一的，這為信號的小波分析提供了更多的靈活性，同時也給實際應用的選擇帶來了一定的難處。下面討論不同小波基分析的時頻效果。

3.2.1 使用 coifl小波基

對原頻率漸增信號使用coifl小波基變換后效果如圖3所示。

3.2.2 使用sym8小波基

對原頻率漸增信號使用sym8小波基變換后效果如圖4所示。

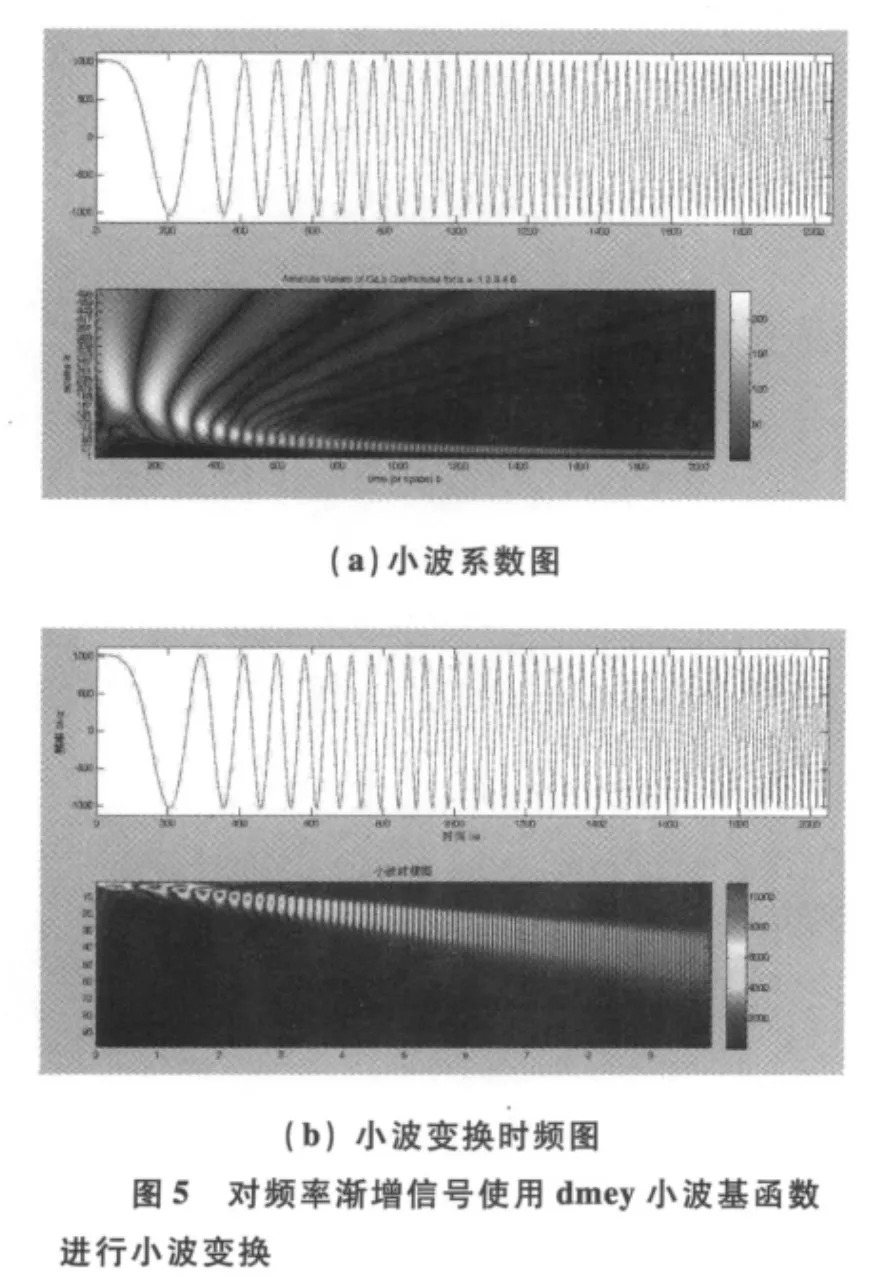
3.2.3 使用dmey小波基

對原頻率漸增信號使用dmey小波基變換后效果如圖5所示。

仔細比較圖1，圖3，圖4，圖5，同一個信號，使用不同的小波基對其進行小波變換，則變換后小波系數不一樣，對高低頻的分辨率也不一樣，出來的時域分辨度也不一樣。小波函數的尺度越高，其對應信號中越精細的細節。因此要根據具體情況適當選擇小波基函數。就原頻率漸增信號而言，選擇db10小波基在所選擇的小波基中是效果最好的。

小波基函數具有非唯一性，它使得小波分析具有更加廣泛的適應性，可實現對于不同特性的信號采用不同的小波基信號，從而使得變換后的小波系數更稀散，更加易于信號的分析和處理。因此，小波分析具有其獨特的優點，特別是對于非平穩信號，有著明顯的優越性。

4 小波變換和其他變換的比較

圖6為原頻率漸增信號經漢明窗的STFT變換后的結果。

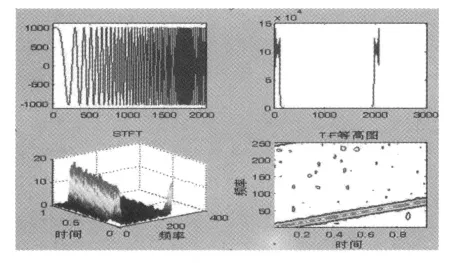
圖6 頻率漸增信號經漢明窗的STFT變換的頻譜、三維、等高圖

小波變換和其他變換一樣，都是將信號展開為一組正交信號的線性疊加。但是Fourier技術是將一維連續變量映射成一維的離散序列;而小波展開則是將一維連續變量映射為而為的離散序列。正式這種二維表示使得小波展開同時具有時間和頻率的分辨率。

如圖6，STFT的時域分辨率和頻域分辨率是相互制約的。STFT變換可以同時具有時頻分辨率，但是其時頻窗口的形狀對于不同的信號分量保持不變。其時間分辨率由信號的STFT中的時窗寬度決定，時窗寬度越窄，時間分辨率越高;頻率分辨率則由窗函數頻譜寬度決定。由窗函數特性可知，窗函數的時域寬度越窄，窗函數頻譜就越窄，因此STFT無法同時獲得較高的時間分辨率和頻率分辨率。而小波變換則能夠對不同信號實現時頻窗口的自動調整。

因此只有小波變換的時頻窗能夠較好的滿足非平穩及時變信號時頻分析的需求。

5 小波變換在實際中的應用

小波分析的應用領域十分廣泛，它包括:數學領域的許多學科;信號分析、圖象處理;量子力學、理論物理;軍事電子對抗與武器的智能化;計算機分類與識別;音樂與語言的人工合成;醫學成像與診斷;地震勘探數據處理;大型機械的故障診斷等方面。

在通信系統中，小波變換最常見的應用有去噪、壓縮和檢測。

下面舉一個小波變換實際應用的例子——小波去噪。仍是給這個時變頻率的原信號加上加性高斯白噪聲，源程序省略。

圖7 利用不同閾值規則給信號進行小波去噪

圖7中分別利用了soft SURE閾值規則、sqtwolog閾值規則、minimax閾值規則進行去噪。

從圖中可見，不同的閾值規則產生了不同的去噪效果。在實際應用中，可以根據具體情況采用相應的閾值規則，以獲得最佳去噪效果。

6 結束語

小波變換和其他形式的Fourier變換相比，在處理非平穩和時變信號上具有明顯的優勢，它能夠根據信號的特性自動調整時窗和頻窗大小，實現信號的時頻分析。在實際應用中，對信號進行小波變換時，選擇小波基函數是難點和重點，需要根據實際情況反復實驗比對方能做出選擇。

［1］ 徐明遠，劉增力.MATLAB仿真在信號處理中的應用［M］.西安:西安電子科技大學出版社，2004.

［2］ STéphane Mallat.陳后金，主編.數字信號處理(第2版)［M］.北京:高等教育出版社，2008.

［3］ 楊力華，戴道清，譯.信號處理的小波引導［M］.北京:機械工業出版社，2002.

［4］ 孫濤，郭亞玲.小波變換在時頻分析中的應用［C］.中國科技論文在線，2006.