基于改進遺傳算法的足球機器人自定位方法*

吳曉

(福州大學機械工程與自動化學院，福建福州350108)

機器人自定位是移動機器人研究中的一個重要課題，是智能移動機器人實現導航、運動規劃等自主能力的基礎，其任務是在具有地圖的環境中，按一定的邊界條件，尋找機器人在起始狀態(包括位置及姿態)和到達目標狀態(包括位置和姿態)時，機器人本身在世界絕對坐標中的位置和姿態［1］.

遺傳算法(GA)模仿生物遺傳及進化的步驟，引入選擇、復制、交叉重組和變異等方法，并將進化論中適者生存的概念引入到算法中，可用于解決諸如控制及函數的優化、機器學習等方面的問題.微觀上，GA是一種隨機算法;宏觀上，它又具有一定的方向性.因此，GA不同于一般的隨機算法，它所使用的隨機選擇是有方向性的，是一個具有定向制導的隨機搜索技術.正因為它的方向性，使得它比一般的隨機搜索算法的效率要高［2］.

全自主機器人足球比賽涉及到諸多關鍵技術，如自定位技術、多任務實時控制技術、實時視覺技術、多機器人協同技術、路徑規劃技術等［3］.其中，機器人自定位問題要求實時性、精確性和魯棒性均要好，是機器人自主化和智能化研究中最為重要的基本問題之一.常用的自定位方法有4類:提取黃、藍球門、立柱等地標點，實現幾何三角定位，由于新規則去掉了黃、蘭門等，現在此方法已不能使用;使用Hough變換等方法提取場地白色標志線并使用球門、立柱信息判斷直線歸屬，實現幾何定位.如Luca［4］提出的利用視覺、聲納、紅外或激光等提供的距離信息，通過Hough變換提取直線再與場地模板比較以確定機器人方位的方法;粒子濾波定位方法，也稱為蒙特卡羅定位方法，如 Menegatti等［5］提出的利用機器人到最近顏色躍變點的距離來對機器人位姿進行估計的粒子濾波算法;基于匹配優化的自定位方法［6］.

以上方法均在過去的機器人比賽中發揮過重要作用，但存在諸如魯棒性不強、實時性不足、實現效率不高、解決不了綁架問題等缺陷［7］.為了更有效解決足球機器人的自定位、綁架和跟蹤問題，文中提出一種基于改進遺傳算法的機器人自定位方法.

1 基于改進GA的機器人自定位方法

遺傳算法是一種全局搜索方法，容易解決綁架問題，同時是一種并行搜索不易陷入局部極值、收斂速度快、處理時間相對較少的算法，具有可擴展性.因而遺傳算法的魯棒性強，高效，全面［8］.基于改進遺傳算法的移動機器人自定位算法步驟如下:

步驟1 初始化進化代數，t=0.

步驟2 生成初始種群.

步驟3 計算t代目標函數.

步驟4 選擇并判斷代溝是否小于某設定值，是則交叉，變異;否則重新選擇.

步驟5 對種群數量進行微分，自適應改變變異概率;t=t+1.

步驟6 判斷總代數，達到總代數則繼續步驟7;否則返回步驟3.

步驟7 估計k時刻機器人位姿，并判斷是否達到軌跡終點，未到則進行步驟8;否則結束.

步驟8 根據位姿跟蹤算法進行跟蹤，得到機器人下一位姿，即下一初始種群，并返回步驟3.

根據機器人比賽運動的實時性、魯棒性要求高，準確性相對要求低的特點，只對遺傳算法的并行搜索、快速收斂和種群優化等方面進行研究.

1.1 編碼

中型組機器人的全向視覺全景圖像是場景通過組合鏡面反射到攝像機得到的.組合鏡面由不同形狀的鏡面組合而成，各部分鏡面分別用于滿足機器人對于相對自身不同方位物體的成像要求.根據足球機器人比賽對視覺系統的要求，文中使用的鏡面由內至外分別為水平等比鏡面、常值斜率鏡面和平面鏡面.其中等比鏡面能使得圖像像素間長度和現實場景中對應點間的長度關系是等比例的，即保持分辨率不變，它能保證6.5 m范圍內水平場地的物體成像是等比例變化的;常值斜率和平面鏡面分別能看到6.5m范圍外的景象，但圖像會產生畸變［9］.

實際坐標和全局坐標的轉化以自定位為中心，定位不成功將導致轉化失去原有的意義.在編碼之前，首先要確定3個坐標系統:圖像坐標系I(u，v)、機器人坐標系R(x，y，z)和世界坐標系W(X，Y，Z).由于足球機器人用的是全向視覺系統，此系統是由攝像機與等比例反射鏡構成的，其觀測范圍是360°，在6.5m半徑范圍內符合針孔成像模型，所以其坐標變換為

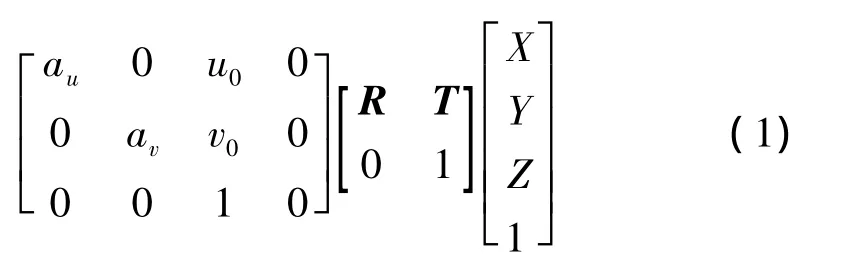
式中，R為旋轉矩陣，T為平移矩陣.另外，由于全向視覺在同一平面上的模型為二維視覺，所以式(1)可以簡化為

則

式中:s為一比例因子;au為u軸上的尺度因子，av為v軸上的尺度因子，(u0，v0)為圖像中心點坐標.(XW，YW，φ)為機器人中心在世界坐標系中的坐標，即機器人自定位坐標;Wj表示第j個觀測點的世界坐標，觀測點在這里特指白線上的特征點(例如1、2、3)，如圖1所示;(uj，vj)為第j個觀測點的圖像坐標;(Xj，Yj)為第j個觀測點的世界坐標.由式(2)可知，機器人自定位參數確定后，直接可根據圖像坐標求出目標的世界坐標.

這里必須特別說明的是:盡管6.5 m以外產生的圖像是畸變的，但當圖像與模型地圖圖1(b)比對時，是不需要“校正”的.這是因為目標函數是求每個“白線點”與模型線間距離總和的最小值，即距離總和小于一常數，所以圖像無需校正，經多次迭代后誤差最小，坐標接近真實值.因此，式(1)和(2)的坐標變換無需校正.

如圖1(a)所示，場地尺寸為12m×8m，按50mm× 50mm柵格的分辨率，分球場模型為24×16個柵格，其中白色標識線含17條直線段和5個圓弧.通過機器人中心發出的輻射線與白線的交點即白線點j，將其作為與模型對應的匹配點.取這些白線點的判據是沿輻射線方向檢測到的顏色按綠－白－綠的次序轉換［10］.

用機器人自定位坐標(XW，YW，φ)的二進制數作為染色體進行編碼，則種群表示為，，i=1，2，…，N，其中N為種群規模，個體編碼為二進制數，如(111100，110010，100000)，表示機器人絕對坐標，解碼后為(600 mm，500 mm，20°);設編碼長度為m，則編碼范圍為［0，2m－1］.

1.2 適應度函數的建立

用dmin，j表示白線點j到場地模型線(共22根)中最近那根線的距離，所有點的最小距離之和為

式中:j=1，2，…，n，n為白線點數 (;Xi，Yi，φi)j表示第i個個體對應第j個觀測點的絕對坐標，可由式(2)根據第i個個體的坐標及全景攝像機的內部參數求得 (;Xi，Yi，φi)jreal表示第j個觀測點所對應地λ表示位于球場外的白線點數，μ表示白線點位于球場外的平均距離誤差，取50cm.這樣，該計算方法可補償噪聲及場地外白線點的影響［11］.圖白線上最近點的絕對坐標.適應度函數為

1.3 初始種群的生成

在對機器人的位姿完全未知或機器人被綁架的情況下，使種群均勻分布在柵格地圖上;否則根據先驗知識給定種群初值，并以已知個別值為中心，按高斯分布給定其它個體的初值.在同一地圖下，種群規模N太大則實時性不強，太小則精度不夠，對于種群規模N的選擇，必須根據定位精度和算法實時性兩方面的要求進行折衷考慮.通常情況下，種群規模應與地圖的大小成正比，否則種群的匱乏易導致定位失敗［12］.合理的選擇為:全景視覺圖像與地圖尺寸成比例的范圍為6 m×6 m，按0.05 m×0.05 m為一個單元柵格，一個單元柵格為一個種群，則有6m×6m÷(0.05m×0.05m)=14400個種群，一般初始種群數為總種群數的百分之一，即N取140.

1.4 遺傳操作設計

1.4.1 選擇

遺傳算法的主要操作為選擇、交叉、變異和終止條件的設定等.選擇的目的是為了從當前群中選出優良的個體，使它們有機會作為父代為下一代繁殖子孫.選擇算子不當會增加群體中相近個體的數量，使得子代個體與父代個體相近，遺傳失去多樣性，產生早熟，導致進化停止.輪盤賭是一種回放式隨機采樣方法，應用比較廣泛，但由于群體規模有限和隨機操作等原因，使得這種選擇方法誤差比較大，有時甚至連適應度較高的個體也選不上.為防止過早收斂，保持群體多樣性，算法的實現基于輪盤賭方法，剔除代溝最大的個體，具體選擇流程如下:

步驟1 隨機產生N個群體;

步驟2 采用輪盤賭的方法進行選擇操作，選出優良子代群體;

步驟3 從子代群體中隨機選取兩個個體i1、i2作為父代;

步驟4 將i1、i2均勻交叉產生子群;

步驟5 計算代溝是否最大，如果最大則轉步驟2，否則選擇操作成功.

1.4.2 交叉

交叉算子是GA中最重要的操作算子之一，實際運行時根據交叉概率Pc進行下一代更新.Pc選得太大容易失去優良的個體，選得大小會降低搜索效率.針對上述問題，文中采用自適應分段概率與均勻交叉相結合的方法進行交叉操作，如式(3)所示，即按適應度值的大小進行排序更新:F1＜F2＜…＜FN，取中間值F3N/4作為分界點，小于F3N/4的適應度個體選用較大的交叉概率，大于F3N/4的適應度個體選用較小的交叉概率.這樣，Pc能夠隨著目標函數適應度值的變化而自動調整，使目標函數適應度值大的個體取較小的Pc，目標函數適應度值小的個體取較大的Pc，從而使適應度值大的優良個體得到保存，而使適應度值小的個體被淘汰.同時適應度高的個體采用單點交叉，適應度低的采用均勻交叉.

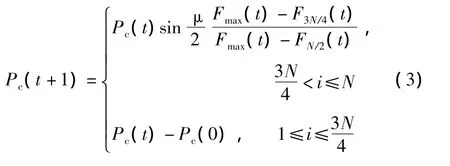
式中，Fmax(t)為最大適應度.

De Jong等［13］已經證明，采用均勻交叉的方法能夠擴大遺傳算子的搜索子空間，使收斂結果更趨于最優解.

均勻交叉會產生一個隨機的掩碼與父代個體等長.若P1、P2表示兩個父代，S1、S2表示兩個子代，M表示掩碼，例如，對于S1，當掩碼中的位為1時，S1的對應位為P2的對應位，S2的對應位為P1的對應位;當掩碼中的位為0時，S1的對應位為P1的對應位，S2的對應位為P2的對應位，即掩碼為1則交叉，為0則不變.例如:

1.4.3 變異

變異操作主要用來改善遺傳算法的局部搜索能力和維持群體的多樣性，防止出現早熟現象.自適應有效基因突變的特點是最低有效基因個數自適應變化，且自適應調整變異概率Pm.Srinivas等［14］提出根據每代個體適應度的改變，自適應地改變Pc和Pm，在保護最優個體的同時，加快了較差個體的淘汰速率.

式(4)中，采用最大適應度Fmax、最小適應度Fmin、適應度平均值Fave來衡量群體適應度的集中程度，自適應地改變整個群體的Pm.其中，Fmin和Fmax的接近程度反映了整個群體的集中程度，二者越接近，遺傳算法越可能陷于局部最優解，即越可能早熟.ε1、ε2為大于零的常數，σ2(t)為個體適應度的方差.

采用如下的自適應原則改變Pm:當機器人受到綁架時，調整概率的突變.實驗表明，當機器人發生綁架時，種群的個體適應度會急劇下跌，即當 Fave時，自動增加Pm(t+1)值.當陷入早熟時，即σ2(t)≤ε2時，自動調整Pm.除上述情況外，Pm(t+1)=Pm(t).

1.5 控制參數的選擇

遺傳算法控制參數的選擇十分關鍵，選取不同的控制參數會影響算法的性能和整個算法的收斂性.這些參數包括群體規模N、選擇常數q、二進制編碼長度、變異概率Pm、交叉概率Pc等.

交叉概率大可使各代充分交叉，但群體中的優良模式也易遭到破壞，產生代溝，使搜索走向隨機化;交叉概率太小，復制增加搜索會陷入停滯狀態.變異算子增加了群體的多樣性，防止遺傳算法過早收斂到局部最優.但變異概率過大時，搜索會產生隨機化;過小時，一旦陷入局部極值則很難跳出來，易產生未成熟收斂.

交叉運算是GA區別于其它進化運算的重要特征，是產生新個體的主要方法，屬全局搜索;而變異運算是GA產生新生個體的輔助方法，屬局部搜索.交叉概率Pc一般選0.40～0.99;變異概率Pm一般選0.0001～0.1000.

群體規模的大小直接影響到GA的收斂性和計算效率，規模過大則搜索效率會降低，規模過小則容易收斂到局部最優解.根據實際情況，群體規模一般選擇10～200.

1.6 位姿跟蹤

在進行若干代更新后，個體收斂到最佳值，可以求得機器人的自定位世界坐標值，但為了增加自定位坐標的魯棒性，這里采用加權平均的方法，即對最佳個體的前3名求平均值，將其作為機器人的估計坐標:

式中，i'表示按自適應度排序后的個體序號，k'表示進化結束的時刻.

由于機器人是連續定位的，在k+1時刻的自定位可以通過重復k時刻的步驟求得，也可以在k時刻自定位的基礎上，利用其位姿的估計信息結合里程計運動信息和觀測信息的導數求得:

式中:ΔXW、ΔYW和Δφ為選取的步長;觀測點的絕對坐標為(X，Y)，第j個白線點的絕對坐標Wj可直接由式(2)求得，那么觀測點與真實點的距離誤差為f(X，Y).按Prewitt算子計算梯度，則

其中，

另外，假設觀測數據符合高斯分布［15］.

圖1 足球場地及坐標Fig.1 Soccer field and coordinate

2 仿真與實驗結果分析

2.1 仿真結果與分析

試驗的軟、硬件條件為:Window XP操作系統平臺，VC++6.0環境下編程;酷睿雙核筆記本電腦.

為驗證改進遺傳算法的有效性，通過兩組仿真的白線點數據進行算法驗證，主要過程是機器人經歷從綠(圖2(a)下部點)到紅(圖2(a)上部點)的移動過程，直接用給定的白線點坐標代替全景白線點數據，為了表達的真實性，在給定的白線點坐標中加入觀測噪聲，其符合正態分布N(0，0.02(x，y))，步長為(0.05，0.05，0.1).圖2(a)所示為預先設定的規則輻射線與白線圖像框的交點(白線點)，若機器人的自定位坐標設定為(0，0，0)、(－0.1，0.15，0.05)、(－0.5，8，μ/6)，則可直接求出各白線點的相對位置坐標.反過來以各白線點的相對位置坐標為參數，用上述遺傳算法迭代求出機器人的自定位坐標，分析與設定坐標的誤差，并與蒙特卡羅定位法比較，過程為由綠點到紅點.然后再按圖2(b)所示，以隨機選取的已知白線點的相對坐標為參數，用遺傳算法與蒙特卡羅定位法再次比較，過程為黃點－(圖2(b)下部點)到白線點(圖2(b)上部點).

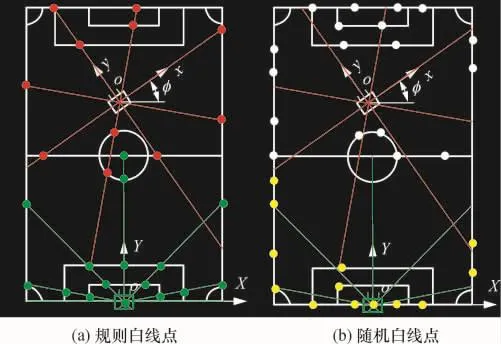
圖2 實驗數據示意圖Fig.2 Diagram of experimental data

采用全局搜索，種群數為50，初始值為與視覺圖像成比例的6.5m范圍內的方位值，選擇參數q= 0.5，步數為50，初始交叉概率為0.8，初始變異概率為0.07，終止條件為適應度函數值大于95%.當迭代次數大于總次數的25%而適應度函數差分小于10%時，個體值置位重新計算，以避免進入局部最優.結果如表1、2所示，其中a為一組具備直線特征的數據，b為一組模擬的隨機數據.從表1中可知，采用遺傳算法連續自定位的誤差遠小于采用蒙特卡羅算法產生的誤差，其中隨機白線點產生的自定位誤差又小于輻射線上白線點的自定位產生的誤差.

表1 自定位實驗數據Table 1 Test results of self-localization %

表2 綁架實驗數據Table 2 Test results of kidnapping %

在綁架仿真過程中，突然改變機器人坐標所對應的白線點數據，相當于在實戰中的機器人被綁架.從表2中可以看出，綁架后的自定位誤差比連續自定位的誤差有所增加，但通過連續迭代趨于收斂，完全能夠滿足機器人的自定位需求.

由于蒙特卡羅算法與遺傳算法在實際操作中都是以統計概率或隨機數據為依據，所以隨機參數取得的白線點自定位總是更有效，但在機器人比賽實踐中，隨機白線點是無法求得的，只有求輻射線上的白線點或有規律的白線點，才有可能進行應用操作.

2.2 實驗結果與分析

針對上述遺傳算法，采用地圖為12 m×8 m的標準足球比賽實驗場地進行足球機器人實驗驗證.為了提高算法的實時性，以50mm×50 mm為一單元柵格，分地圖為24×16個單元柵格.遺傳算法的種群初始化、選擇、交叉、變異操作及適應度的計算等步驟均基于柵格地圖進行.

為說明算法的性能，比較了相同參數下采用傳統遺傳算法和改進遺傳算法進行分析的結果.算法的參數為:初始化種群大小為50，q=0.5，Pc=0.8，Pm=0.01.經過80代進化后最小誤差變化曲線見圖3.由圖3可看出，改進遺傳算法的最小誤差變化曲線收斂得更快，求解自定位坐標和尋優效率均優于傳統遺傳算法，更有利于產生最優解.

圖3 最小誤差變化曲線Fig.3 Change curves of minimum error

在實驗中，假設機器人初始位姿為絕對坐標原點(圖2中“O”)，在機器人自由運動后能夠實現全局定位.為了模擬“綁架”現象，當機器人運行到第40步時，將被人為轉移到一個未知位姿，前后位姿之間的實際變化量為(－1.3m，+4m，μ/6).這就要求機器人能夠發現“綁架”現象，并能從中恢復，正確實現全局重定位.“綁架”發生后機器人繼續進行正常比賽.改進的遺傳算法與蒙特卡羅算法的結果比較見圖4.從圖4中可看出，改進的遺傳算法在起步階段有較快的收斂速度，在11步內實現機器人的快速全局定位;在第40步遭遇機器人“綁架”時，該算法也能夠迅速收斂，快速實現機器人的重定位;在定位過程的其它階段，算法具有較高的平均位姿跟蹤精度，其平均跟蹤誤差約為(0.046m，0.22°);且改進的遺傳算法的定位精度較高.

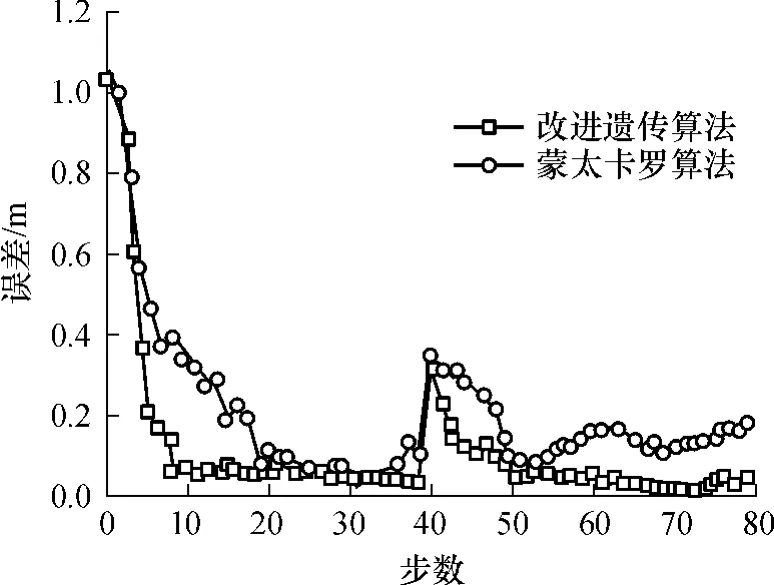
圖4 定位誤差曲線Fig.4 Curves of localization errors

由上述結果可以看出:(1)改進遺傳算法與傳統遺傳算法相比，其對目標函數的收斂速度快，魯棒性好，同步數目標誤差更小;(2)改進遺傳算法與蒙特卡羅算法相比，收斂速度快，平穩無震蕩且定位誤差更小，且在被人為綁架后能夠更快速地自定位; (3)仿真輻射線、綁架輻射線自定位精度分別達到98.74%和96.58%，仿真隨機白線點、綁架隨機白線點自定位精度分別達98.98%和96.92%.(4)與文獻［6］、［15］中結果相比，其多組實驗自定位平均誤差基本在0.059～0.390m和2.5°～4.2°，而文中平均跟蹤誤差約為(0.046m，0.22°).

3 結語

文中針對足球機器人在比賽過程中的自定位問題進行了分析.利用改進遺傳算法，以白線點為參數進行自定位坐標的求取，通過仿真實驗與實地驗證，發現采用改進遺傳算法進行全局自定位高效、魯棒，局部梯度搜索快速、精確;采用改進的遺傳算法進行移動機器人的自定位收斂速度快，11次迭代便達到了較高的定位精度;在足球場地實驗中，當人為綁架機器人后，能夠在11步之內快速實現重新自定位，從而證明了該算法在連續定位和綁架情況下的自定位均能滿足足球機器人比賽的要求，為機器人的自定位提供了一種新方法.

［1］ Lu H M，Zhang H，Xiao J H，et al.Arbitrary ball recognition based on omni-directional vision for soccer robots［C］∥RoboCup 2008:Robot Soccer World Cup XII.Berlin:Springer-Verlag，2009:133-144.

［2］ Chang P，Chen S H，Liu C H.Sub-population genetic algorithm with mining gene structures for flow shop scheduling problems［J］.Expert Systems with Applications，2007，33 (3):762-771.

［3］ Melville P，Mooner J.Creating diversity in ensembles using artificial data［J］.Information Fusion，2005，6(1): 99-111.

［4］ Luca Iocchi.Robust color segmentation through adaptive color distribution transformation［C］∥Advances in Cryptology Crypto 91.Berlin-Heidelberg:Springer-Verlag，2006: 287-295.

［5］ Menegatti E，Pretto A，Scarpa A，et al.Omnidirectional vision scan matching for robot localization in dynamic environments［J］.IEEE Transactions on Robotics，2006，22 (3):523-535.

［6］ 盧惠民，張輝，楊紹武，等.一種魯棒的基于全向視覺的足球機器人自定位方法［J］.機器人，2010，32(4): 553-559.Lu Hui-min，Zhang Hui，Yang Shao-wu，et al.A robust self-localization method based on omnidirectional vision for soccer robots［J］.Robot，2010，32(4):553-559.

［7］ 盧惠民，劉斐，鄭志強.一種新的用于足球機器人的全向視覺系統［J］.中國圖象圖形學報，2007，12(7): 1243-1248.Lu Hui-min，Liu Fei，Zheng Zhi-qiang.A novel omni-vision system for soccer robots［J］.Journal of Image and Graphics，2007，12(7):1243-1248.

［8］ 劉建立，左保齊.基于遺傳算法的織物印花圖案的分割［J］.計算機工程與設計，2008，29(15):3966-3967.Liu Jian-li，Zuo Bao-qi.Segmentation of pattern of printed fabric based on genetic algorithm［J］.Computer Engineering and Design，2008，29(15):3966-3967.

［9］ 劉偉.RoboCup中型組機器人全景視覺系統設計與實現［D］.長沙:國防科技大學機電工程與自動化學院，2004.

［10］ 吳曉，曹其新.基于權值模板匹配算法的全自主足球機器人目標識別［J］.廈門大學學報:自然科學版，2008，47(6):819-822.Wu Xiao，Cao Qi-xin.Target Recognition of an autonomous robot soccer based on weight template matching algorithm［J］.Journal of Xiamen University:Natural Science，2008，47(6):819-822.

［11］ Weiss C，Masselli A，Tamimi H，et al.Fast outdoor robot localization using integral invariants［C］∥Proceedings of the 5th International Conference on Computer Vision Systems.Bielefeld:Applied Computer Science Group，2007.

［12］ 賀鋒，秦曉麗，方勇純.一種基于遺傳算法的移動機器人自定位方法［J］.模式識別與人工智能，2009，22 (1):142-147.He Feng，Qin Xiao-li，Fang Yong-chun.A genetic algorithm based autonomous localization strategy for mobile robots［J］.Pattern Recognition and Aritificial Intelligence，2009，22(1):142-147..

［13］ De Jong K A，Spears W M.A formal analysis the role of multi-point crossover in genetic algorithms［J］.Mathematics and Artifical，1992，5(1):1-26.

［14］ Srinivas M，Patnaik L M.Adaptive probabilities of crossover and mutation in genetic algorithms［J］.IEEE Transactions on System，Man and Cybemeties，1994，24 (4):656-667.

［15］ Heinemann P，Haase J，Zell A.A novel approach to efficient Monte-Carlo localization in RoboCup［C］∥Robo-Cup 2006:Robot Soccer World Cup X.Berlin，Germany: Springer-Verlag，2007:322-329.