一種基于最大最小特征值的協同頻譜檢測算法

康安康， 何 斌

（1.秦皇島91404部隊，河北秦皇島 066000; 2.中國科學院長春光學精密機械與物理研究所，吉林長春 130033）

0 引 言

隨著從單一的語音通信向無線多媒體以及Web類型應用的轉變，對更高數據率的需求正不斷增加。然而，目前留給新系統、業務和技術的頻譜非常少，甚至沒有頻譜可以分配。可用頻譜的匱乏已經成為制約無線通信新技術發展的最大障礙。

認知無線電作為一個解決頻譜擁擠問題的嘗試而出現。自1999年瑞典的Jeseph Mitola[1]博士提出認知無線電的概念以來，認知無線電迅速成為無線通信領域的研究熱點。認知無線電技術成為解決目前頻譜資源緊張的有效手段。

當前許多新的單節點頻譜感知方法陸續被提出。文獻[2]提出了一種寬帶多步頻譜檢測方法，該方法將整個的頻譜檢測工作分為兩步進行，即粗檢測方法和細檢測方法;文獻[3]提出了一些基于GLRT（廣義似然比檢驗）的有效頻譜感知方法。單節點的最大最小特征值檢測法[4-5]（Maximum and Minimum Eigenvalue，MME）是由新加坡電信研究院提出的。這種算法同能量檢測一樣具有復雜度低，不需要先驗信息的優點，同時還能克服噪聲不確定性的影響。文中在分析了上述方法的基礎上，提出了一種基于最大最小特征值加權的協同頻譜感知算法。該算法保持了單節點MME算法的優點，并且進一步提高了檢測概率。

1 系統模型

在基本的發射機端檢測中，系統模型[6]如下:

1）H0:接收信號只存在噪聲（沒有發射信號）;

2）H1:接收信號中同時存在信號和噪聲。

式中:ηi——噪聲，這里假設N個樣點上疊加的都是獨立同分布的高斯白噪聲，且ηi～N（0，σ2）;

xi——授權用戶信號的第i個樣點，表示認知用戶檢測到的第i個信號;

h——信道增益。

對于各參與感知的節點，假設信號是數字調制并且為過采樣的。設s（n）為數字調制的源信號，并且定義其符號周期為T0，通過濾波和傳輸信道得到的信號為:

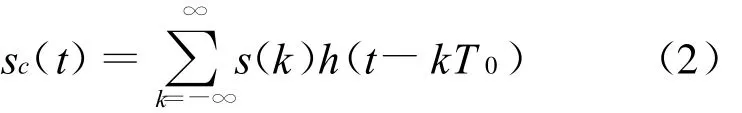
其中，h（t）由發射濾波、信道響應和接收濾波共同作用形成。假設h（t）具有有限支撐[0，Tu]。假設接收信號為過采樣的，并且過采樣因子為M，即采樣周期為:

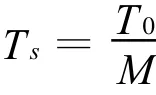
定義:

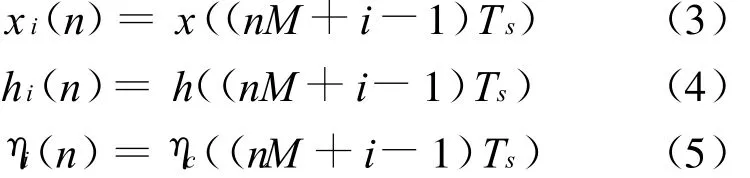
式中:n=0，1，…;i=1，2，…，M。

可以得到:

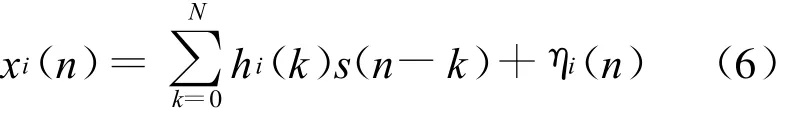
式中:N=Tu/T0。

則構成采樣矩陣表達式為:

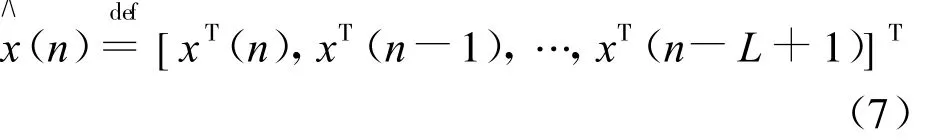
即:

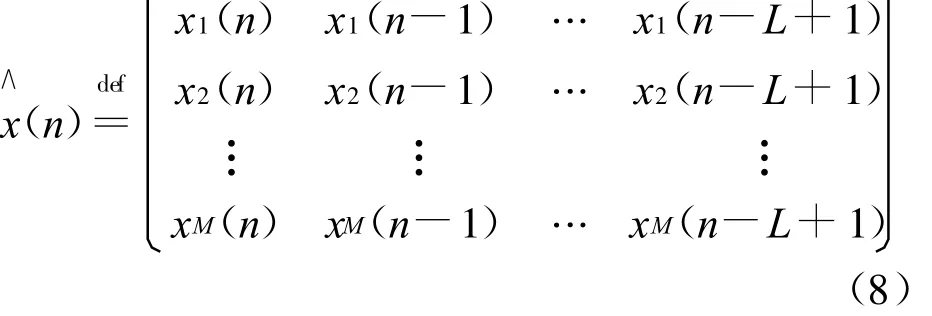
2 加權系數的選擇

采用數據融合方法中的軟判決算法，對各單節點檢測的最大最小特征值進行加權與判別闕值進行比較，從而判斷信號的存在性。因此，加權系數的選擇成為重點。

2.1 信號因素

電磁波在自由空間內傳播發生的能量損耗，考慮到天線輻射的方向性、接收與發射天線的極化特性匹配情況等因素，假定接收天線處于最佳接收狀態下，在距離發射天線d處，接收天線的接收功率[7]表示為:

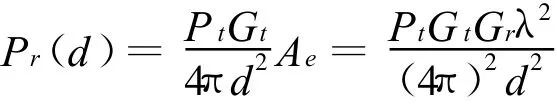
式中:Pt——發射功率;

Gt——發射天線增益;

Gr——接收天線增益;

λ——電磁波波長，m;

d——接收機與發射機之間的距離。

自由空間中，信號從發射機到接收機只沿一條路徑傳播。現實環境中，特別對于移動通信傳播環境，由于傳播路徑上存在各種不同類型和尺寸的地物，這些地物對電磁波的反射、散射和吸收是普遍存在的，因此，無線電波傳播的功率衰減比自由空間中的速率 d-2快得多，在室外一般取d-4。

2.2 噪聲因素

傳感器網絡中，有一種最優加權方法[8]，它的原理是基于能量檢測的，因此在頻譜檢測中也同樣適用，其推導的估計表達式的均方誤差為:

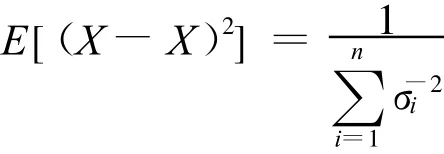
3 算法實現

通過第2節的分析可以得出以下結論，從信號和噪聲方面考慮，加權系數可以用主用戶與子節點之間的距離d和噪聲功率來表示，距離衰減通常采用d-4，因此，文中采用d-4來表示信號功率因素。

加權系數表示為:

式中:di——子節點i到主用戶的距離;

由以上分析可以得出特征值比值融合的CMME算法實現步驟如下:

1）各子節點進行L點信號采樣并發送至主節點，構成采樣數據矩陣;

2）記R（NS）為收到信號的樣本協方差矩陣，根據步驟1）的采樣數據矩陣計算得出協方差矩陣:

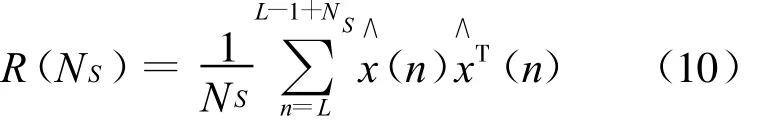
3）計算協方差矩陣R（NS）的最大最小特征值比值θi;

4）根據

計算判別闕值γ;

5）各子節點將計算所得的最大最小特征值比值θi發送至主節點;主節點按照各子節點加權系數計算加權后的特征值比值，計算方法如下:

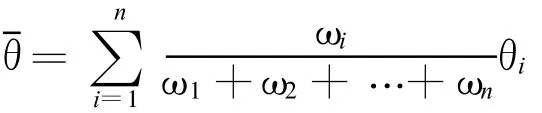
式中:n——子節點總數;

6）按照下面規則判決:

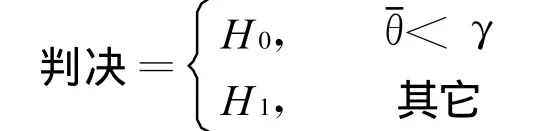
式中:H0，H1——分別為信號不存在和信號存在的情況。

4 仿真與分析

仿真了節點采樣點數為1 000和2 000的情況下，最大最小特征值比值融合的協同頻譜感知方法的檢測概率隨信噪比變化的曲線，分別如圖1和圖2所示。

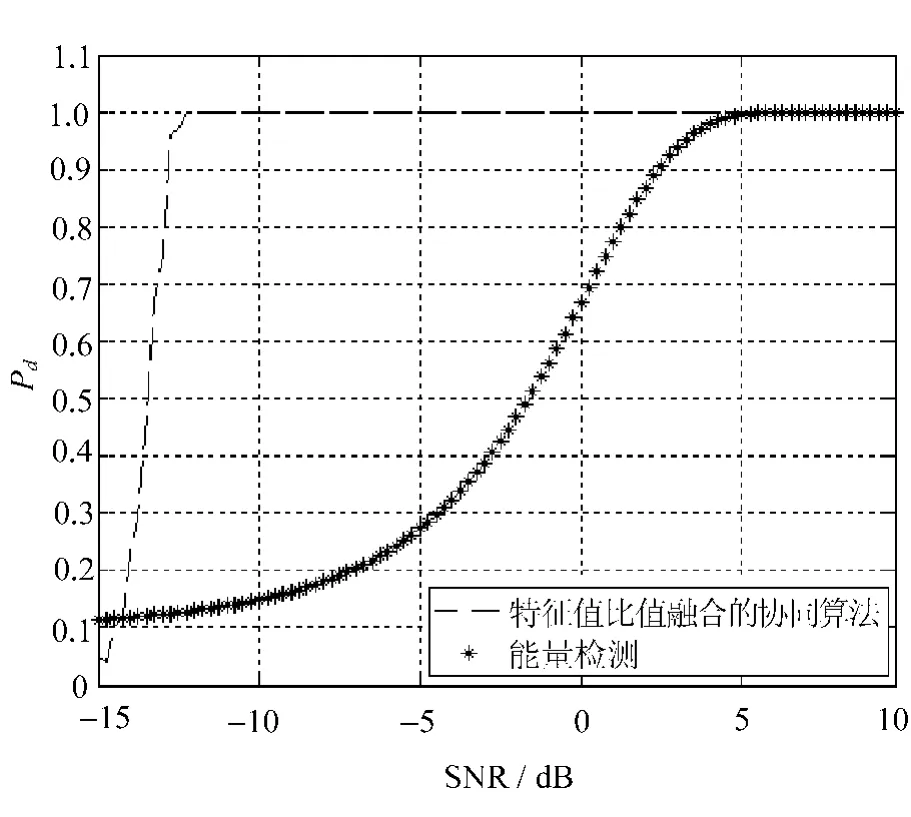
圖1 采樣點數為1 000的CMME算法性能仿真圖

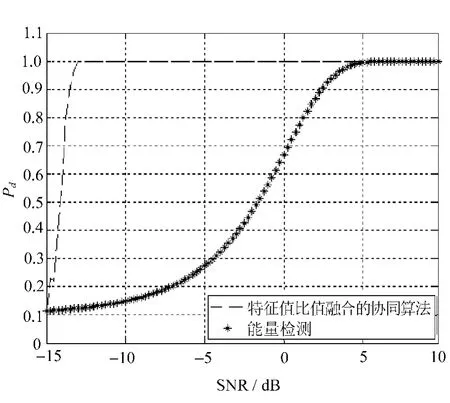
圖2 采樣點數為2 000的CMME算法性能仿真圖

仿真環境設定各子節點虛警概率為0.10，能量檢測虛警概率也為0.10，信噪比范圍是-15～9.75 dB。

從圖中可以看出，能量檢測在信噪比達到5 dB以后，檢測概率才達到100%，而采樣點數分別為1 000和2 000的最大最小特征值比值融合方法的檢測概率在-12 dB以下時，即開始收斂至100%，其中，采樣點數為1 000的曲線比采樣點數為2 000的曲線更快地收斂到1。

在和能量檢測對比情況上（見圖2），兩條曲線都收斂于1之前，采樣點數為2 000的最大最小特征值比值融合的感知方法的仿真曲線一直在能量檢測曲線之上，即其檢測效果要遠遠好于能量檢測。圖1中所示的兩條曲線中，在低信噪比情況下，采樣點數為1 000的最大最小特征值比值融合的感知方法仿真曲線有一小段在能量檢測之下，其檢測效果比能量檢測的效果要差，這也說明了各子節點的采樣點數Ns對最大最小特征值比值融合的感知方法有著很大的影響，當采樣點數越多時，信號檢測概率也就越大。

下面從接收機操作特性曲線（ROC）方面比較新算法與能量檢測算法的優劣。接收機操作特性曲線是在一定的信噪比情況下，虛警概率與檢測概率的關系曲線，文中的新算法ROC曲線是在SNR=-15 dB的情況下得到的，能量檢測算法是在SNR=-3 dB情況下得到的。3個檢測節點的SNR值都為-15 dB的情況下，特征值比值融合的協同感知方法與能量檢測算法比較如圖3所示。

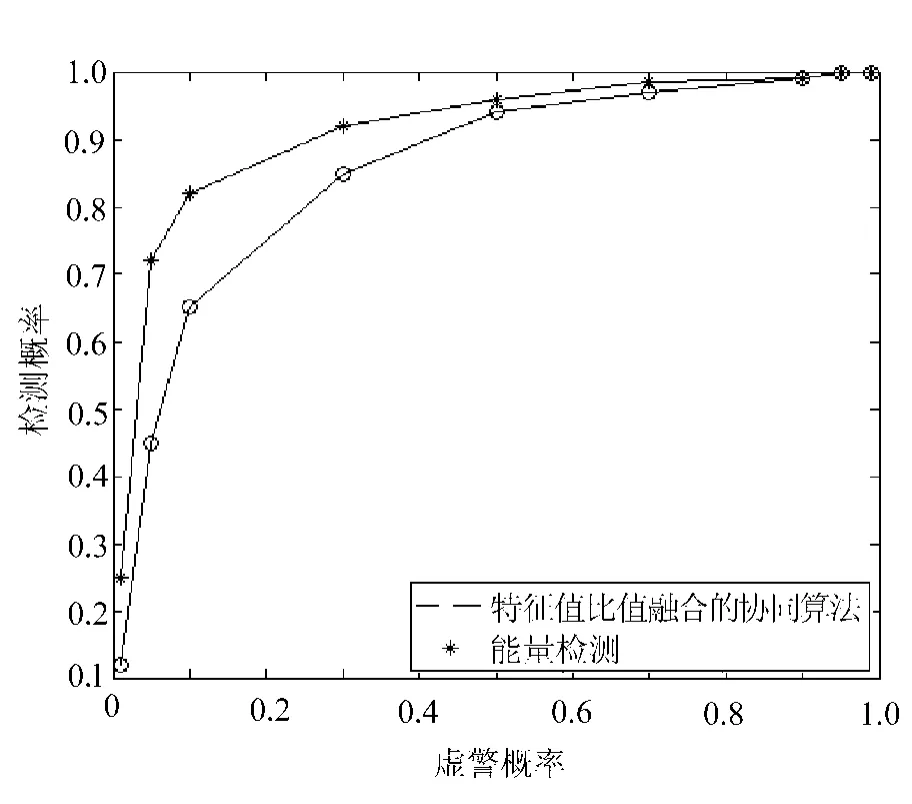
圖3 接收機操作特性曲線

圖中，基于特征值比值融合的協作頻譜感知算法的不同檢測概率和虛警概率是通過改變γ因子得到的，而能量檢測算法不同的虛警概率和檢測概率是通過改變單節點的能量檢測的判決門限值得到的。從圖中可以看出，在一定的虛警概率下，文中提出的檢測算法的檢測概率要高于能量檢測的檢測概率，檢測性能比能量檢測算法有很大的提高。

5 結 語

提出了一種基于最大最小特征值比值融合的協同檢測算法，該算法繼承了單節點最大最小特征值算法不需要先驗信息，同時還能克服噪聲不確定性影響的優點，也進一步提高了檢測概率。仿真證明，該算法與能量算法相比具有很大的優越性。

[1] Rieser C J.Biologically inspired cognitive radio engine model utilizing distributed genetic algorithms for secure and robust wireless communications and networking[D]:[Ph D Thesis].Augest:Virginia Tech，Blacksburg，VA，2004.

[2] Lim T J，Zhang R，Liang Y C，et al.GLRT-based spectrum sensing for cognitive radio[C]//IEEE GlobeCom.New Orleans，USA:[s.n.]，2008.

[3] 朱江.頻譜感知算法及授權用戶用頻行為研究[D]: [碩士學位論文].武漢:華中科技大學，2010.

[4] Zeng Y H，Liang Y C.Maximum-minimum eigenvalue detection for cognitive radio[C]//The 18th IEEE Intern.Symposium on Personal，Indoor and Mobile Radio Communication Proceedings.Athens Greece:[s.n.]，2007.

[5] Zeng Y H，Liang Y C.Eigenvalue based spectrum sensing algorithms for cognitive radio[C]//IEEE Institute for Info Comm Research.November:[s.n.]，2009.

[6] 石磊.認知無線電中空閑頻譜檢測技術的研究[D]: [碩士學位論文].哈爾濱:哈爾濱工業大學，2010.

[7] 周文安.無線通信原理與應用[M].北京:電子工業出版社，2006.

[8] 景博，孫勇.基于集中式最優加權算法的多傳感器數據融合[J].電子測量與儀器學報，2004（s4）: 1143-1147.