二階串聯諧振系統Matlab/Simulink仿真

陳 雪

（太原師范學院物理系，山西太原 030031）

0 引 言

信號與系統分析在電子與信息領域中占據著重要的地位[1-2]。傳統的理論分析方法是通過數學方法建立方程求解而得出分析結果，需要大量的數學運算。而在現代工程中，隨著計算機技術和仿真軟件的發展，人們通常利用仿真技術建立數學模型，對實際系統進行模擬，分析不同的信號輸入和系統參數改變時系統響應或性能的變化[3]。Simulink作為Matlab的工具箱之一，是交互式動態系統建模、仿真和分析的圖形環境，在信號處理領域得到了廣泛應用[4-8]。

文中以RLC二階串聯諧振系統為例，利用Simulink動態仿真軟件建立了電路形式和框圖形式的兩種仿真模型，而這兩種模型，都可以直觀方便地顯示系統回路的電流響應曲線。通過模擬仿真可以看到，將Matlab運用到信號與系統的分析中，不但簡化了大量的數學運算，而且使系統分析更為簡便高效。

1 二階串聯諧振系統的建模

RLC二階串聯諧振系統是連續系統分析的典型研究對象，理論上經常討論此系統有關回路電流i（t）為響應的問題。文中選取電路參數L= 1 H，C=1 F，用ω=1 rad/s的正弦信號作為激勵e（t），首先建立系統的數學模型。根據基爾霍夫電壓定律，可建立回路方程

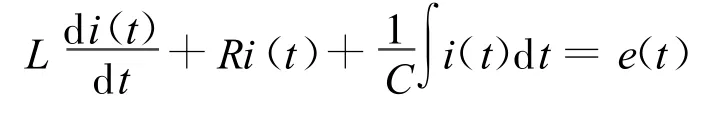
方程左右兩邊分別求導，得

對上述方程左右兩邊進行拉式變換，并求得系統函數

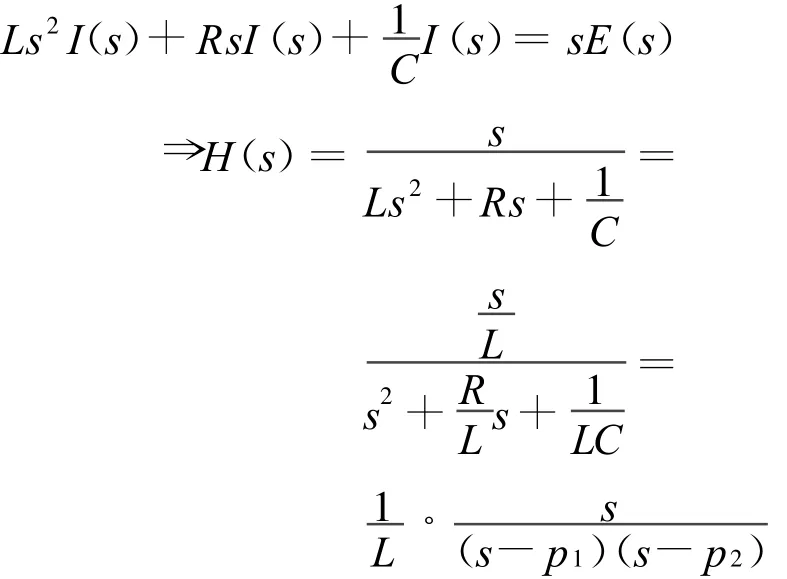
其中，極點位置是

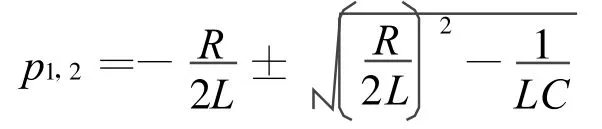
2 基于Simulink的二階串聯諧振系統仿真分析

2.1 電路模型仿真

運用Simulink可以建立二階串聯諧振系統的電路模型，如圖1所示。

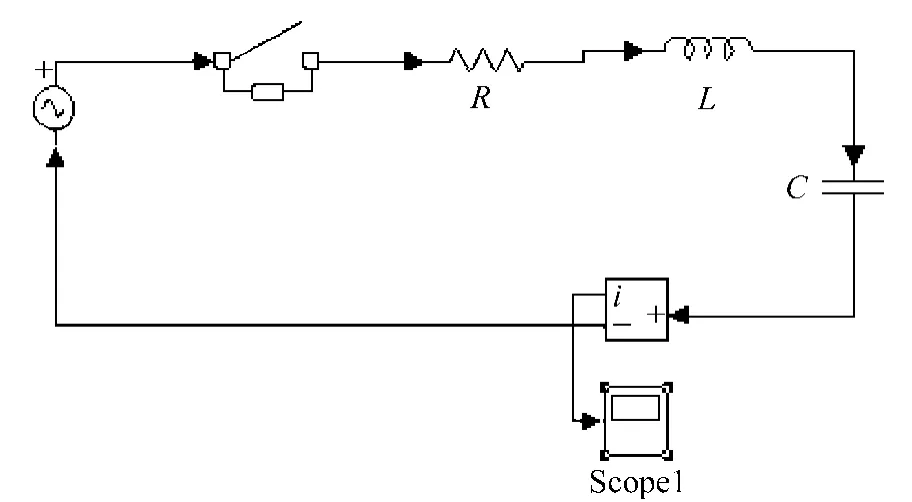
圖1 基于Simulink的二階串聯諧振系統電路模型

模型中用ω=1 rad/s的正弦信號作為激勵，通過改變電阻的阻值可以改變衰減因子α的取值，從而可以直觀地觀察不同損耗時的系統i（t）波形。

RLC無損系統（α=0）的i（t）波形如圖2所示。

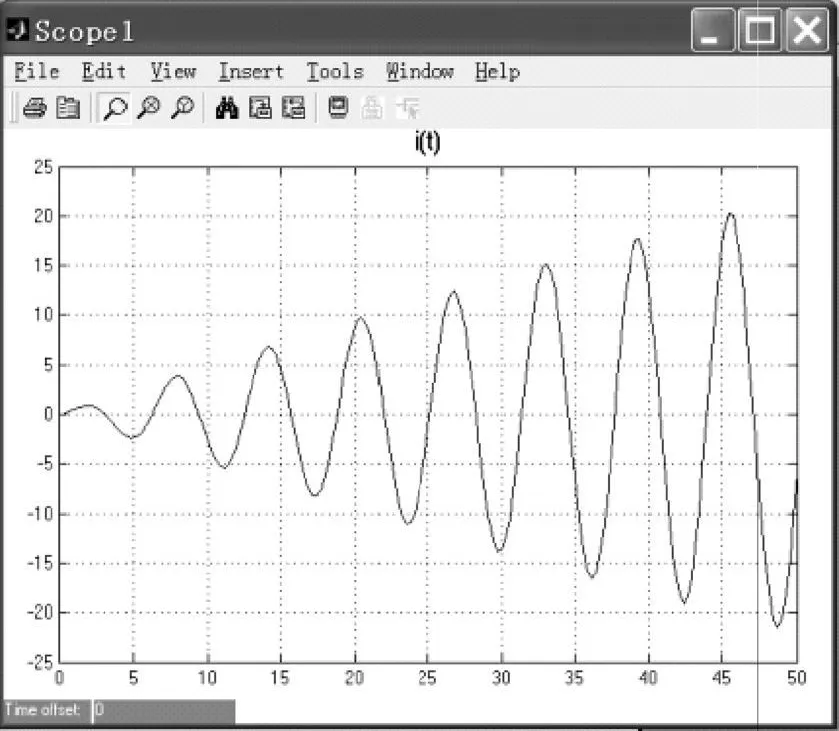
圖2 α=0時無損電路正弦激勵電流響應

由圖可見，由于電路發生了諧振，它的包絡為線性增長的同頻正弦信號。

另外，通過改變衰減因子α的值，可以更直觀地去研究系統正弦穩態過渡過程。同信號激勵RLC有損系統（α=0.25，α=1）的i（t）波形如圖3和圖4所示。

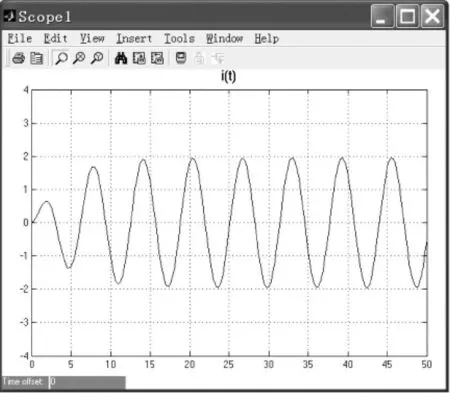
圖3 α=0.25時有損電路正弦激勵電流響應

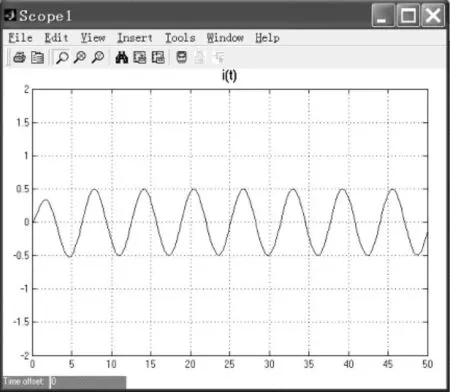
圖4 α=1時有損電路正弦激勵電流響應

可見隨著t的增大，i（t）中的暫態響應迅速結束，電路很快進入正弦穩態。

2.2 系統模型仿真

為了對線性時不變（LT I）系統進行分析，需要首先建立與系統相對應的系統函數。以α=1的二階串聯諧振系統為例，取電路參數L=1 H，C=1 F，R=2 Ω，建模后其系統函數可以表示為:

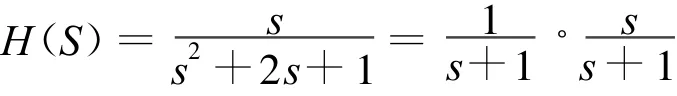
根據梅森公式，上式的分子可以看作是1條前向通路的增益，分母可以看作是2個回路組成的特征行列式，而且各回路都互相接觸，由此可以構建系統模型。在Matlab/Simulink運行環境中選擇相應的模塊，在model板上構建出系統模型，設置相應的參數進行仿真，用直接型和級聯型實現的二階串聯諧振系統模型分別如圖5和圖6所示。

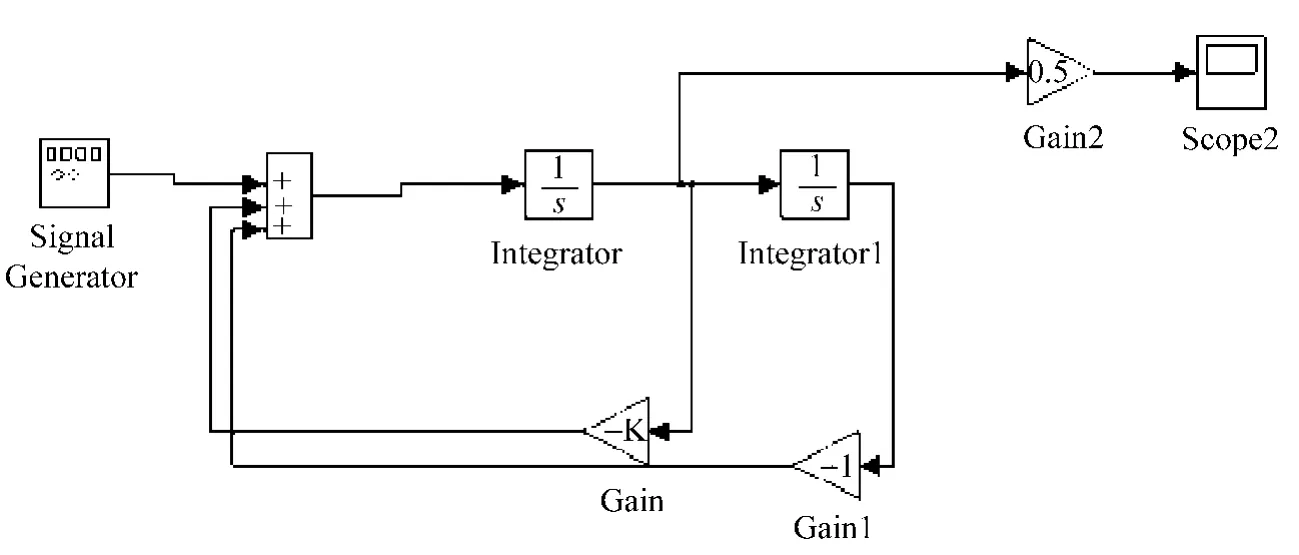
圖5 基于Simulink的直接型二階串聯諧振系統模型

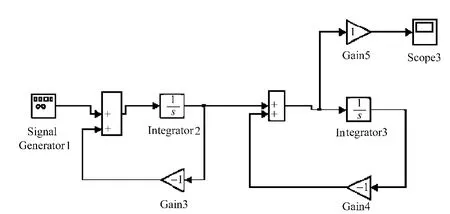
圖6 基于Simulink的級聯型二階串聯諧振系統模型

雙擊示波器scope顯示正弦激勵信號的電流響應結果如圖7所示。

通過與圖4比較發現，利用系統函數建立的系統模型與實際的電路仿真得到的響應是一致的，體現了利用Simulink進行二階串聯諧振系統建模的準確性。

3 結 語

以RLC二階串聯諧振系統為例，分析了線性時不變系統的建模方法。并利用Simulink動態仿真軟件建立了電路形式和框圖形式的兩種仿真模型，而這兩種模型都可以直觀方便地顯示系統回路的電流響應曲線。通過模擬仿真可以看到，將Matlab運用到信號與系統的分析中，不但簡化了大量的數學運算，而且使系統分析更為簡便高效，對理論研究和工程應用都具有重要意義。

[1] 鄭君里，應啟珩.信號與系統[M].2版.北京:高等教育出版社，2004.

[2] 吳大正.信號與線性系統分析[M].3版.北京:高等教育出版社，2003.

[3] 姚俊.Simulink建模與仿真[M].西安:西安電子科技大學出版社，2005.

[4] 謝守清.基于Simulink的“信號與系統”課程教學方法探索[J].寧波工程學院學報，2007，19（4）:100-102.

[5] 張猛，王曉峰.信號與系統建模與仿真[J].長春大學學報:自然科學版，2010，20（8）:63-65.

[6] 黨華麗.M atlab/Simulink仿真在信號與系統分析中的應用[J].信息技術，2010（3）:126-127.

[7] 李濤.Simulink仿真在《電路分析》課程教學中的應用[J].中國科教創新導刊，2010（2）:98-99.

[8] 李露，史振威，周付根.基于Matlab/Simulink的幅度調制與解調綜合實驗設計[J].實驗室研究與探索，2011，30（1）:96-99.