非線性系統神經網絡輸出穩定控制器的設計
歐陽林群, 王效華
(武夷學院電子工程系,福建武夷山 354300)
0 引 言
實際的非線性系統中存在時變性、不確定性等因素,使得傳統控制方法[1-3]難以實行有效的穩定性控制。系統運行過程的復雜性使得控制系統的控制面臨兩大主要難題:一個是難以用傳統的理論和方法對系統實時在線建模;另一個是難以用基于解析模型的解耦理論對其實施控制。已有很多學者[4-7]對非線性的控制作了研究。但是這些理論都基于一個前提:這就是必須寫出被控系統精確模型,而這一點在現實中幾乎不可能做到,尤其是對過程控制中系統隨著運行工況的不時改變、系統結構和參數不確定、非線性、滯后、諸多干擾等因素更是無法寫出其數學模型。
神經網絡具有良好的非線性逼近能力,可以克服控制器對被控系統精確數學模型的依賴,因此,在非線性系統的控制中得到了廣泛的應用。
在借鑒吸收前人研究的基礎上,文中將神經網絡引入到非線性系統的控制中,利用神經網絡具有逼近外界干擾信號[8-12]的能力,抵消系統所受擾動的影響,采用李雅普諾夫函數法給出了穩定性證明,并用仿真實驗驗證。
1 神經網絡算法分析
根據非線性系統穩定輸出設計的自適應反饋控制的要求,首先對所用神經網絡做數學分析。實際系統在運行過程中,不僅會受到系統內部的參數不確定性的影響,還會受到外部擾動的影響。神經網絡通過足夠的輸入信息和隱含層神經元數目,可以任意精度逼近連續非線性函數。因此,通過引入該網絡來補償系統所受到的外部干擾,實現基于神經網絡的輸出跟蹤控制,提高系統的魯棒性能。
1.1 神經網絡的逼近性
神經網絡的基本控制特性就是其任意精度的逼近性[13],設定 f(x)是映射Rn→Rm上的函數,那么在緊致集S∈Rn上的任一點x,隱層神經元權重和閾值的關系式:
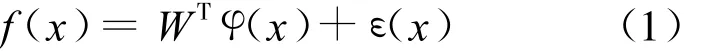
式中:x——輸入向量;
φ(?)——激活函數;
W——神經網絡輸出層的輸入矩陣;
ε(x)——近似誤差。
方程(1)表明,在任一緊致集合中,神經網絡能估測連續函數的狀態。實際上對一個正數εN,存在神經網絡參數滿足ε(x)≤εN(x∈S)。對于神經網絡,φ(x)滿足φ(x)=σ(VTx),其中V是首層的權值矩陣,σ(x)是S型函數。如果V是固定的,則神經網絡中唯一的設計參數就是W,則系統就變得更容易訓練。神經元隱層的數目越多,估測誤差ε(x)越小。對單層神經網絡函數,逼近誤差ε(x)是有界的。
1.2 非線性系統
為了分析和設計非線性控制器,設定多輸入單輸出(MISO)非線性系統用下面的式子描述:

式中:x——狀態向量;
u——輸入向量;
y——輸出向量。
2 神經網絡控制方案的設計
2.1 布魯諾標準型
精確線性化定理指出:設式(2)中h(x)存在m維函數,使得系統有相對階向量[r1,r2,…,rm],且系統總相對階r=r1+r2+…+rm=n(n為系統維數),即系統相對階等于系統維數,那么該系統就能實現精確線性化[14]。
設一個五階非線性系統,即式(2)中n=5。設輸出誤差為:

則跟蹤誤差的布魯諾標準型為:
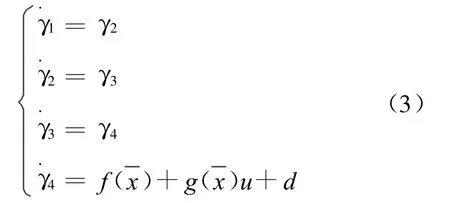
式中:u——系統的控制量;
d——有界干擾;
控制目標:如果系統滿足輸出反饋線性化的條件,運用文中提出的控制器,輸出量能穩定在一個平衡范圍之內。
2.2 相關假設
假設1:非線性系統(2)是輸入一狀態有界穩定的。
假設2:非線性系統(2)所有狀態可測。
2.3 神經網絡控制器的設計
定義濾波誤差σ如下:
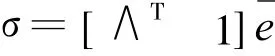
其中,∧=[λ1 λ2 λ3]T是系數變量,滿足當σ→0時,γ→0,其中s3+λ3s2+λ2s+λ1是Hurwitz多項式。
對上式求微分,并且把式(3)代入,則

根據反饋線性化理論,期望的希望輸入信號可以表達為:
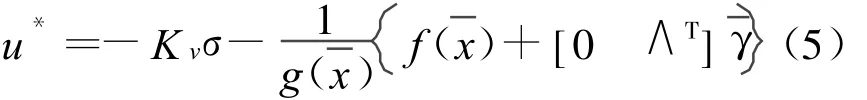
式中:Kv——常系數。

考慮到誤差信號,則上式變為:

把式(7)代入式(4)并整理,可以得到

其中:
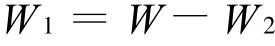
定義設定的控制信號:

如果umax為最大信號值,則系統的控制信號可以表示為:

2.4 含NN的控制系統框圖
含神經網絡的非線性控制系統框圖如圖1所示。

圖1 含神經網絡的非線性控制系統框圖
為了有效實現控制目的,控制圖采用雙環反饋,保證被控制非線性系統的穩定運行。內環為非線性NN的非線性控制,用來估測系統的動態運行,外環為PID跟蹤控制。
非線性系統結構框圖工作原理如下:
設d為系統未知干擾,權值誤差是ε,均是有界的。對于權值W滿足下式:
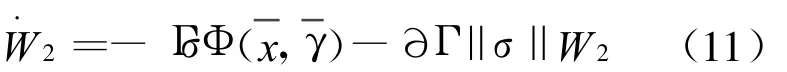
2.5 李雅普諾夫方法證明穩定性
李雅普諾夫函數方法的特點是不用求解系統的動態方程或分析參數特征根的實數部分正負特性,直接用確定并分析所研究狀態點處的廣義能量函數來判別系統的穩定性。將李雅普諾夫函數方法應用于神經網絡的穩定分析,可用來推導條件來保證權值的收斂。
運用選取V為李雅普諾夫函數,且V∈R,

計算導數得
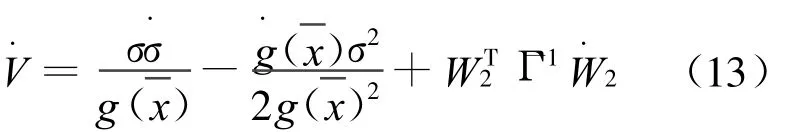

化簡后得到:
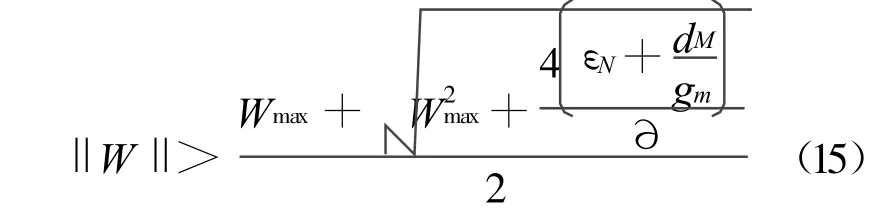
從上面分析可知,對于非線性系統的穩定,在用神經網絡優化系統時,神經網絡隱層的權值在(0,1)之間選擇,則需要滿足式(15)。
3 仿真與分析
3.1 仿真
為了驗證設計的基于李雅普諾夫的非線性神經網絡控制方法的控制效果,采用一個單機電力系統模型[15]作為仿真案例。神經網絡輸入層的權值取(0,1)之間的一個常數。
取參數分別為:

通過仿真,得到系統變化曲線如圖2所示。


圖2 系統變化曲線圖
3.2 結果分析
從仿真結果可以看出,文中提出的非線性控制器能夠很好地避免系統由于外界故障造成的不平衡,在經過振蕩后神經網絡非線性系統可以調節系統的運行狀態。
4 結 語
設計含有神經網絡的非線性系統的反饋穩定控制器,神經網絡算法具有朝最小誤差方向調整權值的內在因素,用李雅普諾夫函數方法對神經網絡算法收斂做分析,將設計的控制器運用于單機無窮大電力系統。仿真結果表明,提出的非線性控制器可以保證系統在受到外界擾動,平衡狀態被打破時對系統做有效的補償。
[1] 曹建福,韓崇昭,方洋旺.非線性系統理論及應用[M].西安:西安交通大學出版社,2001.
[2] 廖曉聽.穩定性的數學理論及應用[M].2版.武漢:華中師范大學出版社,2001.
[3] 李基成.同步發電機勵磁系統設計[M].北京:中國電力出版社,2002:8-20.
[4] 朱方,趙紅光,劉增煌,等.大區電網互聯對電力系統動態穩定性的影響[J].中國電機工程學報,2007,27(1):1-7.
[5] 陳利芳,陳天祿.淺談自并勵勵磁系統在大容量機組中的應用[J].繼電器,2007,35(1):81-84.
[6] 楊海龍,張天宇,郭驥俊.勵磁調節器中PSS對系統穩定性的作用及參數設置[J].華北電力技術,2005(12):12-14.
[7] 劉恩東,井元偉,王珂,等.基于神經網絡的非線性汽門控制器魯棒逆推設計[J].電力自動化設備,2005,25(10):13-16.
[8] 康錦萍,張粒子,徐英輝,等.基于神經網絡的快速汽門暫態穩定控制器的研究[J].電網技術,2003,27(11):22-25.
[9] HAN Yingduo,XIU Lincheng,WANG Zhonghong,et al.Artificial neural networks controlled fast valving in a power generation plant[J].IEEE Trans.Neural Networks,1997,8(2):373-389.
[10] Venayagamoorthy G K,Harly R G,Wunsch D C. Implementation of adaptive critic-based neurocontrollers for turbogenerators in a multimachine power system[J].IEEE Trans.Neural Networks,2003,14(5):1047-1064.
[11] 張騰,戴先中.汽門開度的神經網絡廣義逆系統控制[J].電力系統自動化,2000,24(17):25-27.
[12] 戴先中,張騰,張凱鋒,等.發電機勵磁與汽門系統解耦控制的神經網絡逆系統方法[J].中國電機工程學報,2002,22(11):75-80.
[13] Liu Lili.Guaranteed cost control of singular networked control systems with time-delay[C]// 2008CCDC.Yantai:Institute of Electrical and E-lectronics Engineers Computer Society,2008:415-418.
[14] 胡躍明.非線性控制系統理論與應用[M].北京:國防工業出版社,2002:110-121.
[15] KUNDER P.Power system stability and control [M].New York:McGraw-Hill Inc,1994.

