基于預測推理的蒸餾組分控制

李云鵬， 隋添翼， 張 洋， 劉 潤， 許紅巖， 于歡歡

（長春工業大學電氣與電子工程學院，吉林長春 130012）

0 引 言

當今化學工業生產過程日益依賴于儀表的準確測量和頻繁記錄，為滿足蒸餾組分的實時控制，推理控制理論日益凸顯其重要性。在從過程數據中提取有效信息時，推理控制系統能給出良好的解決方案。用最小二乘回歸法建立推理模型，從在線測量的過程變量中估計出產品組分的方法是簡單有效的。當考慮到過程數據的高度相關性，此方法卻未必可靠。

為了解決共線性問題，可采用偏最小二乘法設計組分估計器并建立產品組分固定的推理模型，Skogestad和Mejdell利用二進制精餾塔的線性模型將3種不同推理估計器進行對比后總結出:穩態推理估計器具有內在的前饋作用，良好的控制性能可以通過穩態主組分回歸推理估計器實現，這相當于使用了動態卡爾曼濾波器[1]。Kano等人進一步研究出了基于偏最小二乘法的推理模型，它能夠從在線測量的塔板溫度、流量、壓力等過程數據中估計出多組分精餾塔的產品構成。

為設計推理控制系統優化蒸餾組分控制的性能，需研究以下兩個問題:

1）推理模型的選擇;

2）控制結構的選擇。

解決重點放在推理模型的內在前饋作用上。提出一種基于推理模型的新型控制系統——預測推理控制系統。此方法通過控制將來的組分而非當前的組分，在擾動影響產品組分之前實現補償。

1 問題的定義

1.1 精餾塔的基本穩定情況

本次實驗的精餾塔由回流罐、再沸器和30個塔板等結構組成，塔的直徑為1 m。回流罐和再沸器的持液量分別為1.57 m3和3.14 m3。原料流在第15層塔板進入塔內，甲醇、乙醇、丙醇、丁醇的摩爾流量相等，總進料量為128 kmol/h。丙醇和乙醇在餾出物和塔底組分中關鍵組分的摩爾分數設定值皆為0.001 0。回流罐中的壓力由冷凝器控制，并假設其保持恒值1.013×105Pa。精餾塔內的蒸汽流量決定每個塔板處的壓力降，基本的穩態情況見表1。

表1 基本的穩定情況

用兩個溫度控制回路來保持產品組分達到其預設值，9層和22層塔板處的溫度作為被控變量，回流量和再沸器熱負荷作為相應的被控變量。通過反復實驗來調節溫控器的參數。餾出物和蒸余物的流量可分別控制回流罐和再沸器的延遲。仿真中假定塔板溫度、流量、壓力和液位等過程變量每一分鐘皆可測量。餾出物XD3中丙醇的摩爾分數和蒸余物XB2中乙醇的摩爾分數每10 min測定一次。

1.2 模型的模擬數據

為實現組分的緩慢變化，每個信號通過一階時滯模型過濾，加上這些隨機擾動，原料流量變化為±10%/（2 h）。從其穩態值分析，最大偏差將限制于±20%以內，全部仿真時間為20 h。在此情況下可以獲得有效的推理模型仿真數據。

改變設定值是閉環辨識的一種有效方法。當推理組分控制的應用取代溫度控制時，塔板溫度將會有很大的變動。因此，必須在溫度大幅度變化的情況下建立合理的推理模型，溫度的設定值需要隨辨識數據產生而改變，需嚴格控制設定值的大小，使產品的摩爾分數變化范圍不超出0～0.003。

1.3 控制系統性能的估計指標

推理模型的性能評估以解釋預測方差（EPV）為基礎，解釋預測方差可以從確認數據的模型應用中計算求得[2]:

式中:x——產品組分的測量值;

N——測量次數。

控制系統的性能由均方誤差（MSE）決定:

式中:xsp——x的設定值。

2 基于偏最小二乘法（PLS）的推理模型

在本次實驗中，PLS被用于從關聯過程變量中估計產品組分，產品組分的對數變換在這個實例中不會起到提高估計精度的作用，故在輸入變量和產品組分之間不使用非線性變換來處理非線性問題。此外，潛變量的數量取決于確認數據應用模型的結果[3]。PLS模型在單輸出情況下可寫作:

ui——第i次輸入變量;

vi——作為輸入的線性組合所給定的潛變量;

ai，bi——估測的回歸系數;

m——輸入變量個數;

r——潛變量個數，當輸入變量互相關聯時，r應當小于m。

2.1 穩態PLS模型

被估計的輸出變量是產品中丙醇和乙醇的摩爾分數（XD3，XB2），為了建立穩態PLS模型，需要通過改變進料量（F）和產品構成以生成99個不同的穩態數據[4]。全部30個塔板溫度和再沸器壓力作為輸入變量，潛變量的數量選為5個，此模型被稱為SS模型。

2.2 靜態/動態PLS模型

將5個塔板（第4，9，18，22，27）的溫度、回流量、再沸器熱負荷和壓力作為輸入變量。另外，當建立動態PLS模型時，要同時使用當前采樣時間的測量值與5，10，15 min時的測量值。由于被控變量即回流量和再沸器熱負荷不能立即影響產品的組分，因此，被控變量在當前采樣時間不可用作動態模型中的輸入變量[5]。研究下面4種模型:

靜態模型1:使用全部8個變量;

靜態模型2:使用5個塔板溫度和塔底處的壓力;

動態模型1:使用全部8個變量（總共30個輸入變量）;

動態模型2:使用5個塔板溫度和塔底處的壓力（總共24個輸入變量）。

2.3 預測推理模型

精餾塔中間溫度的變化要比塔底溫度的變化略顯快速，因此靜態估計器自身會略微存在前饋效應[6]。事實上，靜態模型2的估計值要高于測量值，如圖1所示。

圖1 產品組分的測量值與估計間的關系（靜態模型2）

當使用上述SS模型時，能得到相似的關系圖，如圖2所示。

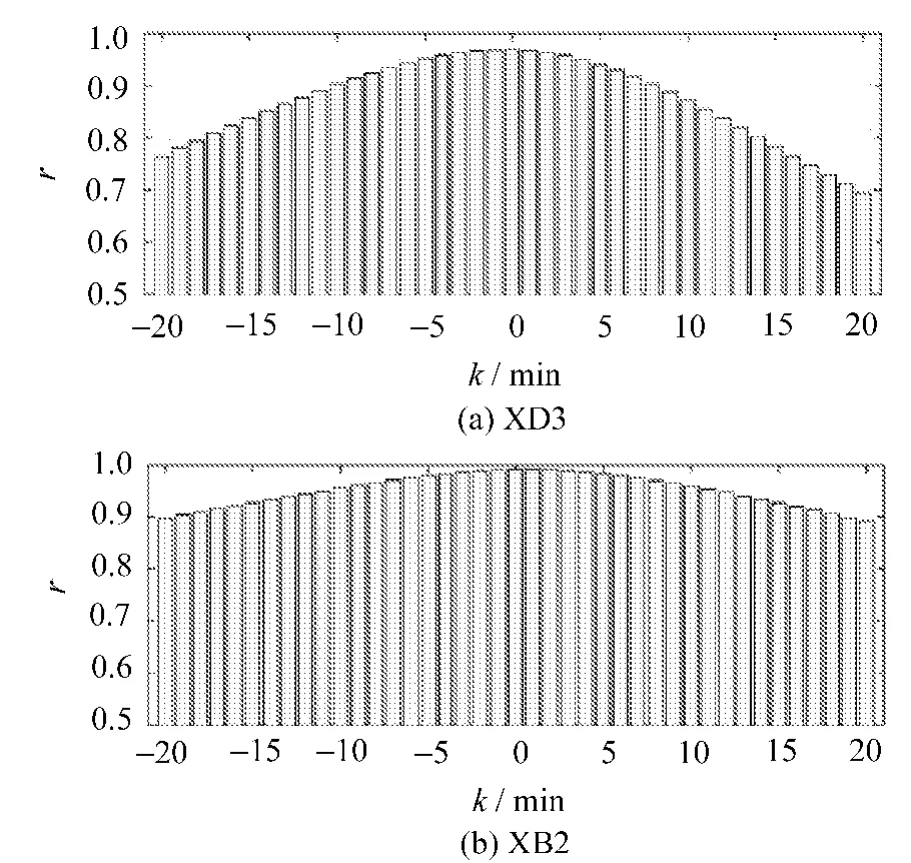
圖2 產品組分的測量值與估計間的關系（動態模型1）

圖中仍然顯示估計要高于測量值。當使用動態模型1時，測量值和估計之間沒有延遲，并且在最后的零點處高度的關系表明，動態模型1能夠很精確地估計產品組分。

3 推理控制

將上述推理模型用于產品組分控制。首先，研究推理模型的選擇，上文已介紹了用于控制塔底組分XB2的推理控制系統，而塔頂溫度控制系統保持不變。控制結果如圖3所示。

圖3 塔頂、塔底產品組分控制結果

3.1 傳統的推理控制

上述推理控制系統通過控制回流量和再沸器熱負荷來控制XD3和XB2的估計。為此，要用到多回路比例積分控制[7]。

為改善推理控制系統性能，使其與在溫度控制方面發揮的作用相當，需要使用時序數據建立并使用更新的推理控制模型。在這個例子中，使用兩次迭代即可。但迭代模型會消耗時間和精力，這樣的推理控制尚不可稱其先進。

3.2 預測推理控制

在不同預測時間（α=5，10，15 min）下建立預測推理模型和傳統的推理模型（α=0 min），并將二者比較，仿真結果見表2。

表2 預測推理控制與傳統推理控制在使用靜/動態模型時的對比

在所有情況下均使用相同的控制參數來抑制調諧效應。

表2顯示，當α預測時間增加時，估計精確度降低。動態控制模型1的估計精確度明顯高于靜態控制模型2。動態模型1和靜態模型2的預測推理控制系統的控制性能也并非差異迥然。由此可見，使用最精確的推理模型未必會達到最好的控制性能[8]。然而，預測推理控制的控制性能要比表2中的溫度控制的控制性能差一些。

為提高估計精度和控制性能，使用迭代模型技術，仿真結果見表3。

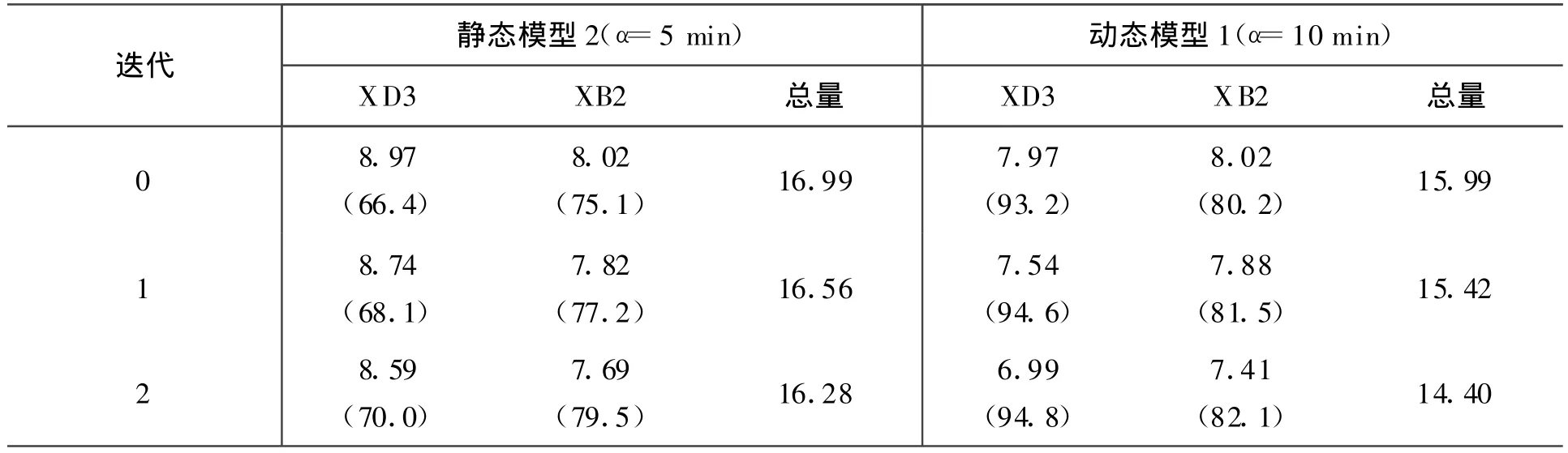
表3 預測推力控制系統使用靜/動態模型的比較

由此可見，使用動態模型1的預測推理控制的優勢。在兩次迭代之后，動態模型1的預測推理控制性能被進一步完善，并明顯優于它在溫度控制時的表現。

上述預測推理控制與模型預測控制有本質上的區別，模型預測控制的動態過程模型需要能夠描述被控變量對控制變量的影響，而預測推理控制不需要這樣的動態模型[9]。事實上，在推理模型中，任何被測變量都可以作為輸入變量。并且推理模型可以是靜態的，而動態模型具有很高的估計精度。

4 結 語

通過幾個推理控制系統的比較可以看出，盡管從控制精度的角度看動態模型要優于靜態模型，但動態模型無法始終令系統持獲得良好的控制性能。由于自身的前饋效應，靜態模型也體現了很好的控制效果。

為了在擾動對產品組分產生影響之前將其檢測出來，提出了以預測組分為控制變量的推理模型，建立了預測推理控制系統[10]。實踐證明了迭代模型和預測推理控制模型在控制系統性能方面各自的優勢。因此，預測推理控制方法在蒸餾過程產品組分控制中將日益體現其重要價值。

[1] 黃德先，王京春，金以慧.過程控制系統[M].北京:清華大學出版社，2011:120-125.

[2] 金以慧.過程控制[M].北京:清華大學出版社，1993:287-310.

[3] 陳優先.化工測量及基表[M].北京:化學工業出版社，2010:26-75.

[4] 徐喆，柴天佑，王偉.推理控制綜述[J].信息與控制，1998，27（3）:206-305.

[5] 嚴愛軍，張亞庭，高學金.過程控制系統[M].北京:北京工業大學出版社，2010:150-156.

[6] 俞金壽.工業過程先進控制技術[M].上海:華東理工大學出版社，2008:65-76.

[7] Chen C Y，SUN C C.Adaptive inferential control of packed-bed reactors[J].Chem.Eng.Sci.，1991，46（4）:1041-1054.

[8] 王驥程.化工過程控制工程[M].北京:化學工業出版社，1991:190-199.

[9] Shinskey F G.過程控制系統[M].北京:清華大學出版社，2004:277-293.

[10] 王樅，李睿凡.控制系統理論及應用[M].北京:北京郵電大學出版社，2009:29-56.