基于二次B樣條的廣義差分法

秦丹丹， 馮 雪， 左 平

（空軍航空大學基礎部，吉林長春 130022）

0 引 言

廣義差分法從微分方程的積分守恒形式出發，通過選取試探函數空間為有限元子空間，檢驗函數空間為相應于對偶剖分的分段低次多項式函數空間來導出計算格式。文中介紹了基于二次B樣條的廣義差分法。B樣條函數具有很多優良性質，如:有明確的表達式，具有有限支集、對稱性和良好的光滑性等。因此，B樣條函數作為試探函數空間的基函數可以保證系數矩陣的對稱性、正定型和稀疏性。二次B樣條廣義差分法既保持了差分法的簡單性，又兼具有限元的精確性。

1 B樣條函數

m階B樣條函數Sm（x）[1]定義如下:

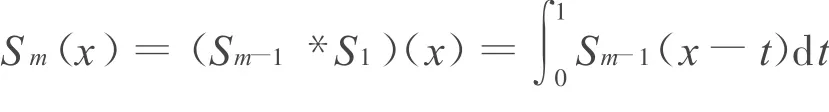
其中S1（x）為[0，1]上的特征函數。值得注意的是B樣條函數的卷積定義式有下面的等價形式[2]:

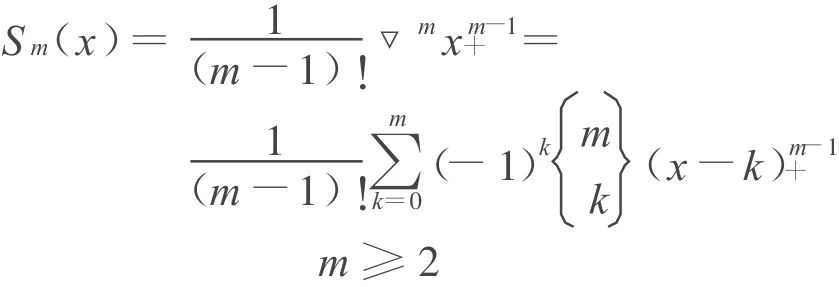
由以上定義式可以得到三階二次B樣條函數的表達式:

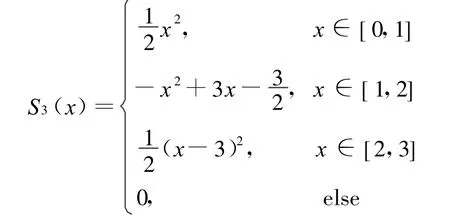
顯然，m階B樣條是分段m-1次多項式，且具有緊支集suppSm（x）=[0，m];此外，m階B樣條還具有如下性質:

1）Sm（x）是以 x=為對稱軸的單峰值山丘狀函數;

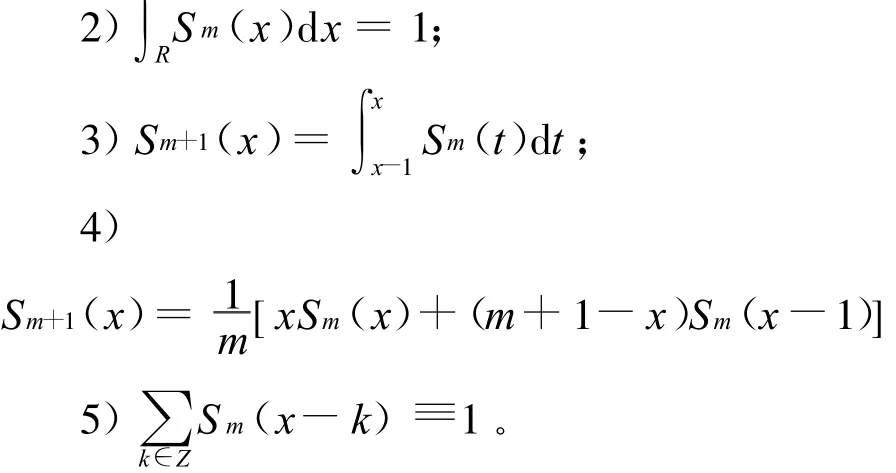
B樣條性質的證明詳見文獻[2-3]。

2 基于B樣條的廣義差分法

考慮二階常微分方程:

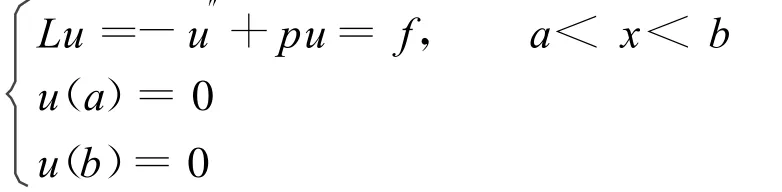
其中，p∈C（I），p≥0，f∈C（I），I=[a，b]。

對區間[a，b]進行均勻剖分，網格節點為a= x0＜x1＜…＜xn=b，且在區間[a，b]外分別擴充兩點:x-2，x-1和 xn+1，xn+2，相鄰節點間的距離記為h，記Ii=[xi-1，xi]。

構造基函數

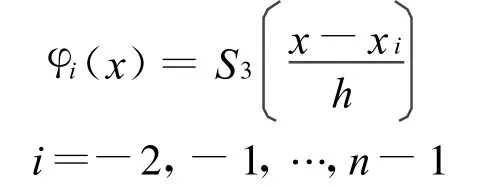
則函數組{φi（x）}為區間[a，b]上以{xi}為節點的二次樣條的一組基。

為方便處理邊值條件，將前兩個函數換成線性組合[4]:2φ-2（x），φ-1（x）-φ-2（x）。同時將最后兩個基函數換成:φn-2（x）-φn-1（x），2φn-1（x）。變換前后基函數對應的函數空間是等價的。改換后的基函數稱為變形的二次B樣條基函數，仍記為{φi（x）}。在左端點處滿足φ-2（x0）=1，φi（x0）=0（i≠-2），在右端點處滿足φn-1（xn）=1，φi（xn）=0（i≠n-1）。

試探函數空間Uh取為滿足邊值條件的二次B樣條有限元空間。由于文中考慮的是零邊值問題，所以任一uh∈Uh可以表示成

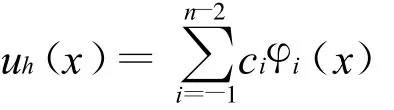
式中:ci——待定系數;

uh——自由度為n，故試探函數空間的維數為n。

對偶剖分取為a=x0＜x1＜…＜xn=b，即對偶剖分與原剖分相同。檢驗函數空間Vh取為相應于對偶剖分的分段常數函數空間。檢驗函數為:

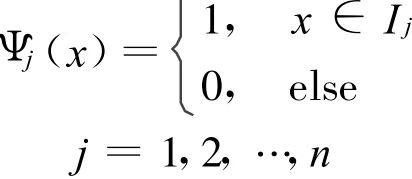
可見，檢驗函數空間與試探函數空間維數相同。

因此，基于二次B樣條的廣義差分格式[5]為:求uh∈Uh，使得

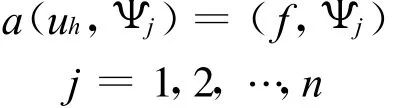
進一步應用分部積分公式，結合邊值條件就得到微分方程的積分守恒形式如下[6]，求uh∈Uh，使得

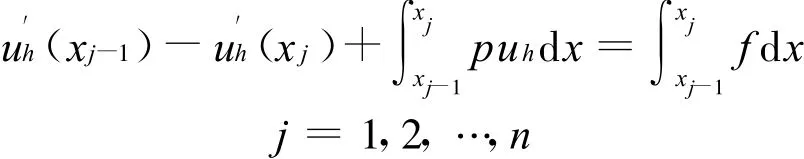
在網格節點處取值非零的導數有:

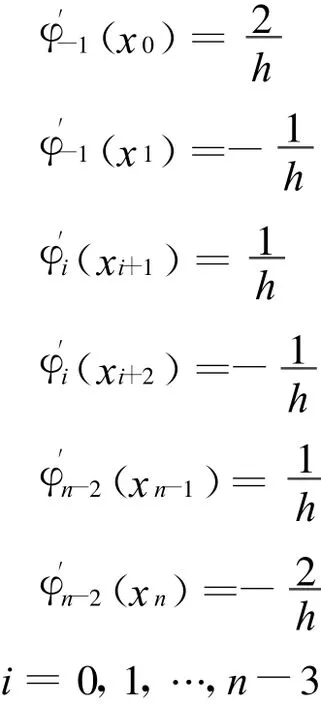
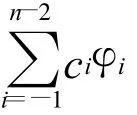
通過研究學習，我們發現二次B樣條廣義差分法有以下誤差估計[5，7-8]:

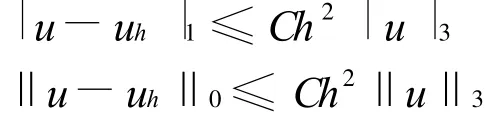
可以看出，二次B樣條廣義差分法不具有最佳L2收斂階。

3 數值算例

在已知二階常微分方程中，令a=0，b=1，p =0，f（x）=4π2sin（2πx）。此問題的精確解為u（x）=sin（2πx）。用uh（x）表示數值解，定義數值解在H1半模和L2模下的誤差:

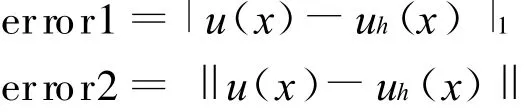
誤差error1對應的收斂階記為order1，誤差error2對應的收斂階記為order2。用n表示求解區間的剖分數。應用數學軟件Matlab，得到誤差與收斂階數據見表1。

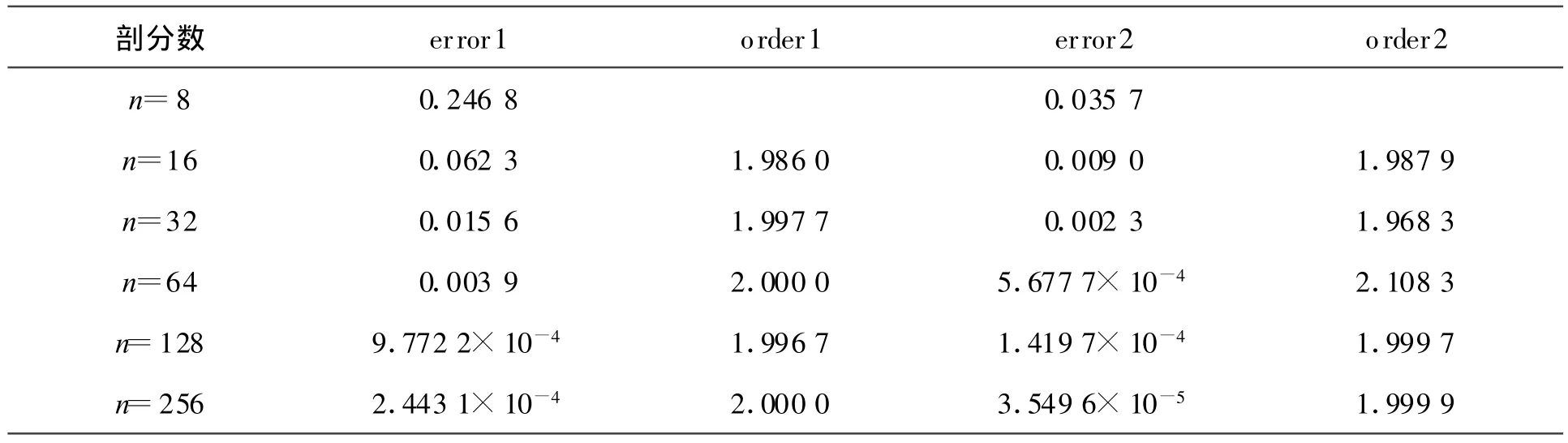
表1 誤差與收斂階

表中數據說明:隨著網格剖分的加密，數值解與精確解越來越接近。在H1半模和L2模下，二次B樣條廣義差分法均具有二階收斂精度。

4 結 語

當試探函數空間為Lagrange型二次元時，相應于節點和半整節點存在兩組不同的基函數，而二次B樣條有限元空間只有相應于節點的一組基函數，因此，兩種方法的系數矩陣階數之比約為2∶1。此外，B樣條有限元可以保證位函數的光滑性。但是，二次B樣條廣義差分法不具有最佳L2收斂階，這個缺點在一次和三次B樣條廣義差分法中可以得到避免。因此，在廣義差分法中，關于試探函數空間的選取仍然是至關重要的。

[1] 陳廣生.B樣條函數的一個性質[J].廣西科學，2008，15（4）:381-382.

[2] 梁學章，李強.多元逼近[M].北京:國防工業出版社，2005.

[3] 孫家昶.樣條函數與計算幾何[M].北京:科學出版社，1982.

[4] 梁旭彪，簡柏敦，倪正光.B樣條有限元法[J].中國電機工程學報，1987，7（6）:9-20.

[5] LI Rong-hua，CHEN Zhong-ying，WU Wei.Generalized difference methods for differential equations [M].New York:Marcel Dekker Inc.，2000.

[6] 高廣花，王同科.兩點邊值問題基于三次樣條插值的高精度有限體積元方法[J].山東大學學報，2009，44（2）:45-51.

[7] CHEN Zhong-ying.Error estimates for generalized difference method[J].Acta Sci Natur Univ Sunyatseni，1994，33（4）:22-28.

[8] CHEN Zhong-ying，LI Rong-hua，ZHOU Ai-hui. A note on the optimal-estimate of the finite volume element method[J].Advances in Computational M athematics，2002，16（4）:291-303.