托柱轉換結構的彈性抗震性能研究
呂劍勇
(廣東科貿職業學院環境藝術系,廣東廣州 510430)
0 引 言
隨著建筑功能的日趨復雜,高層建筑中設置轉換層的情況已是非常普遍。現階段轉換構件的類型有梁、桁架、斜柱、拱、厚板等,其中,桁架又包括斜桿桁架和空腹桁架等形式。在上述幾種轉換構件當中,轉換梁的截面往往很大,而桁架的上下弦桿可以分別設置在上下樓層,不占空間,便于轉換層的使用,并且桁架的外形輕巧,能提高建筑的藝術性。此外,空腹桁架由于不設斜腹桿,有利于建筑門窗的布置,所以空腹桁架是一種非常理想的轉換構件形式。
帶轉換層高層建筑是一類復雜高層建筑結構,由于抗側力結構沿豎向不連續,不可避免地帶來結構剛度和應力沿豎向的突變而形成結構薄弱層,導致其在地震作用下的傳力機理十分復雜[1-8]。采用何種轉換形式更有利于抗震,是科研技術人員必須面對和解決的問題。就轉換構件本身而言,采用空腹桁架轉換不但更能滿足建筑功能要求,而且在靜力性能上也具有一些優點,特別是對于托柱轉換結構,空腹桁架轉換比梁式轉換具有更好的靜力性能[9-10]。
為進一步研究空腹桁架轉換結構在托柱時的抗震性能,文中以某托柱轉換結構為計算模型,分析當采用空腹桁架轉換時的基本動力特性和彈性動力時程響應,并與相同條件下的梁式轉換結果相比較,以判別在托柱時采用空腹桁架轉換的抗震可行性。
1 建立計算模型
采用結構分析程序SAP2000作為理論計算手段,建立三維空間有限元計算模型,如圖1所示。
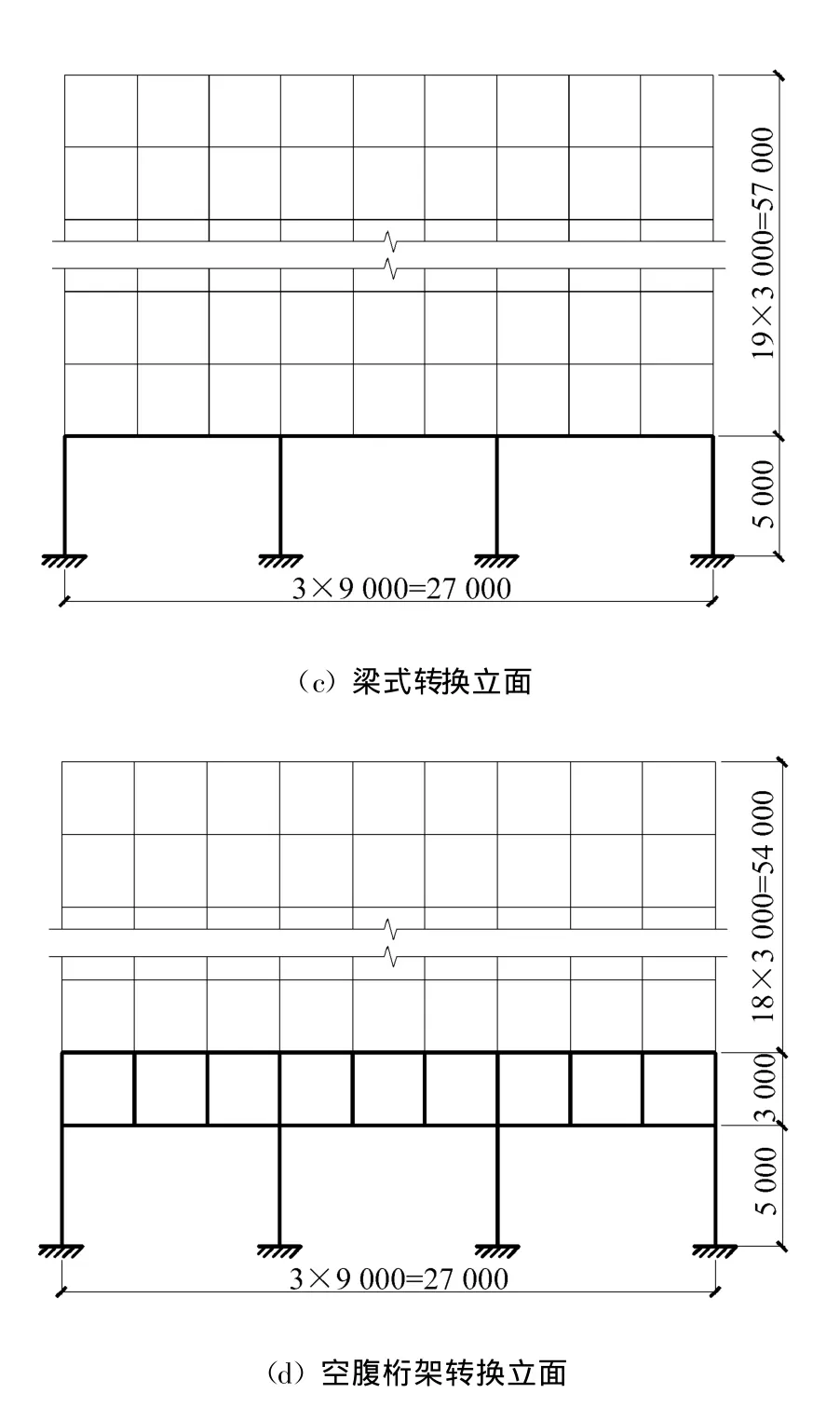
圖1 某托柱轉換結構計算模型
除轉換構件分別采用轉換梁和轉換空腹桁架外,其余結構構件以及結構布置均相同。計算模型中的主要構件截面尺寸見表1。
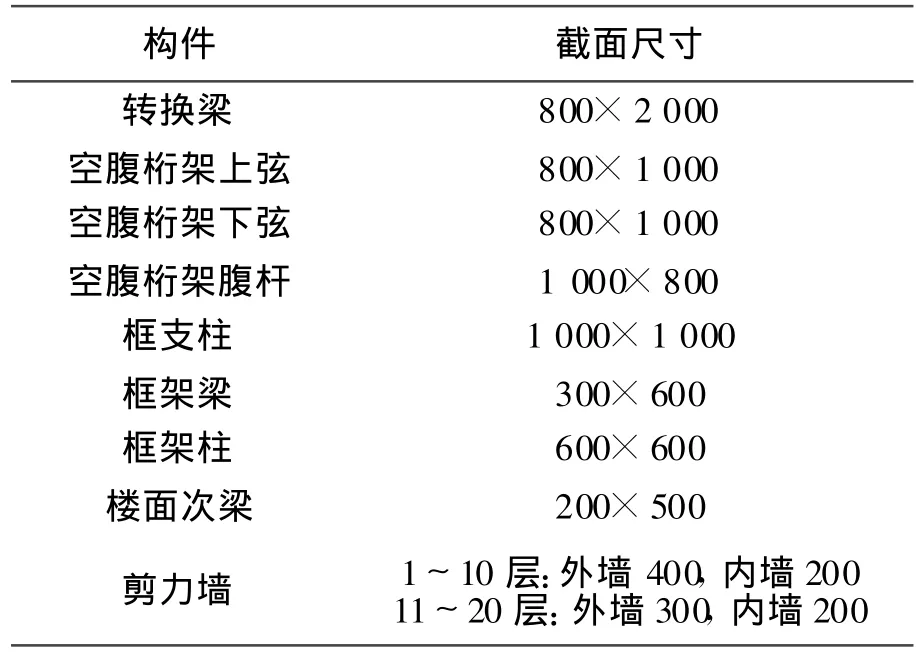
表1 主要構件截面尺寸 mm
在SAP2000有限元模型中,梁、柱和空腹桁架桿件采用兩節點空間框架單元,每節點有6個自由度;剪力墻和樓板采用空間4節點板殼單元,每節點有6個自由度,能夠順利地與空間框架單元協調[11]。
2 基本動力特性分析
文中計算了兩種轉換結構的前30個自振周期和振型,其中前三階平動周期和前二階扭轉周期及相應的振型質量參與系數見表2。
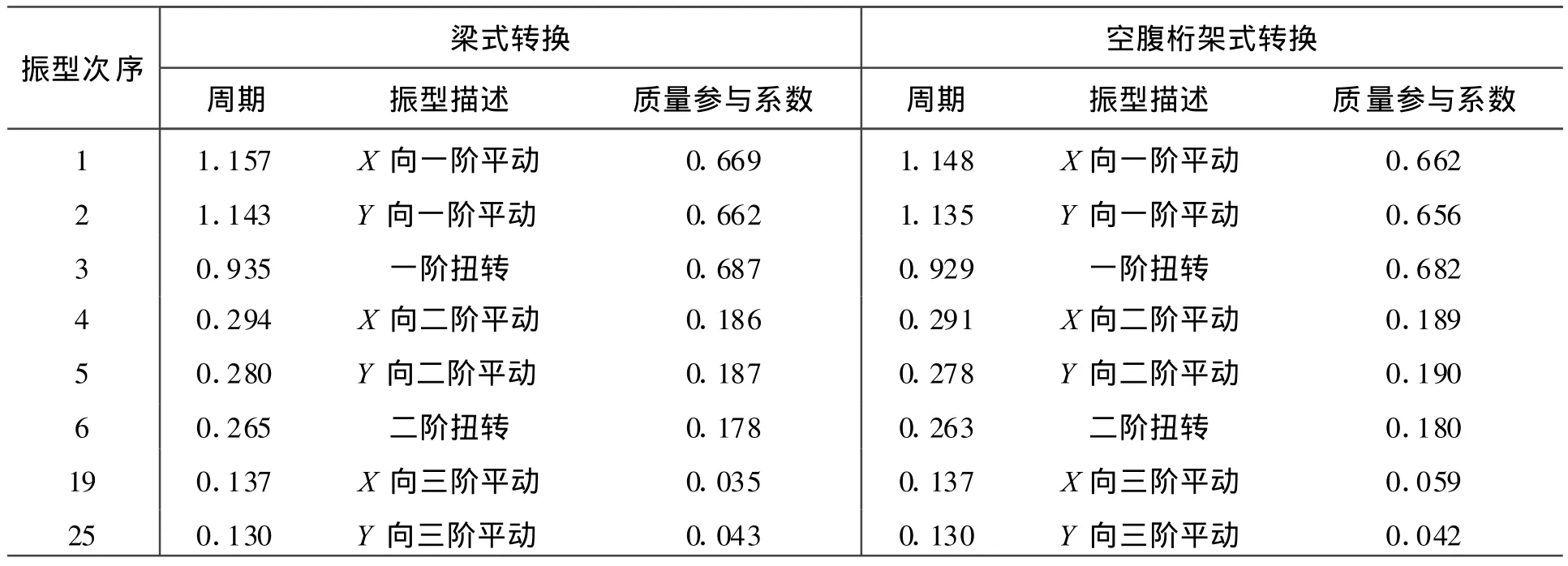
表2 計算模型的自振周期 s
計算模型的一階振型如圖2和圖3所示。
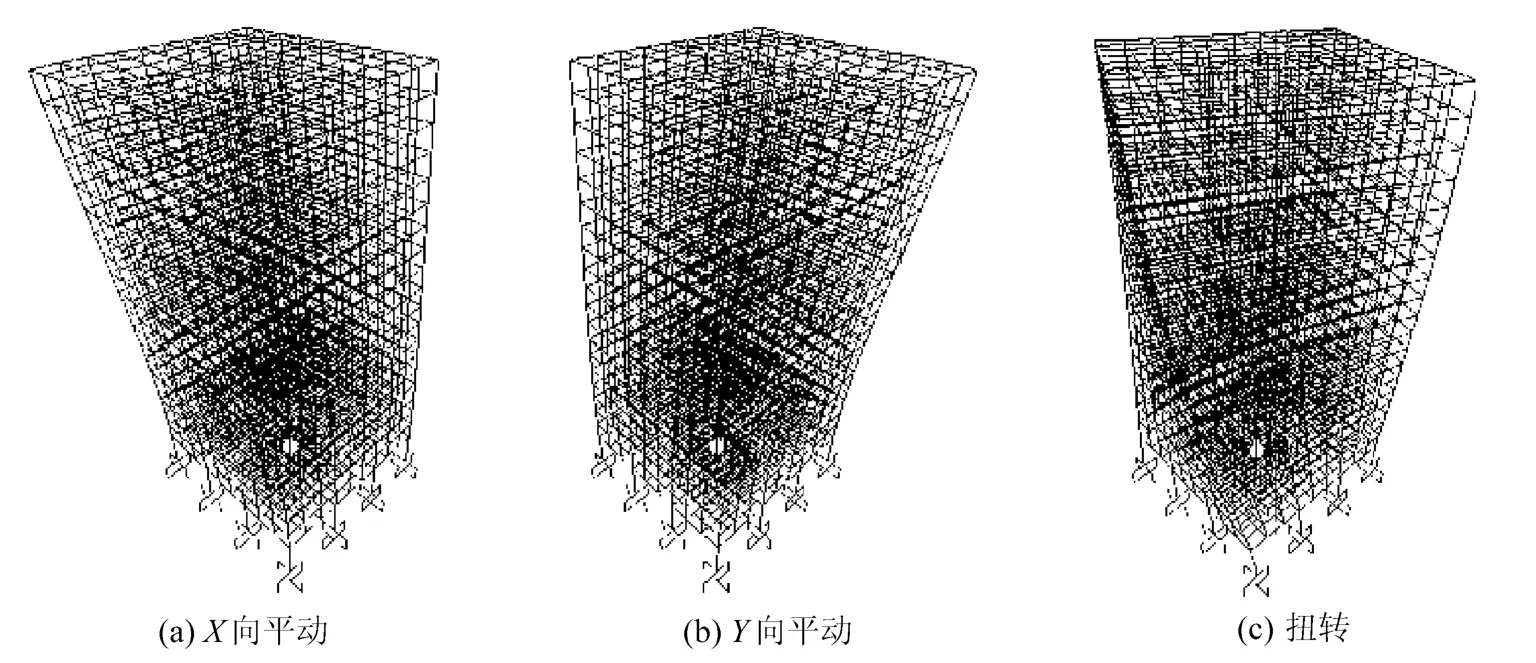
圖2 梁式轉換一階振型圖
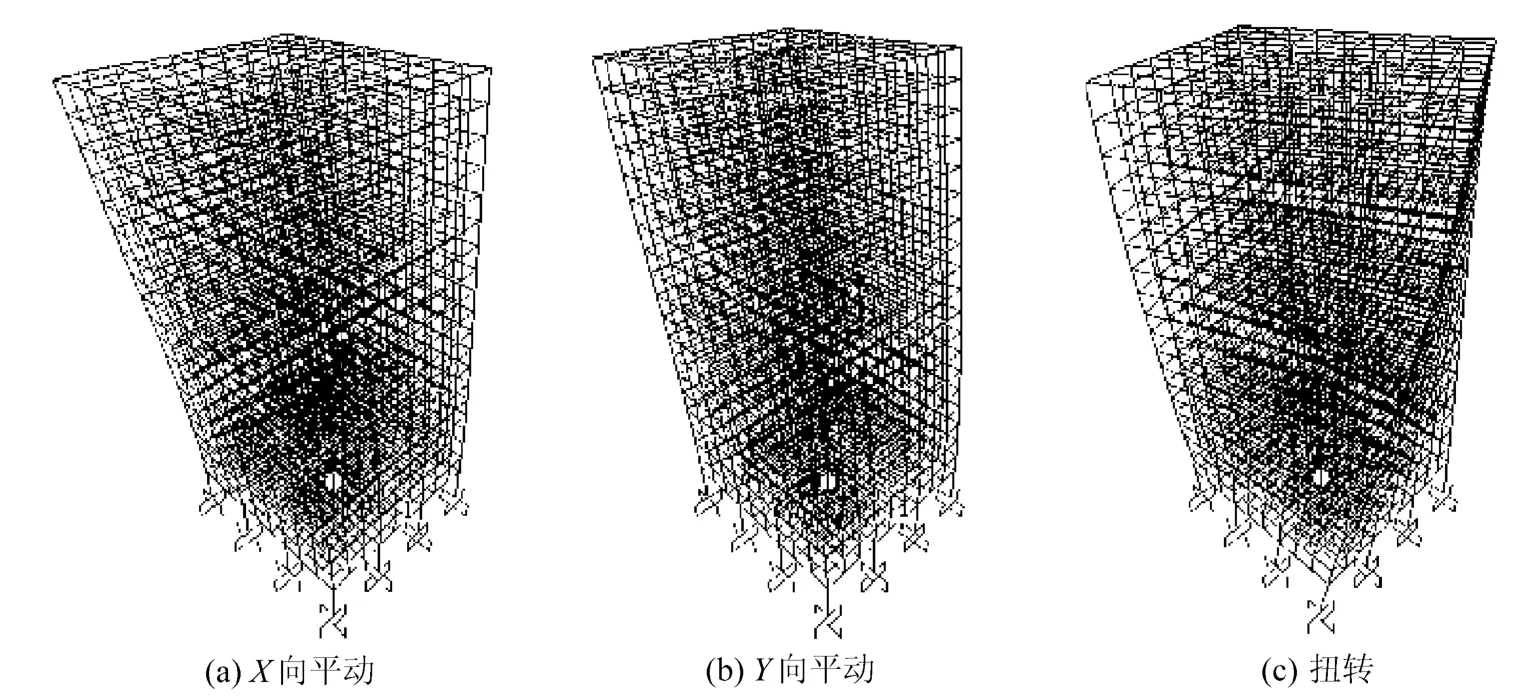
圖3 空腹桁架式轉換一階振型圖
分析自振周期的計算結果,空腹桁架轉換結構的前30個自振周期與梁式轉換結構非常接近,僅低階振型的自振周期略有差別,但相差僅為0.78%,而高階振型的自振周期則完全相同。兩種轉換結構的振動形式和振型出現次序也非常一致,X方向前三階平動振型分別出現在第1,4,19振型,Y方向前三階平動振型分別出現在第2,5,25振型,前二階扭轉振型分別出現在第3,6振型。從振型質量參與系數來判別,兩種轉換結構均是以一階振型為主。由此可見,在托柱時,空腹桁架轉換結構與梁式轉換結構的動力特性是非常相近的。
3 彈性動力時程分析
文中按照7度多遇地震來計算兩種轉換結構的動力時程響應,分別輸入EL-Centro地震波-南北分量和唐山地震波-南北分量(北京飯店觀測點),地震加速度時程曲線的最大值取35 gal,調整后的加速度時程曲線如圖4所示。
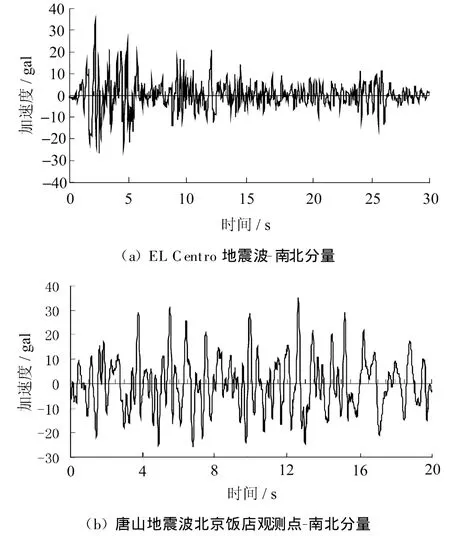
圖4 調整后的加速度時程曲線
為簡化工作,文中僅對兩種轉換結構的X方向作彈性時程分析。
計算模型在X方向的樓層剪力包絡圖如圖5所示。
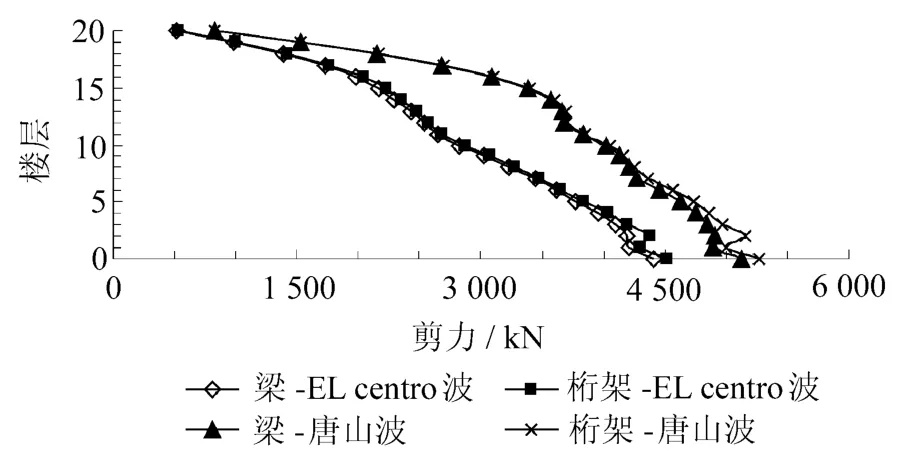
圖5 計算模型在X方向的樓層剪力包絡圖
由圖5可見,兩種轉換結構的剪力在底部幾層略有不同,空腹桁架式轉換結構在兩條地震波作用下的剪力均略大于梁式轉換結構,并且在轉換層位置存在微小的剪力突變現象;在結構的中部和上部,兩種轉換結構的剪力分布基本相同。說明采用不同的轉換構件對轉換層附近的上下幾層樓層剪力有所影響,但影響不大。此外,兩種轉換結構由唐山波引起的樓層剪力均大于EL-Centro波引起的樓層剪力。
計算模型在X方向的樓層側移包絡圖如圖6所示。
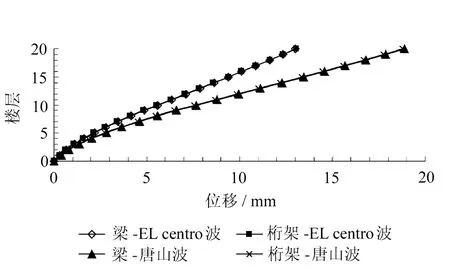
圖6 計算模型在X方向的樓層側移包絡圖
計算模型在X方向的層間位移角包絡圖如圖7所示。
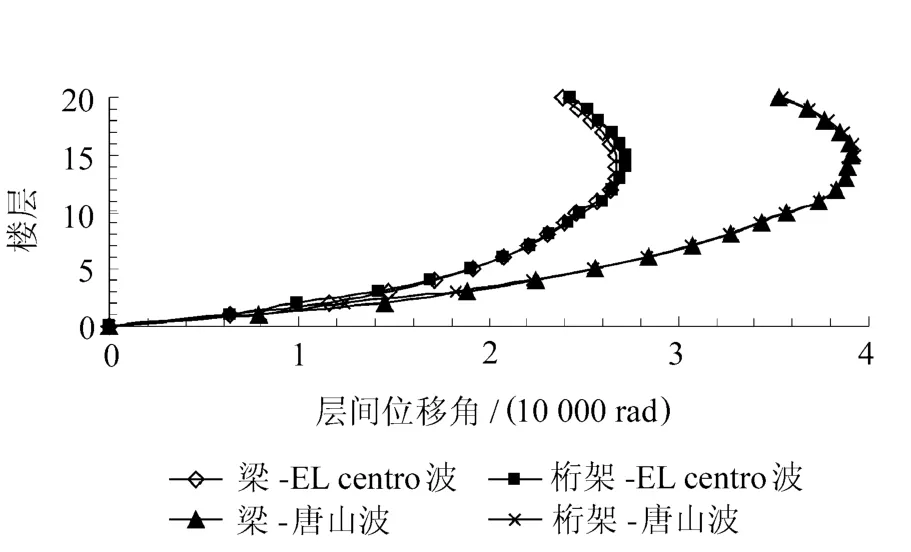
圖7 計算模型在X方向的層間位移角包絡圖
由圖6和圖7可見,兩種轉換結構在兩條地震波作用下的側移包絡曲線和層間位移角包絡曲線均很接近,可以判別兩種轉換結構的整體抗側剛度非常接近。在結構的下部幾層,梁式轉換結構的層間位移角略大于空腹桁架式轉換結構,而在結構的上部幾層,則情況相反。兩種轉換結構的最大層間位移角均出現在結構高度的3/4處。
4 結 語
1)從自振周期和振型的計算結果可知,空腹桁架轉換結構與梁式轉換結構的基本動力特性是非常相近的,兩者的低階振型自振周期存在微小差別,而高階振型自振周期則完全相同,兩者的振動形式和振型出現次序也完全一致。
2)從動力時程響應的計算結果可知,在轉換層附近的幾層,兩種轉換結構的樓層剪力略有差別,但差別不大。在地震波作用下,兩者的樓層側移和層間位移角基本相同,說明兩者的整體抗側剛度相當。
通過上述分析可以得出結論,在托柱情況下,采用空腹桁架轉換與采用梁式轉換在彈性階段具有相近的抗震性能,采用空腹桁架作為轉換構件在抗震上是完全可行的。
[1] 徐培福,王翠坤,郝銳坤,等.轉換層設置高度對框支剪力墻結構抗震性能的影響[J].建筑結構,2000,30(1):38-42,29.
[2] 王森,魏璉.不同高位轉換層對高層建筑動力特性和地震作用影響的研究[J].建筑結構,2002,32(8): 54-58.
[3] 趙西安.高層鋼筋混凝土建筑結構抗震設計的一些建議[J].建筑結構,1994(4):3-10.
[4] 姜華,魏群,焦濤,等.梁腹板開圓孔鋼框架的抗震性能分析[J].河南理工大學學報,2008,27(3):333-338.
[5] 劉伯棟,高大峰,張靜娟.中承式鋼筋混凝土拱橋結構動力特性研究[J].河南理工大學學報,2009,28(2):175-179.
[6] 龔耀清,馬伏龍.超高層建筑巨形框架與其基礎地基共同工作的簡化分析[J].河南理工大學學報,2006,25(2):145-150,161.
[7] 龔耀清,楊博.超高層建筑空間巨形框架的半解析自由振動分析[J].河南理工大學學報,2005,24(1): 65-68,73.
[8] 龔耀清,吳華芹,甄靜水.超高層建筑空間巨形框架的地基、基礎、上部結構共同工作的簡化振動分析[J].河南理工大學學報,2007,26(3):322-328.
[9] 呂劍勇.高層建筑梁式與空腹桁架式轉換結構的比較研究[D]:[碩士學位論文].廣州:華南理工大學,2007:7-25.
[10] 呂劍勇.空腹桁架轉換結構的靜力性能研究[J].建筑科學,2010,26(3):62-65.
[11] 彭俊生,羅永坤.結構概念分析與SAP2000應用[M].成都:西南交通大學出版社,2005:1-67.

