個體風險模型中總索賠額分布函數的估值問題
趙麗霞
(山西大學商務學院,山西太原 030031)
0 引 言


的基礎上,對S的分布函數FS(x)的取值范圍進行了探討。
1 主要結果
引理1 若Xi(i=1,2,…,n)相互獨立,服從參數為λ的指數分布,則X1+X2+…+Xn服從參數為(n,λ)的Γ分布,其分布函數為:

證明
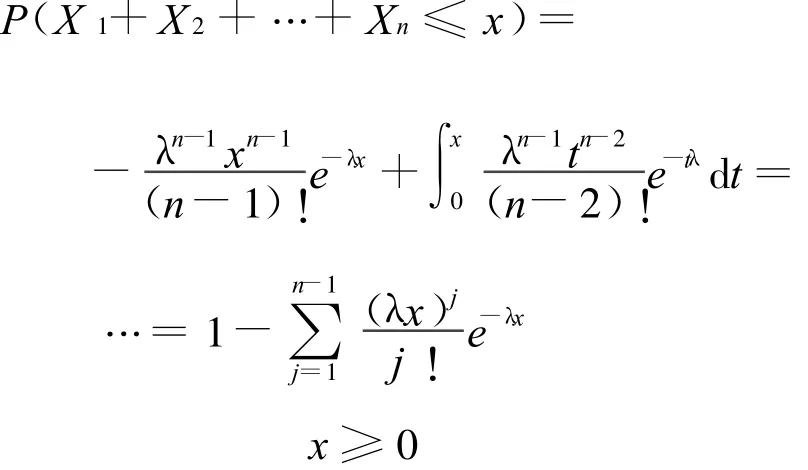

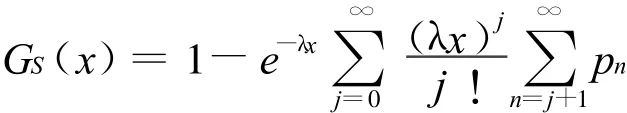
證明


引理3[7]若對于任意的x(x≥0),有

即F(x)為NBUE(NWUE)類分布,則對于任意的x(x≥0),有
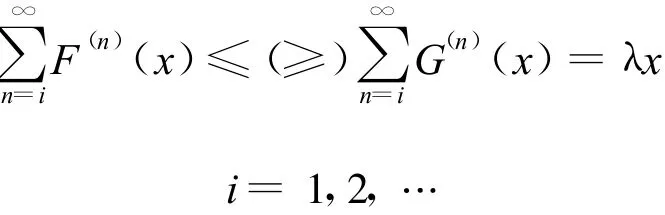
G(x)——指數分布函數,其參數為λ。
首先,作為文獻[3-6]的推廣,我們研究個體理賠額服從指數分布下總理賠額概率密度的確定問題。


證明 由引理1和引理2易知
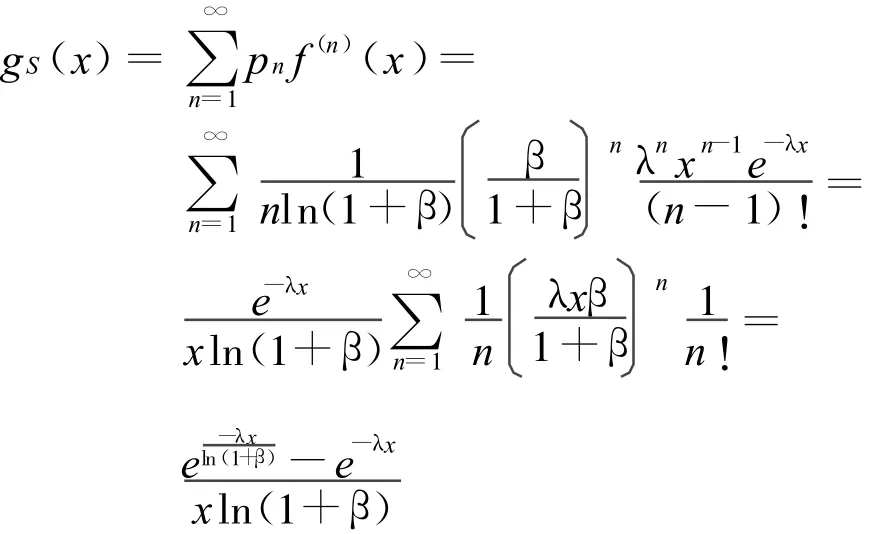
下面在Xi的分布函數為抽象函數F(x)的基礎上,討論總理賠額的分布函數的估值問題。


證明 由卷積公式及數學歸納法易知

因此

另一方面

定理3 若對于任意的x(x≥0),有

即F(x)為NBUE類分布,N服從參數為β的Logarithmic分布,則對任意的x(x≥0),有

其中

證明 易知Logarithmic分布的分布律組成的數列{pn}是單調遞減數列,即

由引理3,可得

另一方面,由引理2和引理3,得

另由文獻[8]可知:

定理4 若對于任意的x(x≥0),有
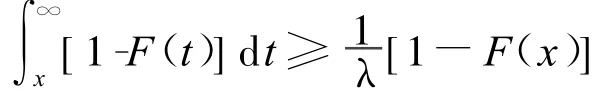
即F(x)為NWUE類分布,N服從參數為β的Logarithmic分布,則對于任意的x(x≥0),有

其中


2 結 語
保險系統中,總索賠額的分布函數是保險費率厘定的基礎,因此對其進行研究是完全有必要的。但是,通常情況下總索賠額分布函數的精確表達式是很難得到的。文中在一些基本假定下,探討了總索賠額分布函數的估值問題,推導出了它的上、下界,為費率厘定提供了基礎。當參保人數為一般的計數過程時,總索賠額分布函數的估值是要進一步研究的內容。
[1] 楊靜平.非壽險精算學[M].北京:北京大學出版社,2006.
[2] Cai J,David C,Dickson M.Upper bounds for ultimate ruin probabilities in the sparre andersen model with interest[J].Insurance:Mathematics and Economics,2003,32:61-71.
[3] 王志忠,劉裔宏.保險系統的損失分布模型[J].經濟數學,1997(2):55-58.
[4] 吳和成.保險系統的一個損失分布模型[J].系統工程,2003,21(1):94-97.
[5] 劉維奇,史金鳳.保險系統的兩類損失分布模型[J].山西大學學報:自然科學版,2005,28(3):247-252.
[6] 李東梅,劉維奇.保險系統損失分布模型新探[J].系統工程,2004,22(2):20-22.
[7] Barlow R E,Proschan F.Statistical theory of reliability and life testing[M].New York:Holt,1975.
[8] Ross S M.Stochastic process[M].New York: John Wiley&Sons,1983.

