具有生物控制的非自治n種群競爭系統的全局吸引性
李玉輝
(北方工業學校數學教研室,遼寧盤錦 124021)
0 引 言
具有重要實際意義的多種群生態系統動力學性質歷來受到學術界的重視,現已取得了大量的研究成果[1-5]。在具體的生態問題中,人們為了達到對生態系統的控制,采用了一種有效的辦法即是引入反饋控制變量。對于下述反饋控制系統:

式中:n(t)——t時刻種群的密度;
u(t)——t時刻反饋控制變量。
文獻[6-7]研究了該模型正平衡點的穩定性,給出了全局漸近穩定的充分條件。基于以上工作,文中考慮如下具有生物控制的非自治n種群Lotka-Volterra競爭系統:
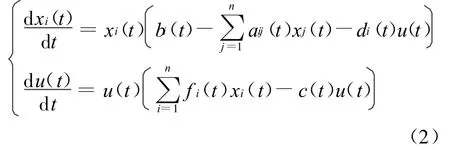
式中:xi(t) ——第i個相互競爭種群(即食餌種群)在時刻t的密度,i=1,2,…,n;
u(t)——控制變量(即捕食者種群)在時刻t的密度;
aij(t),bi(t),ci(t),di(t),fi(t)(i,j=1,2,…,n)——皆為關于t∈R+=[0,∞)的連續且恒正有界函數。
系統(2)的生態意義是:當n個相互競爭種群的增長率較高時,引入一個捕食者種群實施生物控制,借以實現對系統的整體控制,使人們能夠在生態平衡中獲益。由于生物控制代表人類的干擾作用,所以研究生態系統(2)的動力學性質更有實際應用價值。
設
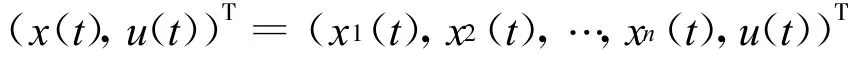
是系統(2)的任意解,初始條件為:
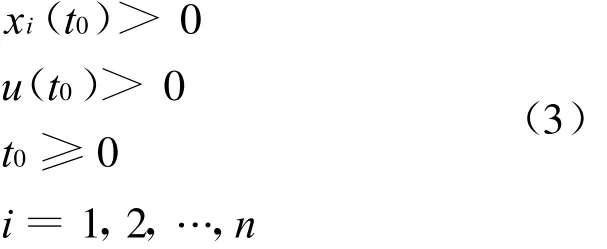
文中記:
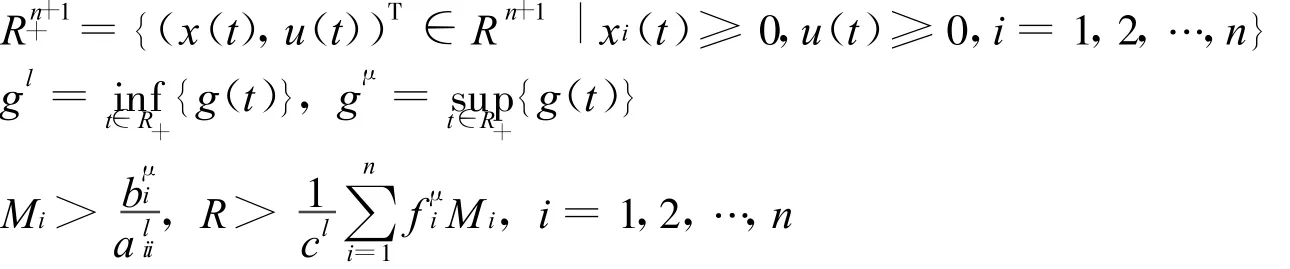
式中:g(t)——連續有界函數。
近年來,具有生物控制的生態系統備受關注[8-9]。據悉,至今尚未有學者研究系統(2)滿足正初值條件(3)的動力學性質。文中首先運用微分方程中比較原理研究系統的一致持久性,然后通過構造Lyapunov函數得到系統全局漸近穩定的充分條件,最后應用文中定理對實例的動力學行為進行了判定。
1 持久性
定義1 如果存在一個緊區域D?Rn+1+,使得系統(2)滿足正初值條件(3)的每一解最終進入并保留在區域D,則稱系統(2)是一致持久的。
引理1 Rn+1+是系統(2)的正不變集。
證明 系統(2)等價于
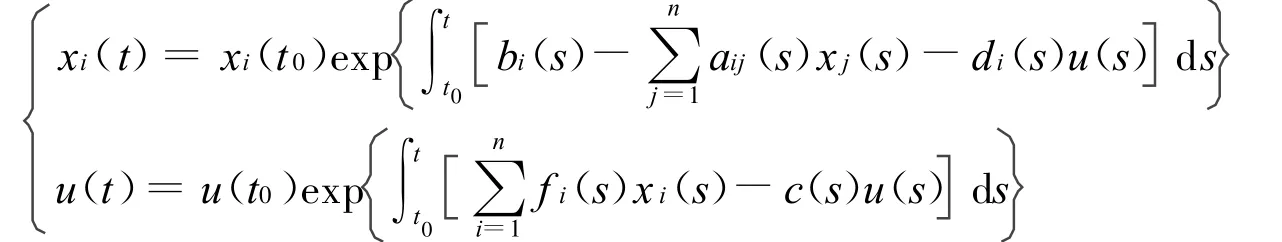
可見,當xi(t0)>0,u(t0)>0(t0≥0)時,必有xi(t)>0,u(t)>0,i=1,2,…,n。證畢。
證明 根據引理1,設(x(t),u(t))T=(x1(t),x2(t),…,xn(t),u(t))T是系統(2)滿足正初值條件(3)的任意解,由系統(2)的第一式有
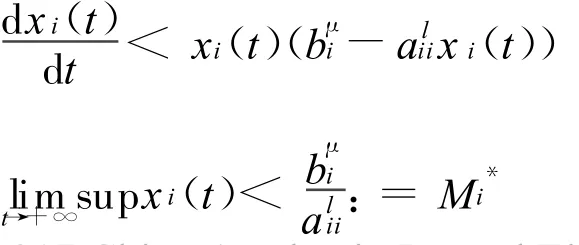
由比較定理知,存在T1>0,Mi≥M*i,當t>T1時,恒有xi(t)≤Mi,i=1,2,…,n。
當t>T1時,由系統(2)的第二式有

同樣地,存在T2>T1,R≥R*,當t>T2時,恒有u(t)≤R。
當t>T2時,由系統(2)的第一式有
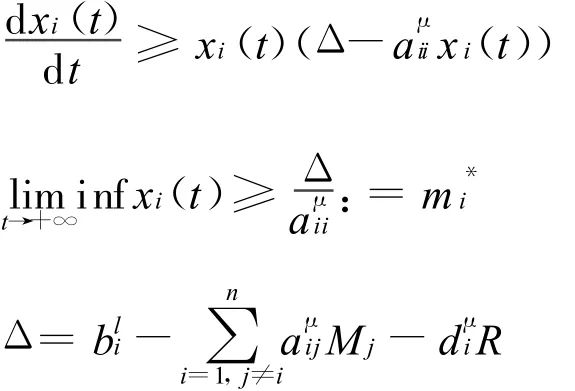
由比較定理知,存在T3>T2,m*i≥mi>0,當t>T3時,恒有xi(t)≥mi,i=1,2,…,n。
當t>T3時,由系統(2)的第二式有
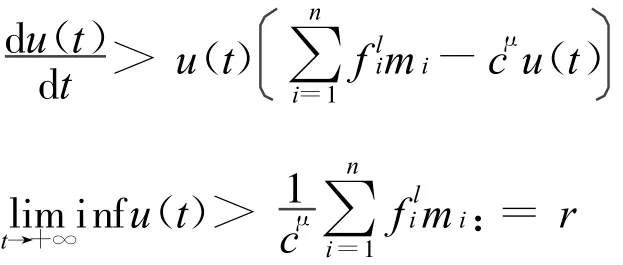
可知,存在T>T3,r*≥r>0,當t>T時,恒有u(t)≥r。
綜上,當t>T時,恒有
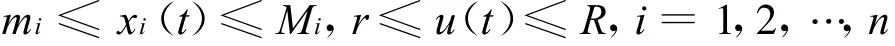
據此,獲得緊集
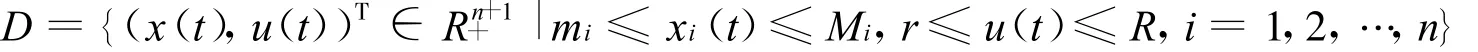
是系統(2)的正向不變集和最終有界區域。證畢。
2 全局吸引性
定義 2 設系統(2)的一個正解為(y(t),v(t))T,任意正解為(x(t),u(t))T,如果
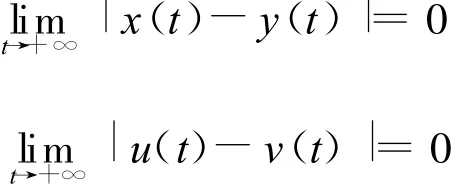
則稱系統(2)是全局吸引的。
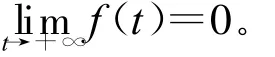
定理2 設系統(2)滿足正初值條件(2)和定理1條件,如果
證明 設系統(2)的一個正解為(y(t),v(t))T,任意正解為(x(t),u(t))T由定理1條件知,當t>T時,恒有mi≤xi(t),yi(t)≤Mi,r≤u(t),v(t)≤R,i=1,2,…,n。構造Lyapunov泛函
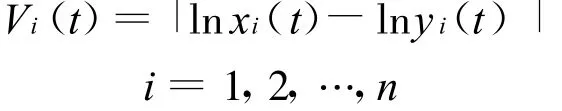
沿著系統(2)的解直接計算Vi(t)的右上導數,得到
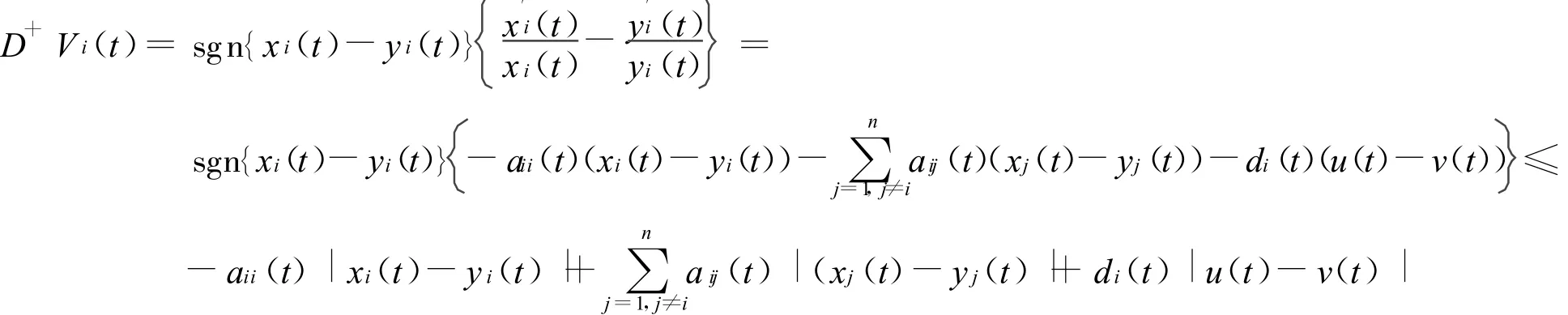
取Lyapunov泛函
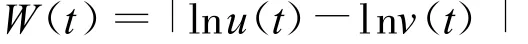
沿著系統(2)的解直接計算W(t)的右上導數,可得
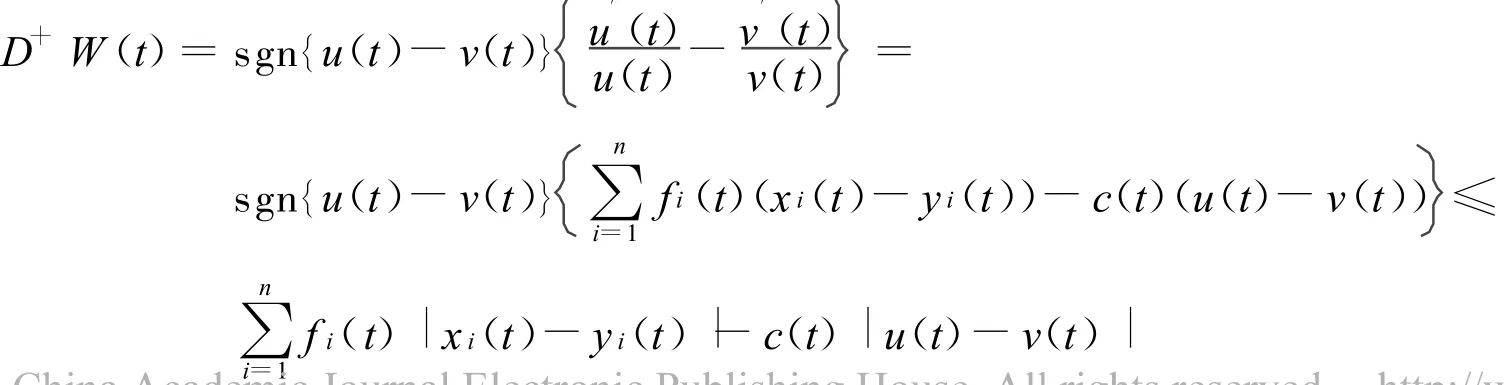
再構造Lyapunov泛函
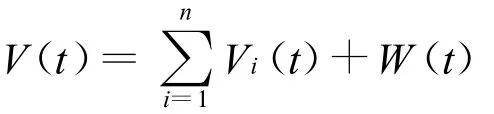
沿著系統(2)的解估計V(t)的右上導數,獲得

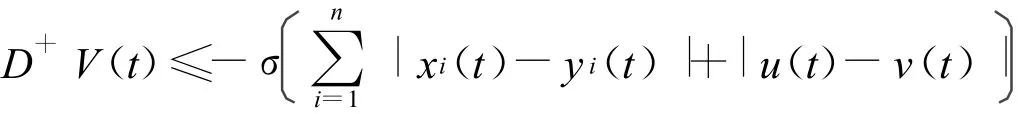
據此,從T到t積分得
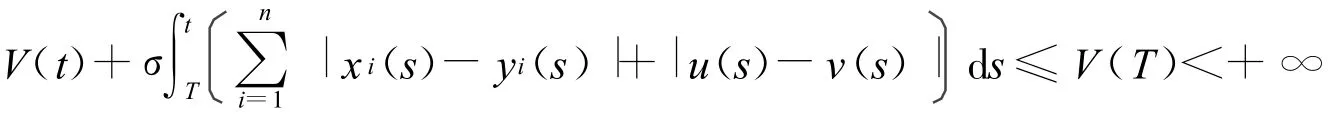
從而
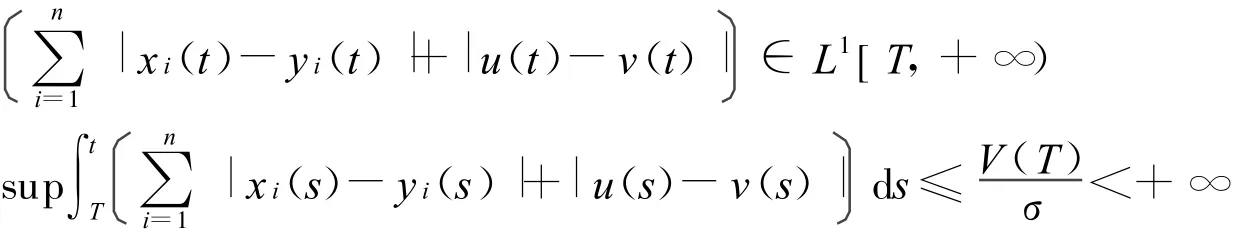
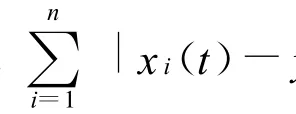
由引理2知
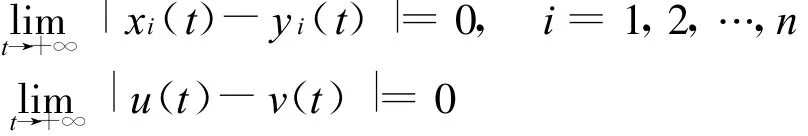
即
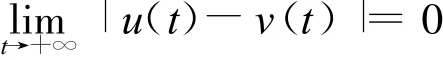
故系統(2)正解(y(t),v(t))T是全局吸引的。證畢。
3 應用舉例
根據系統(2),考慮如下具有生物控制的非自治兩種群Lotka-Volterra競爭系統:
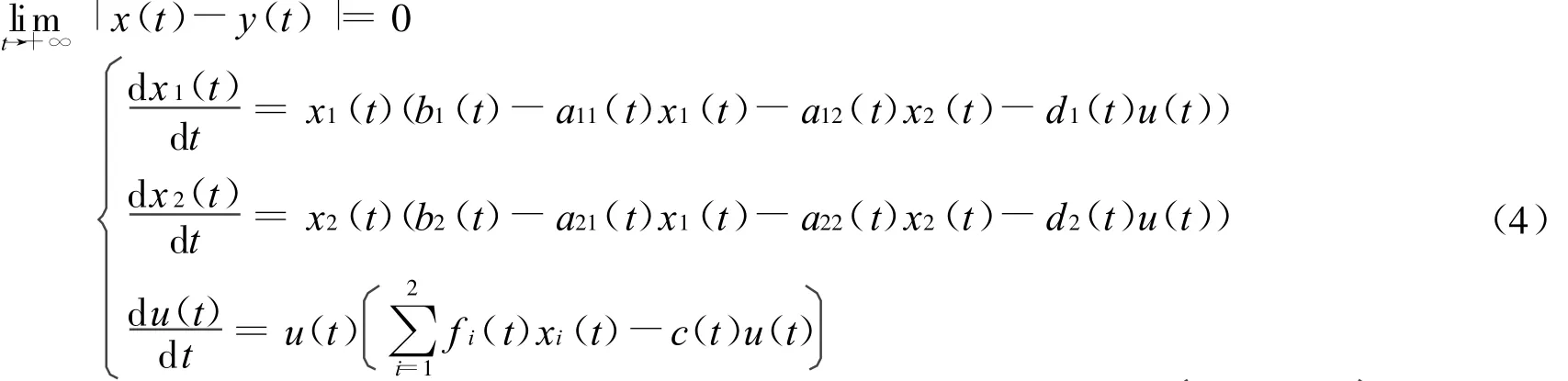
其中

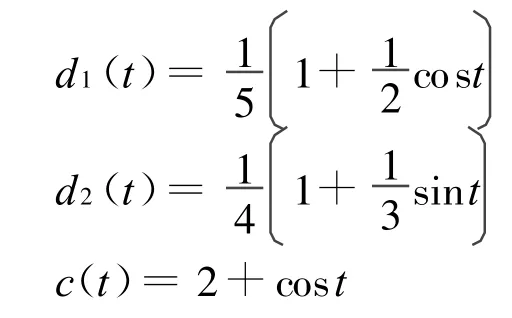
于是,有
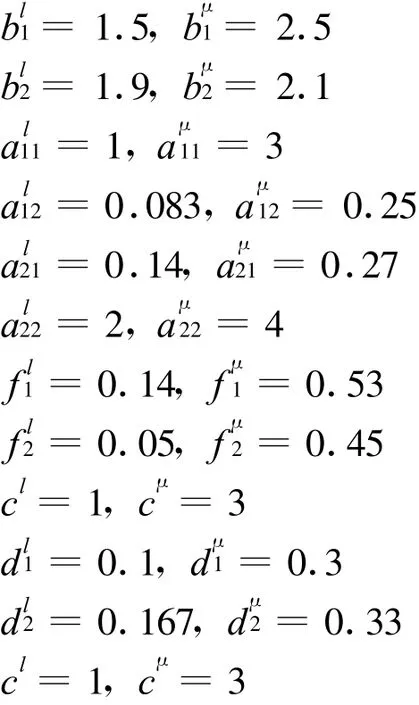
經計算,得到
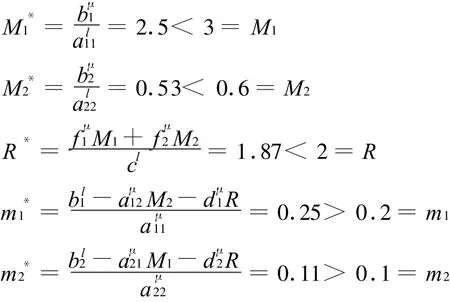
則由定理1知,系統(4)是一致持久的。
由于

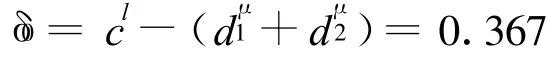
故由定理2知,系統(4)是全局吸引的。
[1] 陳蘭蓀,陳鍵.非線性生物動力系統[M].北京:科學出版社,1993:102-130.
[2] Ruan S,Xiao D.Global analysis in the predatorprey system with non-monotonic functional response[J].SIAM J.Appl.Math.,2001,61(1): 1445-1472.
[3] 程榮福,常亮.具無限時滯和非單調功能性反應捕食系統的多周期解[J].吉林大學學報:理學版,2010,48(5):761-765.
[4] 張正球,王志成.基于比率的三種群捕食者-食餌擴散系統的周期解[J].數學學報,2004,47(3):531-540.
[5] 黃玉梅.具HollingⅡ型功能反應的時滯擴散模型的全局穩定性[J].生物數學學報,2006,21(3):370-376.
[6] Gopalsamy K.Stability and oscillations in delay differential equation of population dynamics[M].Boston:Kluwer Academic Publishers,1992.
[7] Gopalsamy K,Weng Pei-xuan.Feedback regulation of logistic growth[J].Internat J Math.and Math. Sci.,1993,16:177-192.
[8] 程榮福,孫吉榮.具生物控制的時滯階段結構種群模型的穩定性[J].北華大學學報:自然科學版,2008,9(2):97-103.
[9] 程榮福.一類具生物控制的多滯量捕食模型正周期解的存在性[J].北華大學學報:自然科學版,2010,11(1):1-6.
[10] Barbalat I.System dequation differentilles doscilltion nonlinears[J].Rev.Math.Pure.Appl.,1959(4):267-270.

