光滑互補(bǔ)函數(shù)與互補(bǔ)問題的 2-正則解

俞昊東 ,徐翠霞 ,濮定國

(1.同濟(jì)大學(xué)應(yīng)用數(shù)學(xué)系,上海 200092;2.河南科技大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院,河南洛陽 471003)

0 前言

討論如下的非線性互補(bǔ)問題(記為NCP(F)):

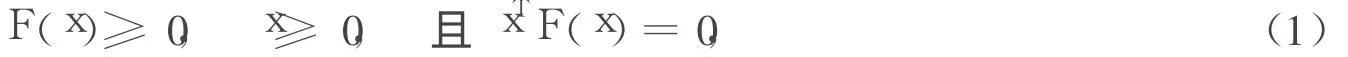
其中,x∈Rn,F:Rn→Rn是連續(xù)可微的非線性函數(shù)。對于互補(bǔ)問題的求解,最常用的求解途徑是利用如下的互補(bǔ)函數(shù)將其轉(zhuǎn)化為等價的非線性方程組。

定義1[1]對于二元函數(shù)φ:R2→R,若φ(a,b)=0當(dāng)且僅當(dāng)a≥0,b≥0,ab=0成立,則稱φ是一個互補(bǔ)函數(shù),或稱NCP函數(shù)。

最基本的NCP函數(shù)是φmin(a,b)=min{a,b}。利用互補(bǔ)函數(shù)可構(gòu)造如下方程組:

由NCP函數(shù)的定義易知,求解問題(1)等價于求解非線性方程組(2)。通常稱(2)為再生方程組。利用非線性方程組求解互補(bǔ)問題的方法,可參見文獻(xiàn)[1-2],求解非線性方程組全局解的方法可參見文獻(xiàn)[3]。

設(shè)x*是問題(1)的一個解,若存在某指標(biāo)i,使得=Fi(x*)=0,則稱x*是一個退化解。否則,稱x*是一個嚴(yán)格互補(bǔ)解,或非退化解。另一方面,對于再生方程組(2),若detφ′(x*)≠0(φ′(x)表示φ在x處的Jacobian陣),則稱x*是方程組(2)的一個正則解。反之,若φ′(x*)奇異,則稱它是一個奇異解。解的奇異性會給數(shù)值計算帶來本質(zhì)性的困難。例如,牛頓算法在奇異解的附近通常至多只能達(dá)到線性收斂性。

若互補(bǔ)函數(shù)φ是光滑的,則問題(1)的任一退化解x*必然是再生方程組(2)的一個奇異解。這種特性使得現(xiàn)今絕大多數(shù)求解互補(bǔ)問題的算法只能采用半光滑的互補(bǔ)函數(shù),因而所得到的再生方程組通常也只能是半光滑的。半光滑算法方面的性質(zhì)可參見文獻(xiàn)[1,4-5]。2-正則性條件處理奇異解問題的重要途徑,參見文獻(xiàn)[6-7]。對于互補(bǔ)問題來說,由于再生方程組在奇異解處通常只能對 φ′求方向?qū)?shù),而不存在二階導(dǎo)數(shù),因此文獻(xiàn)[8-9]提出了一類只利用 φ′的方向?qū)?shù)的 2-正則性。其定義如下:

定義2[8]令x*是方程組(2)的一個解,設(shè)φ()在x*的某鄰域內(nèi)可微,且導(dǎo)函數(shù)φ′方向可微。令P是從Rn到零空間kerφ′(x*)的正交投影算子,且定義集合

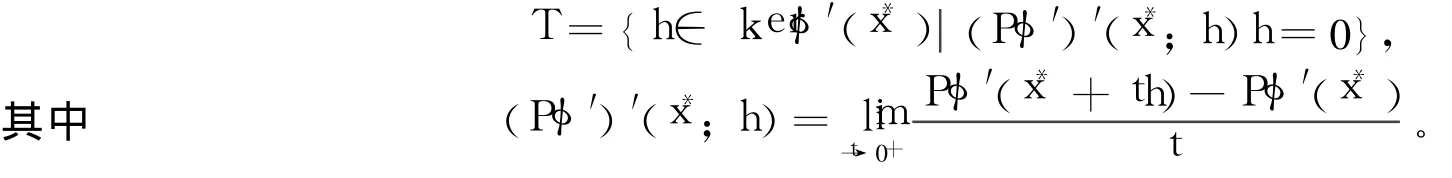
可以看出:若x*是(2)的正則解,則有kerφ′(x*)={0}。因此,x*必滿足2-正則性。從而2-正則性是正則性的一種推廣。這一概念的提出從理論上保證了可以設(shè)計出具有較好收斂性的光滑牛頓算法。

但對于 2-正則性的成立條件,已有文獻(xiàn)僅對個別函數(shù)進(jìn)行了討論,如文獻(xiàn)[8]研究了光滑互補(bǔ)函數(shù)φS(a,b)=2ab-{min(0,a+b)}2的性質(zhì),并證明了該函數(shù),若x*使互補(bǔ)問題(1)滿足b-正則性,則再生方程組在 x*成立 2-正則性。該文還對此結(jié)論的逆命題舉出了反例。

本文將文獻(xiàn)[8]的結(jié)果推廣到一般情形,在分析光滑互補(bǔ)函數(shù)有關(guān)性質(zhì)的基礎(chǔ)上,證明了只要該類函數(shù)具有二次正齊次性及其他一些很弱的條件,b-正則性就能保證再生方程的 2-正則性,同時,對于 φS成立的反例對于一般的光滑互補(bǔ)函數(shù)也是有效的,從而給出了 b-正則性和 2-正則性關(guān)系的一般性結(jié)論。說明了對于在實(shí)際計算中可用的大多數(shù)光滑 NCP函數(shù)來說,2-正則性都是一個合理且容易滿足的假設(shè)。

1 光滑NCP函數(shù)

光滑非線性互補(bǔ)函數(shù)有一些重要的性質(zhì)。

引理1 設(shè)互補(bǔ)函數(shù)φ(a,b)光滑,即它是連續(xù)可微的。則有:①對任意的a≥0,=0;②對任意的b≥0,=0。

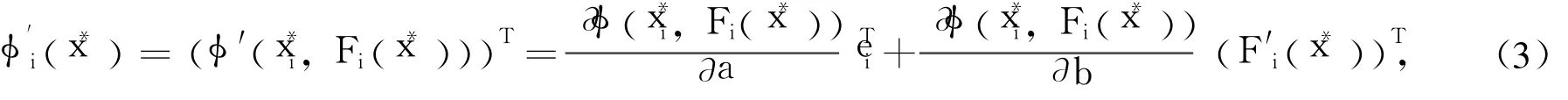
其中ei=(0,…,1,…,0)T(第i個分量為1)。則由引理1可得

因此,退化指標(biāo)所對應(yīng)的 φ′(x*)中的行向量等于0。由此立即得到以下結(jié)論。

引理2 若x*是問題(1)的退化解,則Jacobian陣φ′(x*)是奇異的。

2 二階正齊次函數(shù)

對一般二元函數(shù)的二次正齊次性給出定義如下。

定義3 對于二元函數(shù)φ(a,b):R2→R,若對任意t≥0都有φ(ta,tb)=t2φ(a,b),則稱函數(shù)φ(a,b)具有二次正齊次性。

特別注意到,若在上述定義中令 t=0,則有φ(0,0)=0。容易證明,具有二次正齊次的函數(shù)具有以下基本性質(zhì):

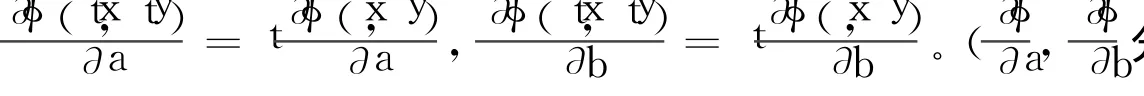
以下再給出此類函數(shù)的另一重要性質(zhì)。

證明 若(x,y)=(0,0),由于φ(0,0)=0,等式顯然成立。若(x,y)≠(0,0),不妨設(shè)x≠0。

(i)若x＞0,定義函數(shù)g1(s)∶=φ(1,s),s∈R。則由函數(shù)的二次正齊次性,φ(x,y)=x2φ(1,=x2g1()。因此,

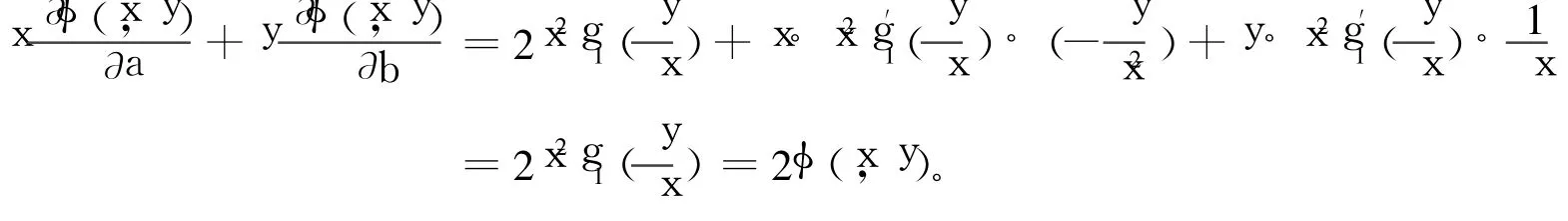
(ii)若x＜0,定義g2(s)∶=φ(-1,s),(s∈R)。由函數(shù)的二次正齊次性,φ(x,y)=x2g2(-)。同上可證得),故等式仍然成立。由上述(i)、(ii),命題成立。證畢。

分片線性的或一次的互補(bǔ)函數(shù)通常至多是半光滑的,因而光滑的互補(bǔ)函數(shù)一般至少是二次的。另一方面,若采用的互補(bǔ)函數(shù)次數(shù)過高,又會大大增加再生方程組的非線性化程度,給數(shù)值求解帶來困難。因而,對于實(shí)際算法中可用的大多數(shù)光滑互補(bǔ)函數(shù)來說,二次正齊次性是合理而基本的假設(shè)。

3 b-正則性與2-正則性

首先給出 b-正則性的定義如下,b-正則解的相關(guān)性質(zhì)可參見文獻(xiàn)[1,5]。

定義4[1]設(shè)x*是互補(bǔ)問題(1)的一個解,記G=F′(x*),若對任意子集α?δ?α∪β,主子陣 Gδδ非奇異,則稱 x*是互補(bǔ)問題的一個b-正則解。

容易看出,x*是b-正則解等價于以下條件成立:對集合β的任意剖分(A,B),即A∪B=β,A∩B=?及h∈Rn,都有

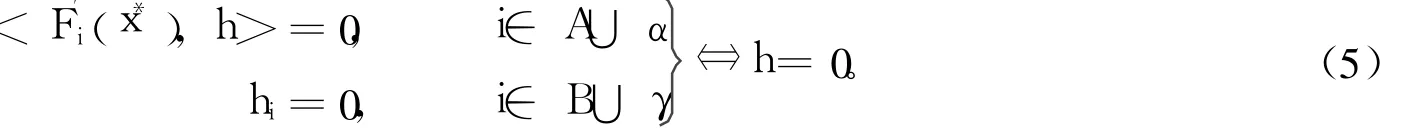
為討論b-正則解和2-正則性的關(guān)系,需對光滑互補(bǔ)函數(shù)φ(a,b)作如下假定:(A1)φ是二次正齊次函數(shù);(A2)≠0且≠0;(A3)導(dǎo)函數(shù)φ′方向可微(但一般不能假定可微)。

定理1 設(shè)x*是互補(bǔ)問題的一個b-正則解,若互補(bǔ)函數(shù)φ(a,b)是光滑的且滿足假設(shè)(A1)～(A3),則由此得到的再生方程組(2)在 x*滿足2-正則性。

證明 由于互補(bǔ)函數(shù)φ是光滑的且滿足假設(shè)(A3),且函數(shù)F(x)連續(xù)可微,易知φ′方向可微。由投影算子P的定義,若存在h∈Rn使(Pφ′)′(x*;h)h=0,則(φ′)′(x*;h)h∈imφ′(x*),其中, imφ′(x*)表示φ′(x*)的象空間。則由式(4)可得,對所有i∈β,都成立(φ)′(x*;h)h=0。故得T?T1∶={h∈kerφ′(x*)|(φ)′(x*;h)h=0,?i∈β}。因此,要證明2-正則性,只需證明T1={0}。任取i∈β,由式(3)及式(4),φ(x*)=0,且對任意h∈Rn及t＞0有φ(x*+th)=(F(x*+th))T。由Fi(x*)=0,得=＜F(x*),h＞。又顯然有F′i(x*+th)=(x*),故由引理3可知:

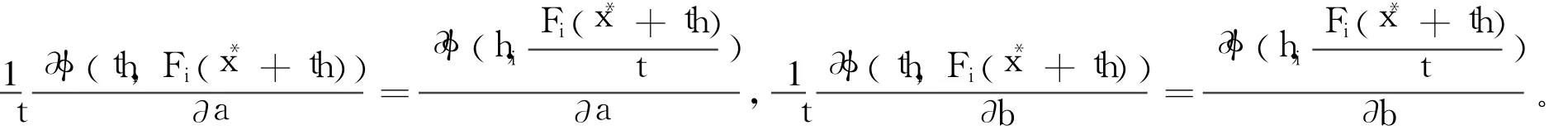
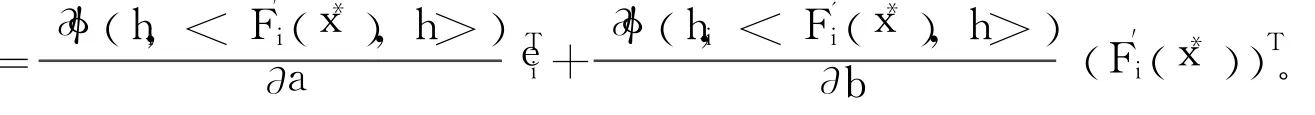
則由引理4可得:

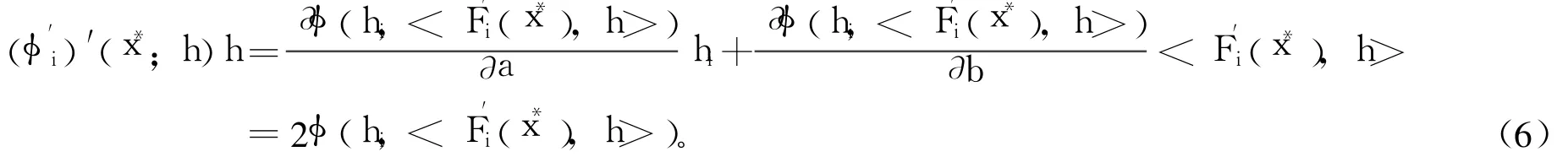
容易驗證,若條件(5)成立,則式(7)必成立,因此再生方程組(2)在x*成立2-正則性。證畢。

4 討論

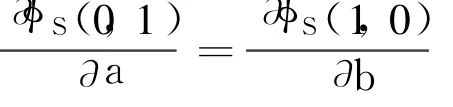
還可以新定義一類互補(bǔ)函數(shù)φM(a,b)=(a+b)-(a2+b2),顯然它也是二次正齊次的,并且

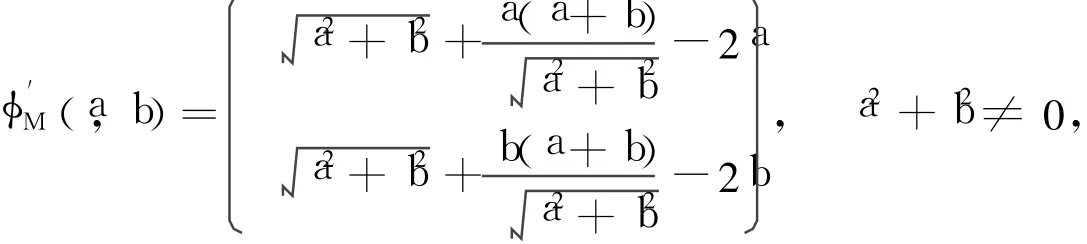
最后討論定理1的逆命題,即若x*是再生方程組(2)的2-正則解,它是否是互補(bǔ)問題的b-正則解。文獻(xiàn)[8]對于互補(bǔ)函數(shù) φS舉出了如下反例。

例1 在互補(bǔ)問題(1)中,令n=2,F(x)=(x1,-(x2-ρ)2)T,x∈R2,其中ρ＞0。該問題的唯一解是x*=(0,ρ)T。這是一個退化解,且β={1},α={2},γ=?。由條件(5)易知:b-正則性在x*不成立。

文獻(xiàn)[8]對 φS驗證了 x*是方程組(2)的 2-正則解。因此對于函數(shù) φS來說,例 1構(gòu)成了一個反例。這里給出對一般情形的討論,即對例 1有如下命題。

命題1 若互補(bǔ)函數(shù)φ是光滑的且滿足假設(shè)(A1)～(A3),且下列極限存在

則例1所對應(yīng)的再生方程組在x*有2-正則性。

證明 計算可得,φ′(x*)=0,故kerφ′(x*)=R2,從而投影矩陣P=I。由β={1}及式(6)易知:對任意h∈R2,(φ)′(x*;h)h=2φ(h1,h1)。因此,由()′(x*;h)h=0可知h1=0。

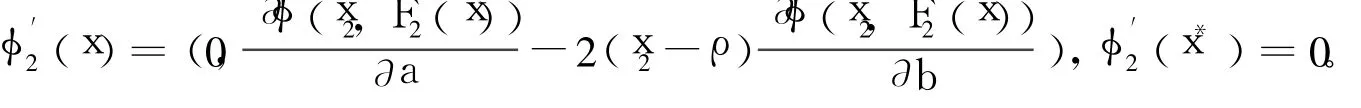
因此h=0,亦即T={0},從而x*是2-正則解。證畢。

命題1表明:例1對于滿足(A1)～(A3)且極限(8)存在的一大類光滑互補(bǔ)函數(shù)都是一個反例。容易驗證,φS和本文新提出的φM都符合命題 1的條件。因而,在一般意義上,2-正則性嚴(yán)格地弱于 b-正則性。

[1] 韓繼業(yè),修乃華,戚厚鐸.非線性互補(bǔ)理論與算法[M].上海:上海科學(xué)技術(shù)出版社,2006.

[2] 陳小君,張超.非線性方程組在幾類計算問題中的應(yīng)用[J].長沙理工大學(xué)學(xué)報:自然科學(xué)版,2006,3(4):1-7.

[3] 尚有林,楊森,王三良.無約束全局優(yōu)化的一個新凸填充函數(shù)[J].河南科技大學(xué)學(xué)報:自然科學(xué)版,2004,25(3):92-95.

[4] 濮定國,王華.集映射算子和半光滑性[J].同濟(jì)大學(xué)學(xué)報:自然科學(xué)版,2008,36(9):1278-1281.

[5] Facchinei F,Pang JS.Finite-dimensional Variational Inequalities and Comp lementarity Problems:Vol Iand Vol II[M].New York:Springer,2003.

[6]Oberlin C,W right S.An Accelerated Newton Method for Equations with Semismooth Jacobians and Nonlinear Complementarity Problems[J].Math Program:Ser B,2009,117:355-386.

[7] Griewank A.On Solving Nonlinear Equations with Simple Singularities or Nearly Singular Solutions[J].SIAM Rev,1985, 27(4):537-563.

[8] Izmailov A,Solodov M.Error Bounds for 2-regular Mappings with Lipschitzian Derivatives and their App lications[J].Math Program,2001,89(3):413-435.

[9] Daryina A,Izmailov A,Solodov M.AClass of Active-set New ton Methods forMixed Complementarity Problems[J].SIAM J Optim,2004,15(2):409-429.