約束優化問題的內點正則牛頓法

劉三明

(上海電機學院數理教學部,上海 200240)

0 前言

對于二次可微的強凸函數,Newton方向是下降方向,當初始點充分靠近極小點時,Newton法是收斂的。但當初始點遠離極小點時,其收斂性不能保證。為此,在牛頓法中引入步長因子,得到保證全局收斂的阻尼Newton法。當函數不是強凸函數時,Newton方向不一定是下降方向。為了保證Newton法的全局收斂性,對Hessian矩陣采用Levenberg-Marquardt正則化方法[1]。文獻[2]對Newton法提出了三次正則化方法。在每次迭代時,只需求解 1個與牛頓法相同的二次函數的無約束最優化問題,但其正則項是三次的。

文獻[3]中提出了一種求解無約束凸規劃最優解的正則Newton法,該方法不要求函數是強凸的,且具有全局收斂性。在正則 Newton法中,凸函數在一點的正則化基于近似點算法[3-6],而近似參數取為該點梯度的模,即凸函數f(x)在點x處的正則化函數為:

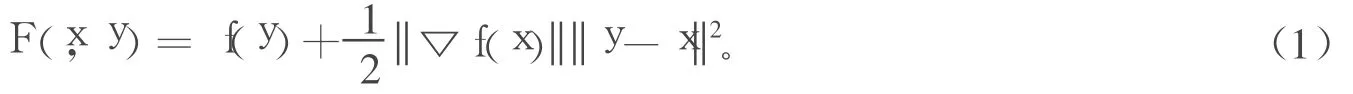
通過上述方法,文獻[7]給出了求解任意凸規劃minx∈Rnf(x)的具有全局收斂性的Newton法。

本文考慮具有不等式約束的凸規劃問題:

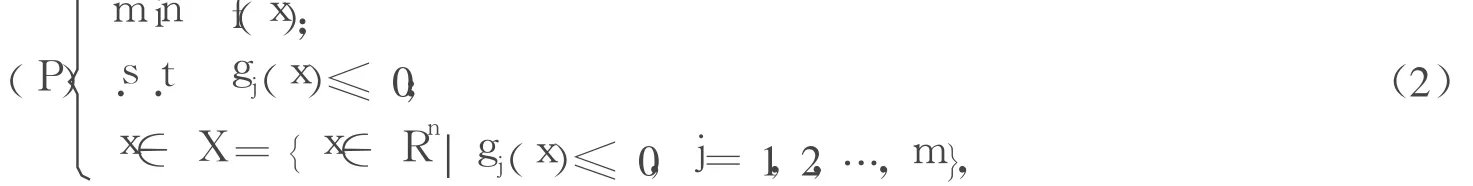
其中,x∈Rn,f,gj(j=1,2,…,m):Rn→R是凸函數。

對凸規劃問題(P),把對數障礙函數法同正則Newton法結合起來,提出了求解具有不等式約束的凸規劃問題(P)的內點正則Newton法。可以證明該算法具有全局收斂性。

1 內點正則New ton法的建立

對問題(P),作如下假設(A):

(1)f,gj(j=1,2,…,m):Rn→R是二階連續可微的凸函數。(2)int X={x∈Rn|gj(x)＜0,j=1,2,…,m}是非空的。(3)問題(P)的最優解集X*是非空的緊集。(4)存在x∈ int X。

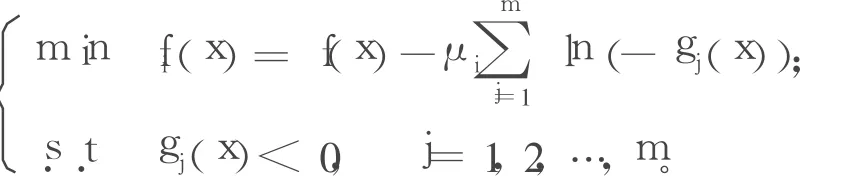
用f*記問題(P)的最優目標函數值,記問題(P1)的最優目標函數值,下面給出求解問題(P)的內點正則Newton法。

內點正則Newton法:步1,取μ1＞0,0＜β＜1,x0∈int X,ε1＞0。

步2,對i=1,2,…,定義如下問題:

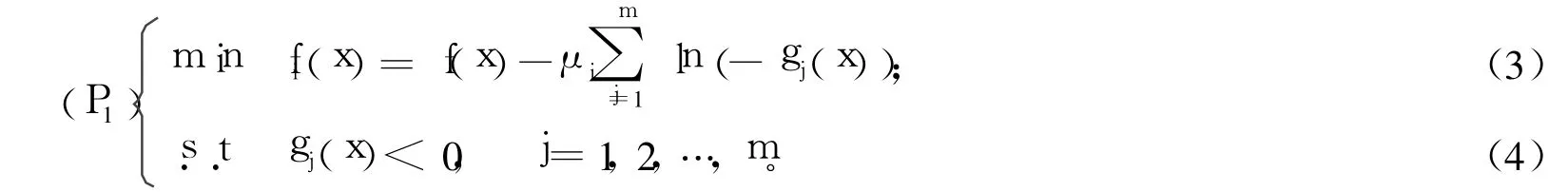
步3,對k=1,2,…,定義

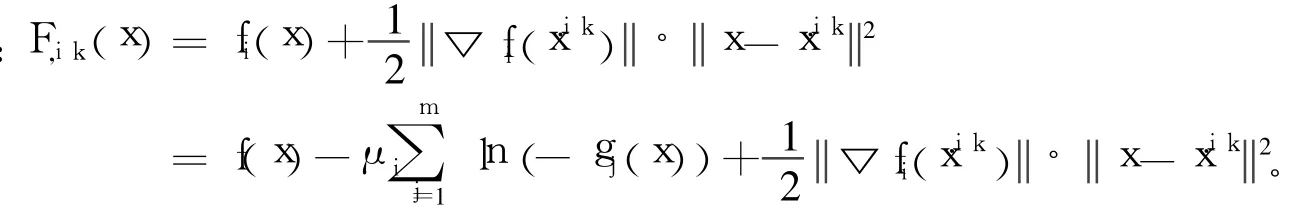
步4,內循環:求解問題(P1)。①置xi,0=xi-1,若≤εi,則置εi+1=,xi=xi,0,轉步5,退出內循環;否則,轉②,繼續進行內循環。②計算New ton方向s(xi,k)=-[▽2fi(xi,k)+I]-1▽fi(xi,k)。③用Armijo準則確定步長αi,k使得:fi(xi,k+αi,ks(xi,k))≤fi(xi,k)+ραi,k▽fi(xi,k)Ts(xi,k)且xi,k+αi,ks(xi,k)∈int X,其中0＜ρ＜1,αi,k＞0。記xi,k+1=xi,k+αi,ks(xi,k)。④若＞εi,令k∶=k+1,xi,k=xi,k+1,轉②,繼續對k進行內循環;否則,置εi+1=,xi= xi,k+1,轉步 5,退出內循環。

步5,令μi+1=βμi,置i=i+1,μi∶=μi+1。轉步2。

2 收斂性分析

為了證明內點正則Newton法的收斂性,還需作如下假設(B):

(1)對任意x,y∈X,f(x)、gj(x)(j=1,2,…,m)滿足≤L≤L, j=1,2,…,m。

(2)對任意x∈X,以及y∈Rn,存在0≤n(x)＜N(x)＜+∞,使得:

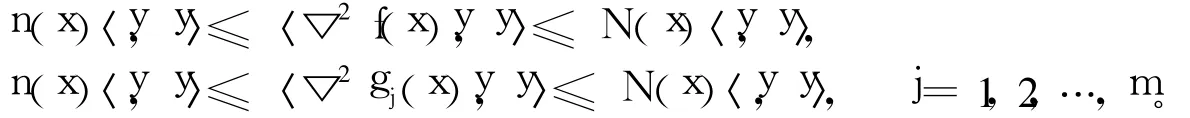
(3)對每個緊集S?X,存在0＜C2S＜C1S＜+∞滿足:

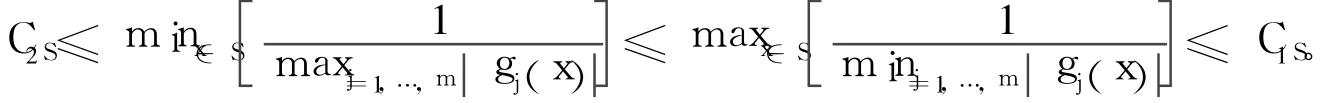
引理1 設問題(P)滿足條件(A)和條件(B),對任意x0∈int X,記Ω={x∈Rn:fi(x)≤fi(x0), gj(x)＜0(j=1,2,…,m)},則存在M0＞0,L0＞0,使得:

證明 由Ω是緊集及問題(P)滿足條件(A)和條件(B)可證。

引理2 設問題(P)滿足條件(A)和條件(B),對任意x0∈int X,記Ω={x∈Rn:fi(x)≤fi(x0), gj(x)＜0(j=1,2,…,m)},則:

(1)對任意x∈Ω,y∈Rn,有n(x)〈y,y〉≤〈▽2fi(x)y,y〉。

證明 由Ω是緊集及問題(P)滿足條件(A)和條件(B)可證。

定理1 設問題(P)滿足條件(A)和條件(B),則內點正則Newton法的內循環在有限步后終止。

因為對任意x,y∈X,有fi(x+y)=fi(x)+∫10〈▽fi(x+τy),y〉dτ,所以可得:

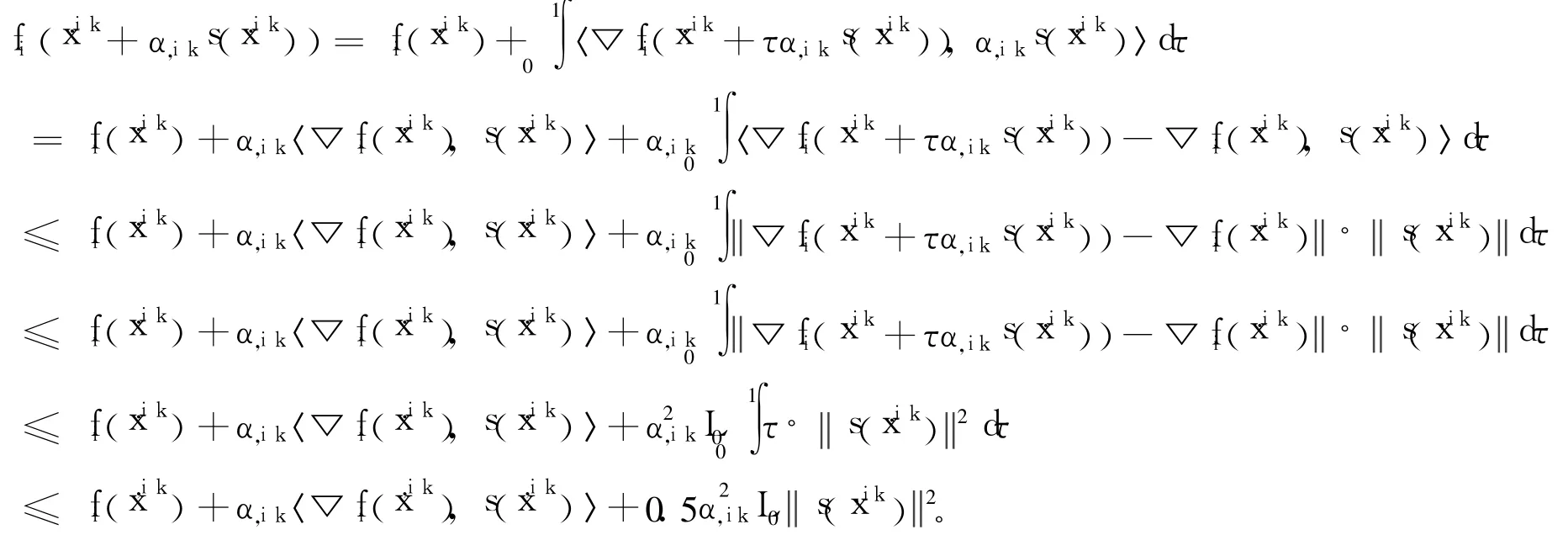
由s(xi,k)=-[▽2fi(xi,k)+▽fi(xi,k)I]-1▽fi(xi,k),得[▽2fi(xi,k)+▽fi(xi,k)I]s(xi,k)=-▽fi(xi,k),從而有〈[▽2fi(xi,k)+▽fi(xi,k)I]s(xi,k),s(xi,k)〉=-〈▽fi(xi,k),s(xi,k)〉,所以:

由引理2的結論1知:

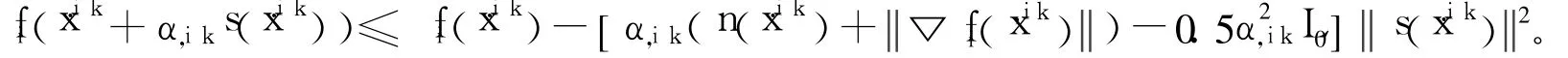
取αi,k=θ(n(xi,k)+▽fi(xi,k))L,其中0＜θ≤1,且使αi,k滿足Armijo準則,所以有:

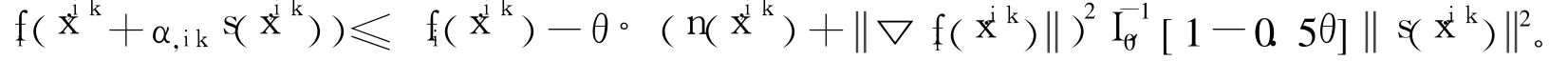
因為[▽2fi(xi,k)+▽fi(xi,k)I]s(xi,k)=-▽fi(xi,k),所以:

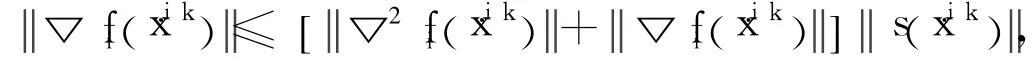
從而可得:

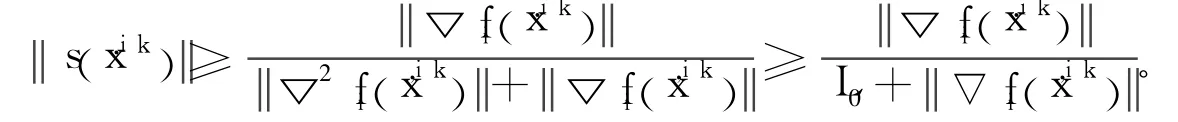
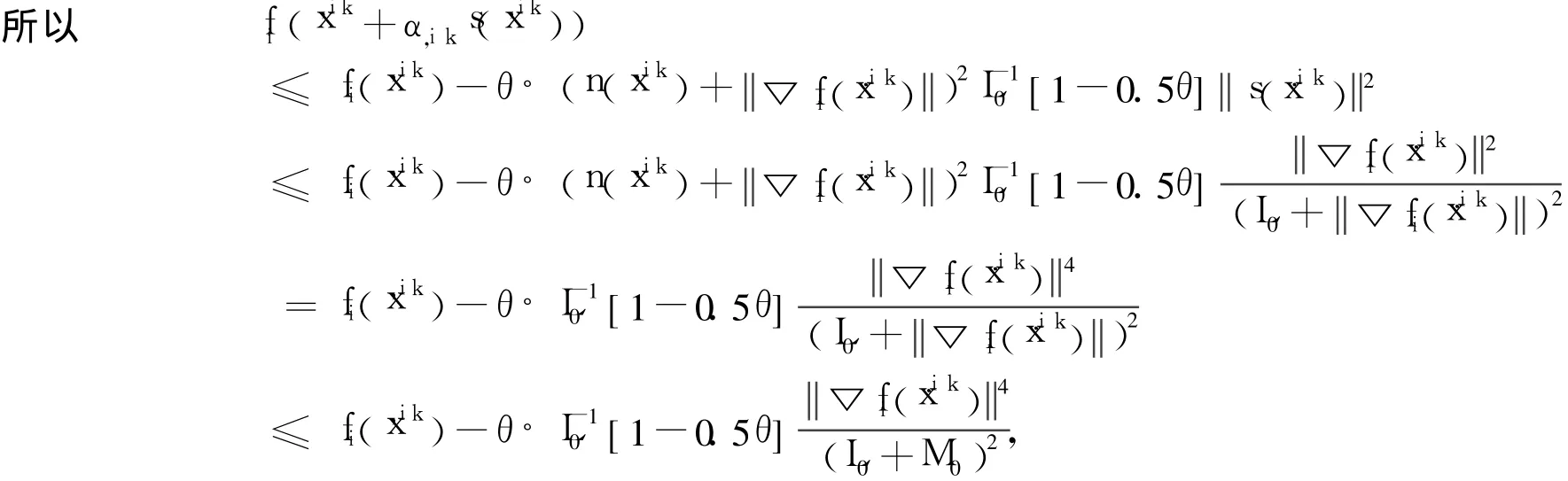
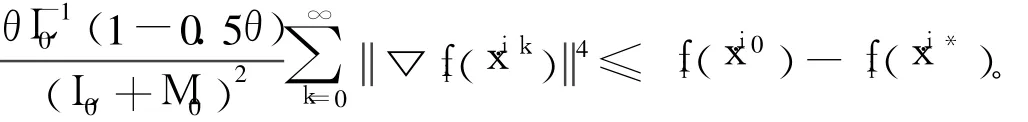
定理2 設問題(P)滿足條件(A)和條件(B),則內點正則Newton法產生的點列{xi}至少有一個聚點,且{xi}的每個聚點都是問題(P)的最優解。

證明 由定理1知:對每個i∈{1,2,…}內循環在有限步后終止,且由內點正則New ton法知產生的點列{xi}屬于水平集Ω={x∈Rn:fi(x)≤fi(x0),gj(x)＜0 (j=1,2,…,m)}。由文獻[3]知Ω是緊集,所以點列{xi}有聚點,下面證明{xi}的每一個聚點都是問題(P)的最優解。

設x*是{xi}的聚點,不妨設{xij}是{xi}的收斂子列,且jl→im∞xij=x*,x*∈Ω。由內點正則New ton法知▽fij(xij≤εij且εij=。設是問題(P1)當i=ij時的最優解,因為fij(x)是可微的凸函數,所以:

即:

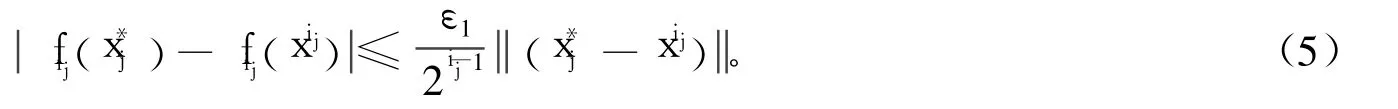
又因為內點正則Newton法產生的點列{xi}中的每一點xi均屬于緊水平集Ω={x∈Rn:fi(x)≤fi(x0), gl(x)＜0 (l=1,2,…,m)},所以xij-x**是有界的。又因為=x**,所以-x**有界。從而存在C＞0使得xij-≤C。在式(5)中讓j→+∞,得:

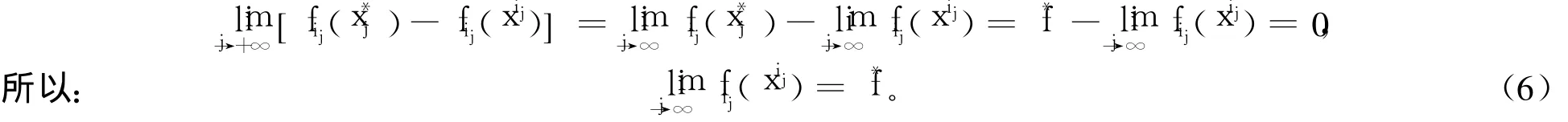
下面證明{xij}收斂到問題(P)的最優解。由xij=x*,x*∈Ω及f(x)、gl(x)(l=1,2,…,m)的連續性得f(xij)=f(x*),(xij)=gl(x*)由式(6)及fij(x)的表達式知(-gl(xij))

存在且有:

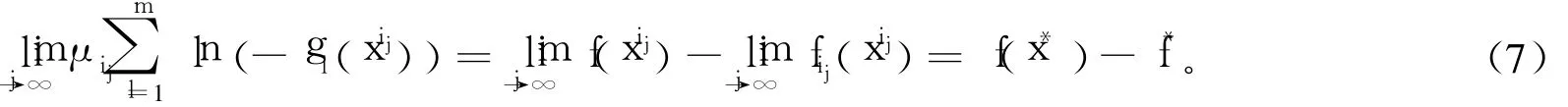
3 結論

對具有不等式約束的凸規劃問題,通過把對數障礙函數法同正則Newton法結合起來,構造了求解具有不等式約束的凸規劃問題的內點正則 Newton法,并證明了該算法具有全局收斂性。

[1] Nocedal J,W right SJ.Numerical Op timization[M].北京:科學出版社,2006.

[2]Nesterov Y,Polyak B T.Cubic Regularization of Newton Method and Its Global Performance[J].Mathematical Programming,2006,108(1):177-205.

[3] Kantorovich L V.Functional Analysis and Applied Mathematics[J].Uspekhi Mat Nauk,1948,3(6):89-185.

[4] Guler O.New Proximal Point Algorithms for Convex Minimization[J].SIAM Journalon Optimization,1992,2:649-664.

[5] Bernard F,Thibault L.Prox-regularity of Functions and Sets in Banach Spaces[J].Set-Valued Anal,2004,12(1):25-47.

[6] Bernard F,Thibault L.Prox-regular Functions in H ilbert Spaces[J].Journal of Mathematical Analysis and Application, 2005,303(1):1-14.

[7] Polyak R A.Regularized Newton Method for Unconstrained Convex Optimization[J].Math Program:Ser B,2009,120(1): 125-145.

[8] 袁亞湘,孫文瑜.最優化理論與方法[M].北京:科學出版社,1999.