函數(shù)連續(xù)性與一致連續(xù)性的探討

周明益 （揚(yáng)州工業(yè)職業(yè)技術(shù)學(xué)院基礎(chǔ)部，江蘇揚(yáng)州225000）

函數(shù)的一致連續(xù)性是數(shù)學(xué)分析課程中的一個(gè)重要內(nèi)容，函數(shù)f（x）在某區(qū)間內(nèi)連續(xù)，是指函數(shù)f（x）在該區(qū)間內(nèi)每一點(diǎn)都連續(xù)，它反映函數(shù)f（x）在該區(qū)間上一點(diǎn)附近的局部性質(zhì)，但函數(shù)的一致連續(xù)性則反映的是函數(shù)f（x）在給定區(qū)間上的整體性質(zhì)，它有助于研究函數(shù)f（x）的變化趨勢(shì)及性質(zhì)。現(xiàn)有的數(shù)學(xué)分析教材中，一般只給出函數(shù)一致連續(xù)的概念和判定函數(shù)在閉區(qū)間上一致連續(xù)的康托定理，內(nèi)容篇幅少，為了對(duì)函數(shù)一致連續(xù)性的理論有正確的理解和全面的掌握，筆者對(duì)函數(shù)一致連續(xù)性的概念、判定條件以及兩者之間的聯(lián)系進(jìn)行了深入的分析和總結(jié)。

1 函數(shù)連續(xù)的局部性

定義1函數(shù)f（x）在∪（x0）內(nèi)有定義，則函數(shù)f（x）在點(diǎn)x0連續(xù)是指 ?ε＞0，?δ＞0，使得當(dāng)｜x-x0｜＜δ時(shí)，有：

函數(shù)f（x）在點(diǎn)x0處連續(xù)，是否意味著f（x）在x0的鄰域內(nèi)連續(xù)呢？或者說其圖象在此鄰域上連綿不斷呢？回答是否定的[1]。如函數(shù)y＝xD（x）只在x＝0連續(xù)；函數(shù)y＝（x-1）（x-2）D（x）僅在x＝1，x＝2連續(xù)；又如函數(shù)：

容易證明這個(gè)函數(shù)在任意點(diǎn)是連續(xù)的，卻不能一筆畫出函數(shù)在x＝0的任意小鄰域內(nèi)的圖形。上述例子表明“連續(xù)”僅僅是一個(gè)局部概念，不能僅從字面去理解f（x）在x0連續(xù)。當(dāng)且僅當(dāng)f（x）在x0的鄰域∪（x0，δ）內(nèi)每一點(diǎn)都連續(xù)，才能說f（x）在x0的鄰域內(nèi)連續(xù)。函數(shù)在點(diǎn)x0處連續(xù)的定義不能完全反映“連續(xù)”二字的本意。但是，如果在連續(xù)點(diǎn)x0的函數(shù)值f（x0）≠0，那么上述情形就不會(huì)出現(xiàn)。

命題1設(shè)f（x）在x0連續(xù)，且f（x0）≠0，則一定存在x0的某個(gè)鄰域，使f（x）在此鄰域內(nèi)連續(xù)。

證明因f（x）在點(diǎn)x0連續(xù)，即 ?ε＞0，?δ＞0，使得 ?x∈∪（x0；δ）有：

現(xiàn)對(duì) ?x′∈∪（x0；δ），由式（3）顯然有：

又f（x0）≠0，當(dāng)δ充分小時(shí)，由局部保號(hào)性有：

即f（x′）≠0，從而有：

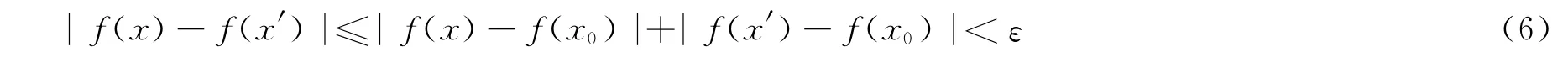
可見f（x）在x′連續(xù)，由x′的任意性，知f（x）在x0的δ鄰域內(nèi)連續(xù)。

因此，函數(shù)的連續(xù)性是一種按點(diǎn)而言的連續(xù)性，它僅僅反映了函數(shù)在區(qū)間上一點(diǎn)附近的局部性質(zhì)。

2 函數(shù)一致連續(xù)的整體性

連續(xù)函數(shù)以它具有一系列良好的性質(zhì)而成為數(shù)學(xué)分析研究的主要對(duì)象，然而在連續(xù)函數(shù)中，又以一致連續(xù)的函數(shù)最為重要。因此，判定一個(gè)函數(shù)在其定義域內(nèi)是否一致連續(xù)，是數(shù)學(xué)分析的一個(gè)重要內(nèi)容之一。

定義2設(shè)函數(shù)f（x）在區(qū)間I上有定義，若對(duì) ?ε＞0，?δ＝δ（ε）＞0，?x′，x″∈I，只要｜x′-x″｜＜δ，有：

則稱函數(shù)f（x）在區(qū)間I上一致連續(xù)[2]。

定義2中的“一致”指的是什么呢？只要與函數(shù)f（x）在區(qū)間I上連續(xù)的定義進(jìn)行比較，不難發(fā)現(xiàn)，連續(xù)定義中的δ，不僅僅依賴于ε，還依賴于點(diǎn)x0在區(qū)間I中的位置，即δ＝δ（ε；x0）；而f（x）在I上一致連續(xù)是指，存在這樣的δ，它只與ε有關(guān)而與x0在區(qū)間I中的位置無關(guān)，即δ＝δ（ε）。也就是說，如果函數(shù)f（x）在區(qū)間I上連續(xù)，則對(duì)任意給定的正數(shù)ε，對(duì)于I上的每一點(diǎn)x0，都能分別找到相應(yīng)的正數(shù)δ，使得對(duì)I上的任意一點(diǎn)x，只要｜x-x0｜＜δ，就有｜f（x）-f（x0）｜＜ε，其中δ＝δ（ε；x0）。對(duì)于同一個(gè)ε而言，當(dāng)x0在I上變動(dòng)時(shí)，δ的大小一般也隨著改變，即δ依賴于x0。

如果δ的大小只與給定的ε有關(guān)，而與點(diǎn)x0在I上的位置無關(guān)，那么這時(shí)f（x）就在I上一致連續(xù)。可見“一致”指的就是存在適合于I上所有點(diǎn)x的公共δ，即δ＝δ（ε）。直觀地說，f（x）在I上一致連續(xù)意味著：不論兩點(diǎn)x′與x″在I中處于什么位置，只要它們的距離小于δ，就可以使｜f（x′）-f（x″）｜＜ε。

這里可能會(huì)產(chǎn)生這樣的疑問：既然對(duì)I中每一個(gè)點(diǎn)x0都能找出相應(yīng)的δ（ε；x0），那么取這些δ（ε；x0）的最小者或者是下確界作為正數(shù)δ（ε），不就能使其與點(diǎn)x0無關(guān)了嗎？事實(shí)上，這不一定能辦得到。因?yàn)閰^(qū)間I中有無窮多個(gè)點(diǎn)，從而一般地也對(duì)應(yīng)著無窮多個(gè)正數(shù)δ（ε；x0），這無窮多個(gè)正數(shù)卻未必有最小的正數(shù)或取下確界為零[3]。

所以，f（x）在區(qū)間I上一致連續(xù)，反映出f（x）在I上各點(diǎn)“連續(xù)”程度是否步調(diào)“一致”這樣一個(gè)整體性質(zhì)。

3 函數(shù)連續(xù)性與一致連續(xù)性的聯(lián)系

函數(shù)f（x）在區(qū)間I上連續(xù)與一致連續(xù)是2個(gè)不同的概念，但它們之間也有聯(lián)系。

命題2[4]函數(shù)f（x）在區(qū)間I上一致連續(xù)，則f（x）在I上連續(xù)。

命題2的證明是顯然的，只須將其中的一個(gè)點(diǎn)（x′或x″）固定即可，但命題2的逆命題卻不一定成立。

例1證明函數(shù)在（0，1）內(nèi)不一致連續(xù)（盡管它在（0，1）內(nèi)每一點(diǎn)都連續(xù)）。

證明取ε0＝1，對(duì)?δ＞0（δ充分小且不妨設(shè)），取，則：

但：

命題3在閉區(qū)間[a，b]上連續(xù)的函數(shù)f（x）在[a，b]上一致連續(xù)。

這是著名的G.康托定理。閉區(qū)間上連續(xù)函數(shù)的這一性質(zhì)對(duì)研究函數(shù)的一致連續(xù)性十分重要，由它可以推出許多重要的結(jié)論。

注1對(duì)函數(shù)的一致連續(xù)性概念的掌握，應(yīng)注意以下3個(gè)方面[5]。

1）函數(shù)在區(qū)間的連續(xù)性與一致連續(xù)性的區(qū)別和聯(lián)系。

2）函數(shù)一致連續(xù)的實(shí)質(zhì)，是區(qū)間上任意2個(gè)彼此充分靠近的點(diǎn)的函數(shù)值的差的絕對(duì)值可以任意小，即對(duì) ?x′，x″∈I，當(dāng)｜x′-x″｜＜δ時(shí)，就有：

3）函數(shù)一致連續(xù)的否定敘述：設(shè)函數(shù)f（x）在區(qū)間I上有定義，若?ε0＜0，使?δ＞0，總?x′，x″∈I，雖然有：

但是：

則稱函數(shù)f（x）在區(qū)間I上非一致連續(xù)。

通過以上分析得出，可以在一點(diǎn)處討論函數(shù)的連續(xù)性，卻不能在一點(diǎn)處討論函數(shù)的一致連續(xù)性，函數(shù)的連續(xù)性反映的是函數(shù)的局部性質(zhì)，而函數(shù)的一致連續(xù)性則反映的是在整個(gè)區(qū)間上的整體性質(zhì)。

[1]李鋒杰，劉丙辰.關(guān)于函數(shù)的一致連續(xù)問題[J].煙臺(tái)師范學(xué)院學(xué)報(bào)，2001（4）：305-307.

[2]劉玉璉，傅沛仁.數(shù)學(xué)分析講義[M].第2版.北京：高等教育出版社，2003：135-144.

[3]周家云，劉一鳴，解際太.數(shù)學(xué)分析的方法[M].濟(jì)南：山東教育出版社，1991：52-56.

[4]林遠(yuǎn)華.對(duì)函數(shù)一致連續(xù)性的幾點(diǎn)討論[J].河池師專學(xué)報(bào)，2003（12）：68-70.

[5]姜雄.關(guān)于函數(shù)在任意區(qū)間上一致連續(xù)與非一致連續(xù)的條件討論[J].遼寧科技學(xué)院學(xué)報(bào)，2005（2）：35-36.