一元冪指函數的微積分性質及應用

張勇軍，何文峰，符一平

(海南大學信息科學技術學院，海南 海口 570228)

一元冪指函數的微積分性質及應用

張勇軍，何文峰，符一平

(海南大學信息科學技術學院，海南 海口 570228)

冪指函數是一類非常重要的函數，它在實際生活中會經常遇到。因此，更進一步的了解和掌握冪指函數的各種性質，對解決一些實際問題非常的重要。介紹了冪指函數的一些微分性質。

冪指函數；微分；積分；性質

《數學分析》和《高等數學》教材中對于冪指函數的內容非常少，僅僅只給出了冪指函數的定義[1]及一些求導公式[2]，而且例題與課后的習題也很少。然而在其他的一些教材、參考資料以及近幾年的研究生入學考試中卻又經常出現，于是對冪指函數的性質更進一步的了解與掌握是非常必要的。筆者就冪指函數的微積分性質進行了一些研究及應用。

1 一元冪指函數的微分性質

定理1一元冪指函數y=u(x)v(x)(u(x)>0,u(x),v(x)均為可微函數)的微分公式為：

dy=[u(x)]v(x)[v(x)lnu(x)]′dxd2y=[u(x)]v(x){[v(x)lnu(x)]″+[v(x)lnu(x)]′2}dx2

d3y=[u(x)]v(x){[v(x)lnu(x)]?+3[v(x)lnu(x)]″[v(x)lnu(x)]′+[v(x)lnu(x)]′3}dx3

……

dn+1y={[u(x)]v(x)[v(x)lnu(x)]′}(n)dxn+1

證明

dy=d[u(x)v(x)]=[u(x)v(x)]′dx=[u(x)v(x)][v(x)lnu(x)]′dx

={[u(x)v(x)]{[v(x)lnu(x)]?+([v(x)lnu(x)]′2)′}

+{[v(x)lnu(x)]″+[v(x)lnu(x)]′2}[u(x)v(x)]′}dx3

2 一元冪指函數的積分性質

定理2若u(x),v(x)為可微函數，且u(x)>0，則:

證明因u(x),v(x)為可微函數，且u(x)>0,故:

3 應 用

例1設y=xx(x>0),求dy,d2y,d3y,…,dn+1y。

解由定理1得：

dy=xx(xlnx)′dx=xx(1+lnx)dx

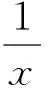
解法2利用冪指函數xx+1的微分變形:

[1]同濟大學數學系.高等數學(上冊)[M]. 第6版.北京：高等教育出版社，2007:102-106.

[2]華東師范大學數學系.數學分析(上冊)[M]. 第3版.北京：高等教育出版社，2001：101.

[3]徐文雄.高等數學(上冊)[M].北京：高等教育出版社，2004：85，183.

[編輯] 洪云飛

10.3969/j.issn.1673-1409.2011.09.003

O157.1

A

1673-1409(2011)09-0006-02