量子力學中算符微商淺析
李新克
(湖北汽車工業學院科技學院,湖北 十堰 442002)
量子力學中算符微商淺析
李新克
(湖北汽車工業學院科技學院,湖北 十堰 442002)
結合具體例子,介紹了量子理論中幾種不同情況下算符微商的定義、運算法則和計算方法,以幫助學生掌握算符的微商運算。
量子力學;算符運算;微商
量子系統的運動狀態用態矢量描述,而物理量則需要用相應的線性厄米算符作用到態矢量上獲得[1]。算符的運算方法與數字的運算方法有很大不同,常常成為學習量子理論的攔路虎。而在量子力學、量子光學等學科的學習當中,經常會遇到算符微商的問題[2],但是許多教材都沒有詳細討論,致使一些學生在學習時遇到更多困難。下面,筆者分別討論幾種不同情形下的算符微商問題?。
1 算符對時間的微商

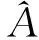
與平均值定義比較可得:

2 含參變量算符對參變量的微商
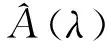
如果把算符寫作矩陣形式,算符的微商即為對算符矩陣元的微商。利用這個定義可以很容易證明算符對參變量微商的一些運算法則。以經常遇到的指數形式算符為例[6],設:
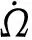

(1)
在海森堡繪景下利用式(1)可以很容易推導海森堡方程[6]:
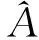
相應的,如果把式(1)看做微分方程,其解即為:
(2)
式中,c為常數。
3 算符函數對算符的微商
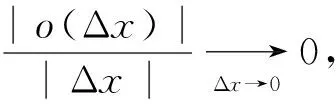

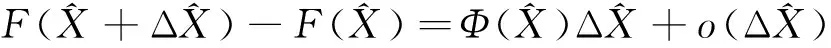
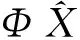
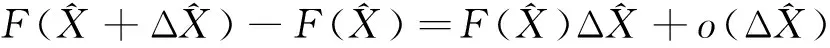
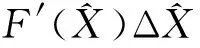
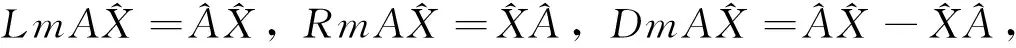
可得:
4 結 語
介紹了量子理論中算符和算符函數微商在幾種常見情況下的定義和運算法則,并舉例進行了說明。在了解和掌握這些內容之后,算符微商的問題就會逐漸地得心應手,能大大提高量子理論的學習效率。
[1]狄拉克.量子力學原理[M]. 陳咸亨 譯.北京:科學出版社,1965.
[2]楊伯君. 量子光學基礎[M]. 北京:北京郵電大學出版社,1996.
[3]朗道,栗弗席茲. 量子力學(非相對論理論)[M]. 北京:人民教育出版社,1980.
[4]費恩曼,萊頓,桑茲. 費曼物理學講義 [M].李洪芳 等譯. 上海:上海科學技術出版社,2005.
[5]戴巖偉. 淺談量子力學中算符運算的多種求法[J].安徽師范學院學報,2005(2):31-32.
[6]山卡(美). 量子力學原理[M]. 北京:世界圖書出版社北京公司,2007.
[7]喀興林. 高等量子力學[M]. 北京:高等教育出版社,1999.
[8]吳兆顏. 高等量子力學[M]. 長春:吉林大學出版社,2008.
[編輯] 洪云飛
10.3969/j.issn.1673-1409.2011.09.005
O413
A
1673-1409(2011)09-0010-03

