一類帶參數的四階兩點邊值問題正解的存在性

黃永峰

(昌吉學院數學系，新疆 昌吉 831100)

一類帶參數的四階兩點邊值問題正解的存在性

黃永峰

(昌吉學院數學系，新疆 昌吉 831100)

通過應用錐上的不動點定理討論了一類帶2個參數的四階兩點邊值問題正解的存在性,給出了正解存在的充分條件。

四階邊值問題；錐；正解；存在性

(1)

1 預備知識

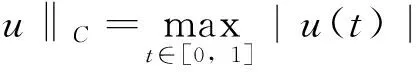
設Gi(t,s)為線性邊值問題：

-u″(t)+μiu(t)=0t∈[0,1]u′(0)=u′(1)=0i=1,2

由此可知，邊值問題在C4[0,1]中的解等價于方程:

(2)

(i)Gi(t,s)>0,t,s∈(0,1);

(ii)Gi(t,s)≤CiGi(t,s),t,s∈(0,1);

(iii)Gi(t,s)≥δiGi(t,t)Gi(s,s),t,s∈(0,1)。

引理2當f∈C([0,1]×(0,∞),[0,∞))時,邊值問題(1)的解滿足：

證明由方程(2)及引理1中(ii)知：

(3)

再由引理1中(iii)，式(3)可得：

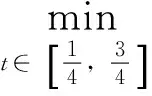
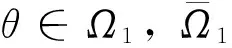
(i)‖Ax‖≤‖x‖,?x∈P∩?Ω1;‖Ax‖≥‖x‖,?x∈P∩?Ω2;

(ii)‖Ax‖≤‖x‖,?x∈P∩?Ω2;‖Ax‖≥‖x‖,?x∈P∩?Ω1，

2 主要結論

定理1如果f(t,u),ξ,η滿足基本的假設條件,同時存在2個不同的正常數λ、η,使得:

f(t,u)≤λC(t,u)∈[0,1]×[0,λ]

(4)

(5)

同時成立,則邊值問題(1)至少有一個解u,且‖u‖在λ，η之間。其中:

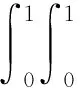
證明邊值問題(1)等價于積分方程:

(6)

不失一般性，不妨設λ<η。取Ω1={u∈C[0,1]:‖u‖<λ}，則當u∈K∩?Ω1時,由式(6)、引理1中(ii)及式(4)得：

故有‖Au‖≤‖u‖,u∈K∩?Ω1。

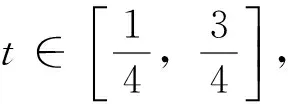
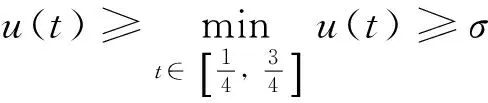
故有‖Au‖≤‖u‖,u∈K∩?Ω2。

由上面定理很容易得到下面的一些結果，其證明只是簡單地用到定理的結論。下面這些結果均設f(t,u),ξ,η滿足基本假設條件，記：

推論1C,D同定理1，若以下條件之一滿足:

則邊值問題(1)至少有一個正解。

推論2C,D同定理,若以下條件同時滿足:

(i)f0=L1∈[0,C)，f∞=L4∈[0,C)；

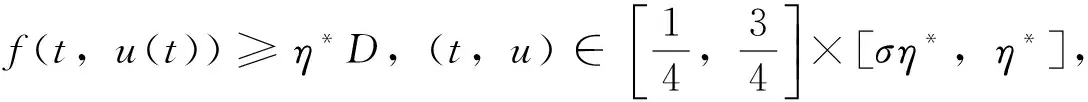
則邊值問題(1)至少有兩個正解u1和u2,且滿足0<‖u1‖<η*<‖u2‖。

推論3C,D同定理,若以下條件同時滿足:

(ii)存在λ*>0 使得f(t,u(t))≤λ*C,(t,u)∈[0,1]×[0,λ*]，

則邊值問題(1)至少有2個正解u1和u2,且滿足0<‖u1‖<λ*<‖u2‖。

[1]Ma R Y, Wang H Y. On the existence of positive solutions of fourth-order ordinary differential equations[J]. Applications of Analysia,1995,59:225-231.

[2] 馬如云. 四階邊值問題的多個正解[J]. 西北師范大學學報(自然科學版), 1997,33(2):1-5.

[3] Li Y X. Positive solutions of fourth-order boundary value problem with two parameters[J]. Journal of Mathematical Analysis and Applications, 2003,281:477-484.

[4] Bai Z B, Wang H Y. On positive soulutions of some nonlinear fourth-order beam equations[J]. Journal of Mathematical Analysis and Applications, 2002,270:357-368.

[5] Liu B. Positive solutions of fourth-order boundary value problems[J]. Appl Math Comput,2004,148:407-420.

[6] 郭大鈞.非線性泛函分析[M].第2版.濟南:山東科學技術出版社,2001.

[編輯] 洪云飛

10.3969/j.issn.1673-1409.2011.09.001

O175.8

A

1673-1409(2011)09-0001-03