鋼材磁通量與應力關系的磁力學模型及試驗研究
熊二剛,王社良,趙均海,高志華,李波
(1.長安大學 建筑工程學院,陜西 西安710061;2.長安大學 舊橋檢測與加固技術交通行業重點實驗室,陜西 西安 710064; 3.西安建筑科技大學 土木工程學院,陜西 西安 710055)
由于鐵磁材料具有逆磁致伸縮效應,所以應力一直被認為是影響鐵磁材料磁特性的重要因素.當鐵磁材料受拉、壓應力作用時,其磁參數將發生變化,如磁導率、矯頑力、初始磁化率、可逆磁化率,有助于磁化的磁彈性作用以及殘余磁化強度.因此,使用這些效應來對滿足不同需求所設計的鐵磁鋼結構進行無損應力檢測是非常有意義的.
盡管國內外專家學者已將基于磁特性(如磁導率、矯頑場等)的磁性無損檢測技術應用于航空航天、機械和石油等行業,并且成功地檢測到了應力集中區、應變集中區和缺陷等[1-3].但是在土木工程領域[4-6],通過全磁通來檢測鋼結構構件(鋼材屬于鐵磁材料)的實時應力,并對其磁與力之間相關關系的研究卻少見報道.針對大跨鋼結構,因其構件都屬于鐵磁材料,并且其大多數構件都只是受單軸拉、壓應力作用,通過對構件的實時應力監測,就可以了解整個結構的安全狀況.本文根據磁化的應力敏感這一特性,提出了鋼材一種基于能量的磁通量變化與應力關系的磁力學模型.
1 鐵磁材料基于能量的磁力學模型
在外磁場作用下,鐵磁材料內磁疇的磁矢會向使系統能量為最小的幾個方向偏轉,因而各磁疇的磁矢取向都不相同,總自由能E包括外磁場的磁化能EH、自磁化能Ed(退磁能)、磁晶各向異性能EK、磁致伸縮能Eσ(磁彈性能)和交換自由能Ee等[1-4],即
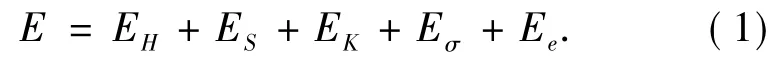
其中:
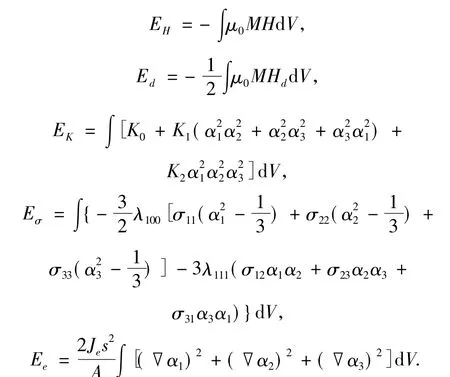
式中:M為磁化強度,H為外磁場,Hd為材料表面及體內磁極子磁場,K1、K2為磁晶各向異性常數,α1、α2、α3為磁疇磁矢與坐標軸之方向余弦,λ100、λ111為晶向的飽和磁致伸縮系數,Je為交換積分,s為原子自旋向量,A為晶格常數.
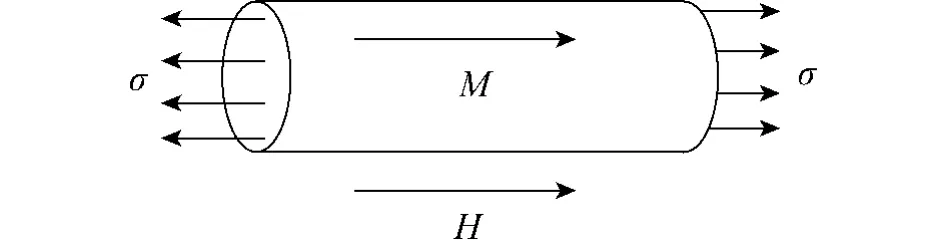
圖1 圓形試件Fig.1 Round specimens
以如圖1所示的鐵磁材料模型試件為研究對象,其截面為圓形,截面積為S,體積為V.
設試件的磁感應強度為B,根據文獻[5-7]可知
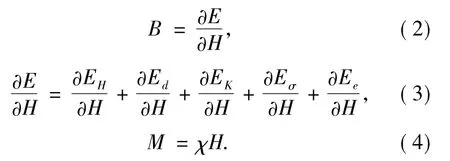
式中,χ為磁化率.
因為M和H都是均勻分布的,所以
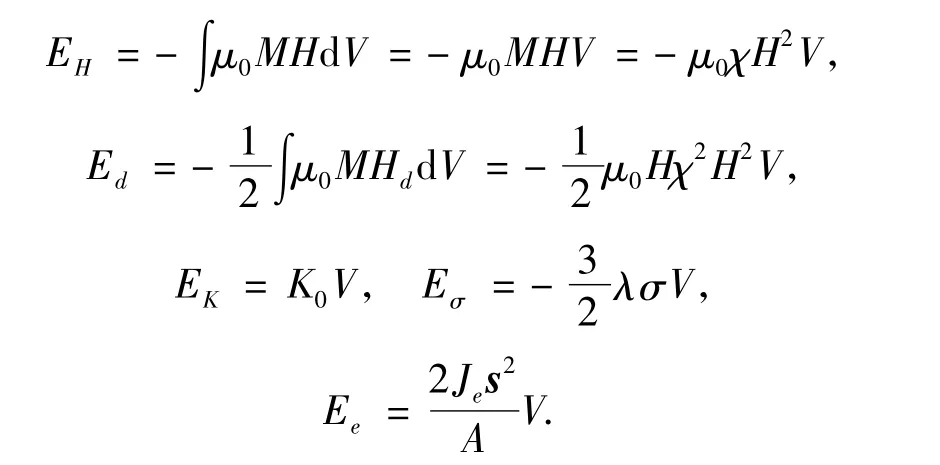
式中:λ為磁致伸縮系數;N為退磁系數,只與試件的形狀有關[8-9].
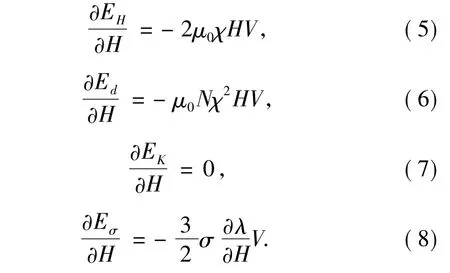
根據文獻[10-11]可知

式中,α為耦合系數.
根據文獻[12-13]可知:
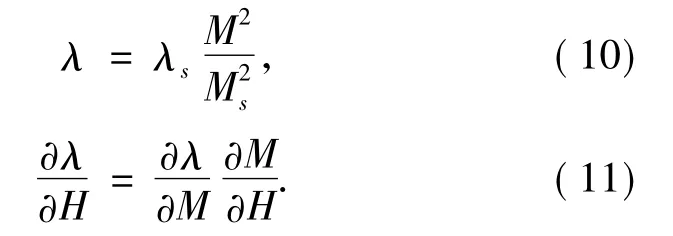
將式(10)代入式(11)可得
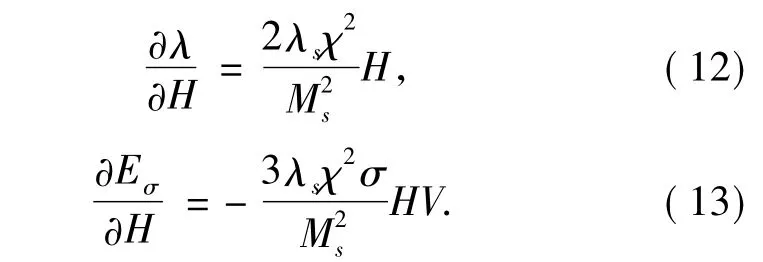
所以
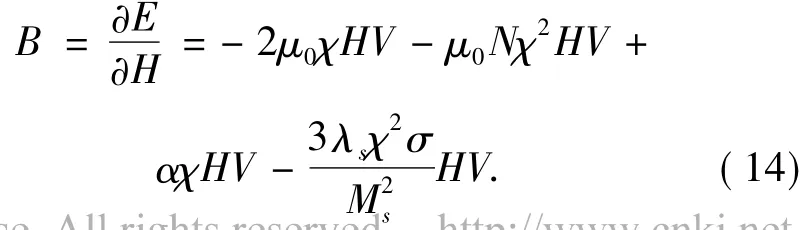
當試件同時受到磁場H和應力場σ作用時,可以等價于先給試件加磁場H,待磁場作用完畢后,再給試件加應力場σ,也可以等價于先給試件加應力場σ,待應力場作用完畢后,再給試件加磁場H.
對于本文中的模型試件,可以先給試件加磁場H,此時試件即被磁化,其磁化強度為M,磁化率為χ.再給試件加應力場σ,這時應力對磁化強度和磁化率的貢獻可以通過假象的磁場?Eσ/?H來反映,即在H和σ(?Eσ/?H)的共同作用時,試件的磁化強度和磁化率將改變.因此,在式(14)中,對于磁場H產生的磁化率χ,可以不考慮應力場σ的作用,而把應力場σ的影響反映在假象磁場?Eσ/?H的作用中.此外,當之前作用的磁場H給定時,?EH/?H、?Ed/?H、?Ee/?H為定值并且與后加應力場σ無關.所以,磁感應強度的增量與應力之間的關系如下:

式中,K為常數.磁通量的變化量與應力也存在如下關系:
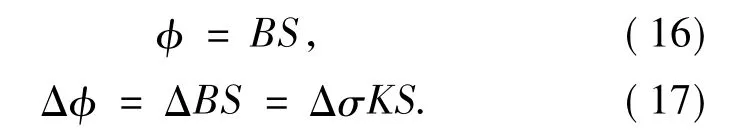
式中Δφ為磁通量增量,ΔΒ為磁感應強度增量,Δσ為應力增量.從式(17)可以看出,對于給定的磁場,磁通量增量與應力增量之間存在著線性關系.
2 試驗及討論
模型試件采用Q235鋼材制作,直徑分別為4、16 mm,模型試件的形狀和尺寸等詳見表1.模型試件及夾頭如圖2、3所示.采用NIM-2000 HF磁力耦合試驗機,使用小電源和磁場手動加載,得到磁通量增量與拉、壓應力的試驗結果[14],如圖4、5所示.
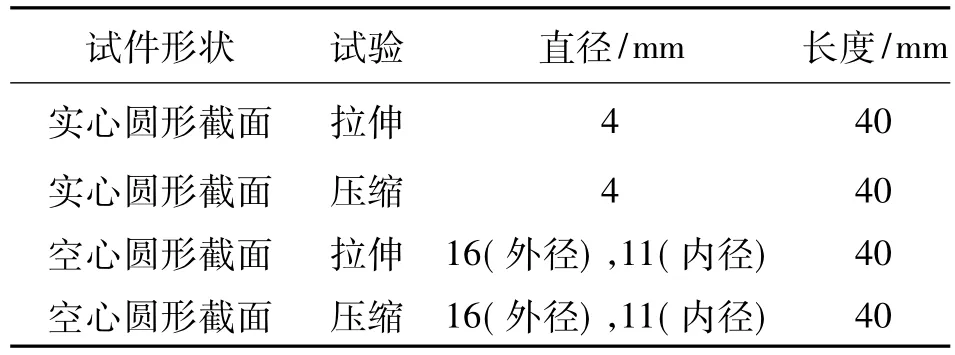
表1 試件的形狀及尺寸Table 1 Shapes and sizes of specimens
從圖4、5中可以看出,試驗結果與計算結果吻合較好.同時,4 mm直徑實心圓鋼模型試件和16 mm直徑空心鋼管模型試件磁通量的變化量均隨著其拉應力的增大而增大,均隨其壓應力的增大而減小,并且與外加應力呈較好的線性關系.也就是說,磁通量隨拉應力的增大而線性增大,隨壓應力的增大而線性減小,這為全磁通應力檢測技術提供了方便.

圖2 4 mm直徑實心圓鋼模型試件及夾頭Fig.2 4 mm diameter solid steel model specimens and chucks

圖3 16 mm直徑實心圓鋼模型試件及夾頭Fig.3 16 mm diameter steel tubular model specimens and chucks
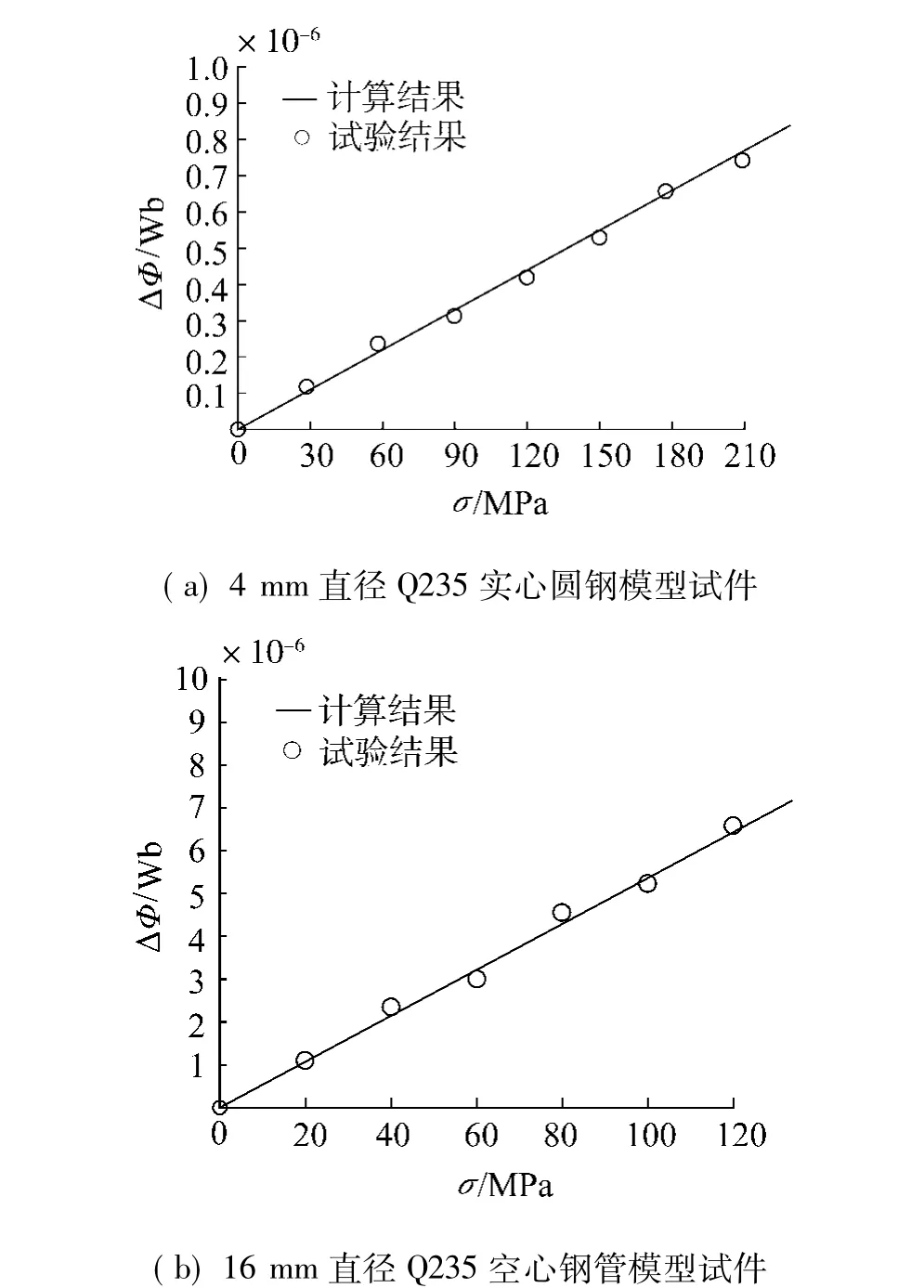
圖4 拉應力與磁通量變化量的關系Fig.4 Tensile stress versus the change in the magnetic flux
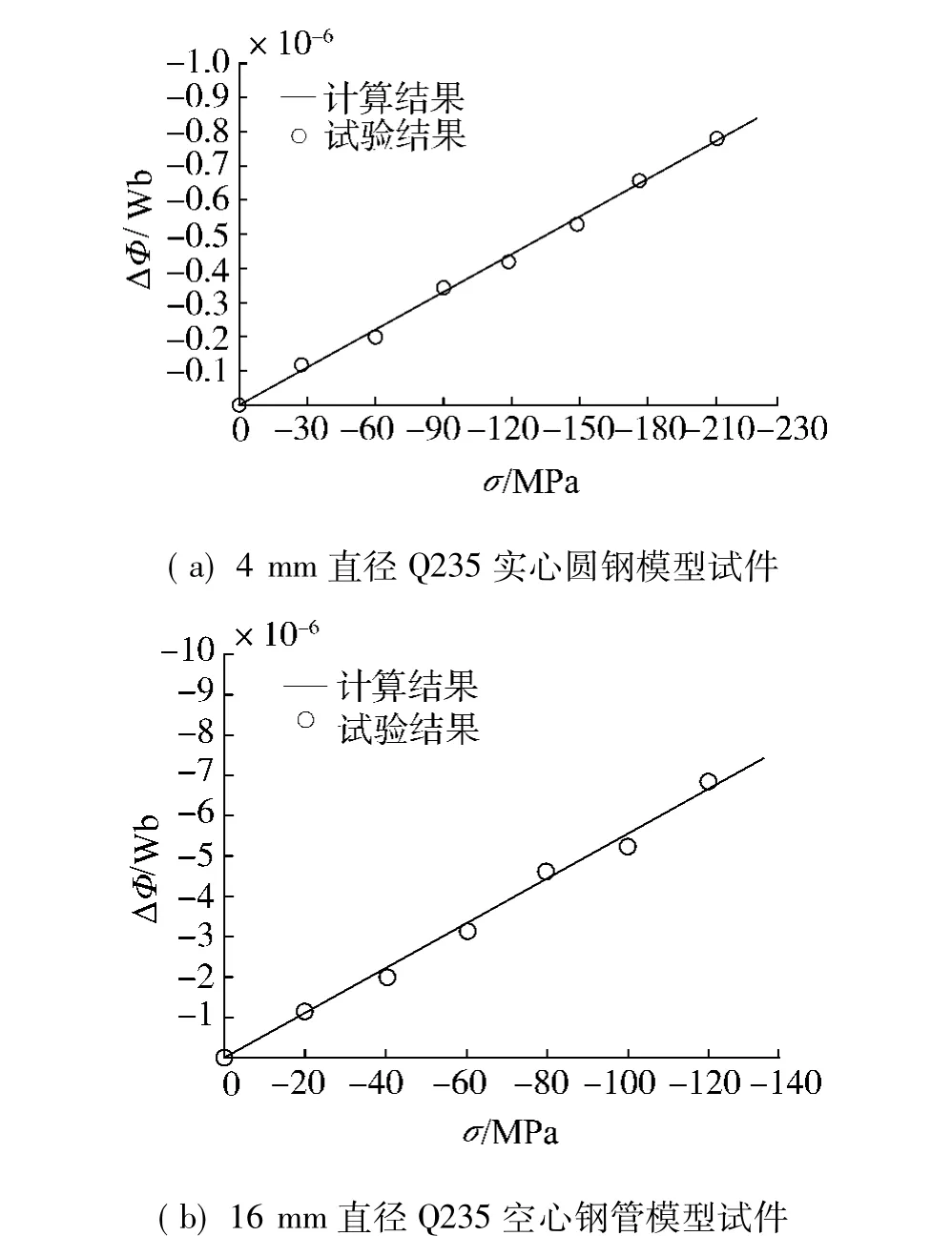
圖5 壓應力與磁通量變化量的關系Fig.5 Compressive stress versus the change in the magnetic flux
3 結論
1)根據鐵磁材料的磁化強度對外加應力敏感這一特性,從微磁能量原理出發,建立了鋼材磁通量增量與其應力增量的關系方程.該關系可以反映鐵磁材料磁力本構關系的主要特征,據此可以作為磁力耦合傳感器的基礎.
2)試驗結果表明,式(17)計算的結果與試驗結果吻合較好,證明了該公式的正確性.
3)不同直徑實心圓鋼和空心鋼管模型試件在外加磁場和外加應力的共同作用下,其磁通量隨著拉應力的增大而線性增大,但隨壓應力的增大而線性減小,所得試驗數據和所提磁力學本構模型即奠定了鋼結構全磁通應力無損檢測理論的基礎,具有較高的理論意義和實用價值.
[1]BUTTLE D J,DALZELL W,THAYER P J.Nondestructive residual stress measurement in rail heads and rolling contact fatigue[J].Insight,2002,44(6):364-368.
[2]JILES D C.Introduction to magnetism and magnetic materials[M].2nd ed.Lodon:Chapman and Hall,1998:280-297.
[3]GEOFFROY O,PORTESEIL J L.Scaling properties of irreversible magnetization and their conesquences on the macroscopic behavior of soft materials[J].J Magn Magn Mater,1994,133(1-3):1-5.
[4]姜壽亭,李衛.凝聚態磁性物理[M].北京:科學出版社,2003:285-289.
JIANG Shouting,LI Wei.Magnetic physics of the condensed matter[M].Beijing:Science Press,2003:285-289.
[5]BESBES M,REN Z,RAZEK A.Finite element analysis of magneto-mechanical coupled phenomena in magnetostrictive materials[J].IEEE Trans Magn,1996,32(3):1058-1061.
[6]KALETA J,TUMANSKI S,ZEBRACKE J.Magnetoresistors as a tool for investigating the mechanical properties of ferromagnetic materials[J].J Magn Magn Mater,1996,160:199-200.
[7]羅健豪.無損殘余應力測量及其新技術[J].力學與實踐,2003,25(4):7-11.
LUO Jianhao.Non-destructive evaluation of residual stress[J].Mechanics and Engineering,2003,25(4):7-11.
[8]GROS L,REYNE G,BODY C,MEUNIER G.Strong coupling magnetomechanical methods applied to model heavy magnetostrictive actuators[J].IEEE Trans Magn,1998,34 (5):3150-3153.
[9]REYNE G,SABONNADIERE J,COULOMB J,et al.A survey of the main aspects of magnetic forces and mechanical behavior of ferromagnetic materials under magnetization[J].IEEE Trans Magn,1987,23(5):3765-3767.
[10]BESBES M,REN Z,RAZEK A.Finite element analysis of magneto-mechanical coupled phenomena in magnetostrictive materials[J].IEEE Trans Magn,1996,32(3): 1058-1061.
[11]MELIKHOV Y,JILES D C,TOMáS I,et al.Investigation of sensitivity of Preisach analysis for nondestructive testing[J].IEEE Trans Magn,2001,37(6):3907-3912.
[12]CHEN Y,KRIEGERMEIER-SUTTON B K,SNYDER J E,DENNIS K W,et al.Magnetomechanical effects under torsional strain in iron,cobalt and nickel[J].J Magn Magn Mater,2001,236(1-2):131-138.
[13]CULLITY B D.Introduction to magnetic materials[M].Addison Wesley,Reading,MA,1972:557-564.
[14]熊二剛.基于磁力效應的鋼結構全磁通應力檢測技術的理論和試驗研究[D].西安:西安建筑科技大學,2008:128-136.
XIONG Ergang.Theoretical and experimental research on total magnetic flux stress testing technique for steel structure based on the magnetomechannical effect[D].Xi'an:Xi'an U-niversity of Architecture&Technology,2008:128-136.

