利用平面GPS高程擬合法求均值的討論

張想平

(蘭州市城市建設設計院，甘肅蘭州 730030)

利用平面GPS高程擬合法求均值的討論

張想平?

(蘭州市城市建設設計院，甘肅蘭州 730030)

主要討論了利用平面GPS高程擬合法求均值的原理和方法，并引用實例對擬合高程與四等水準高程進行了比較，就比較結果進行了討論。

高程擬合；平面；求均值

1 前 言

近年來，GPS技術在測繪領域得到了廣泛的應用。特別是在控制測量方面，由于其平面測繪成果精度高、觀測方法簡便、兩點之間不需要通視和全天候觀測等優點而成為現代測繪技術的主要手段。我們知道，利用GPS定位技術獲取的測量成果經過三維約束平差后，我們能夠獲取得到在當地坐標系下精度較高的點位平面坐標值。但是，GPS觀測所得到的是大地高，大地高也稱為橢球高，是以參考橢球面為基準面的高程系統。某點的大地高是該點到通過該點的參考橢球的法線與參考橢球面的交點間的距離，是一個純幾何量，不具有物理意義。同一個點，在不同的基準下，具有不同的大地高。而在實際的應用中，我們采用的是正常高。正常高是以似大地水準面為基準的高程系統。某點的正常高是該點到通過該點的鉛垂線與似大地水準面的交點之間的距離。大地高與正常高之間有如下幾何關系:H＝Hγ＋ζ。ζ為高程異常。為了確定出正常高，需要求出高程異常數據。求解高程異常數據的方法通常有等值線圖法、地球模型法、高程擬合法等多種方法。高程擬合法是比較常用的GPS高程求解方法。

2 高程擬合法基本原理

所謂高程擬合法就是利用在范圍不大的區域中，高程異常具有一定的幾何相關性這一原理，采用數學方法，求解正常高或高程異常。利用高程擬合法求解高程異常通常有以下三種方法。

(1)常數法，也叫零次多項式法:ζ＝a0

(2)平面擬合法，也叫一次多項式法:

(3)曲面擬合法，也叫二次多項式法:

利用公共點上GPS測定的大地高和水準測量測定的正常高計算出該點上的高程異常ζ，存在一個這樣的公共點，就可以依據上式列出一個方程:

通過最小二乘法可以求解出多項式的系數:

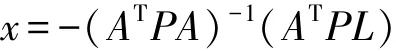
其中:P為權陣，它可以根據水準高程和GPS所測得的大地高的精度來加以確定。

3 選擇平面擬合法求均值的原理和優點

(1)選擇平面擬合法求均值的原理

選擇平面擬合法求均值就是在進行高程擬合的區域內，先選擇適當的3個或4個已知高程點確定進行高程擬合的平面，利用已知高程點的大地高和正常高求解出一組已知高程點的高程異常特征值ζ，根據ζ＝a0＋a1·dB＋a2·dL的原理，解算出式中的α0、α1、α2，在將α0、α1、α2代入ζ＝a0＋a1·dB＋a2·dL中，從而解算出高程擬合區域內其他GPS觀測點的高程異常值ζ，在利用正常高和大地高的關系式H＝Hγ＋ζ解算出高程擬合區域內其他GPS觀測點的一組正常高。(上述計算原理較為復雜，但在GPS觀測數據的解算軟件中都有高程擬合的步驟，可以任意的選擇高程擬合的方式，因此，利用GPS觀測數據的解算軟件進行高程擬合的解算十分簡單，只需在解算軟件中輸入已知高程點的高程而已。)利用同樣的辦法，進行高程擬合的區域內再選擇另外的3個或4個已知高程點(可以選擇一到兩個與前次相同的已知高程點，這樣可以減少所需要的已知高程點的數量。)確定進行高程擬合的另一個擬合平面，從而解算出高程擬合區域內另外一組GPS觀測點的正常高。諸如此類，我們可以利用高程擬合區域內所有的已知高程點解算出高程擬合區域內好幾組GPS觀測點的正常高，通過比較同一GPS觀測點的幾組正常高值，剔除掉同一GPS觀測點中較差比較大的一兩組正常高，再將剩余幾組GPS觀測點的正常高取平均值作為最終的高程擬合值。

(2)選擇平面擬合法求均值的優點

首先，我們知道，GPS高程擬合的方法是一種純幾何的方法。因此，普通的高程擬合方法(尤其是選擇常數法)一般僅適用于高程異常變化較為平緩的地區(如平原地區)，其擬合的準確度可達到一分米以內。對于高程異常變化劇烈的地區(如山區)，其準確度有限，這主要是因為在這些地區，高程異常的已知點很難將高程異常的特征表示出來。而利用求均值法可以有效消除高程異常變化劇烈而帶來的高程異常不確定的問題。

其次，選擇合適的高程異常已知點的問題:所謂高程異常的已知點的高程異常值一般是通過水準測量測定正常高、通過GPS測量測定大地高后獲得的。在實際工作中，一般采用在水準點上布設GPS點或對GPS點進行水準聯測的方法來實現，為了獲得好的擬合結果要求采用數量盡量多的已知點，它們應均勻分布，并且最好能夠將整個GPS網包圍起來。由于常數擬合法的可靠性較低，我們一般不采用該方法。采用平面擬合法要確定3個參數，需要3個以上的已知點，最好每次擬合選用4個已知點，這樣我們就可以將兩個已知點選擇在高程擬合區域內的中間，兩個已知點選擇在高程擬合區域內的兩頭即保證了已知點的分布均勻，又能夠將整個GPS網包圍起來，更重要的是需要已知點高程點數不多，(6個已知點就可以選擇5種以上不同的擬合方案。)大大減少了GPS點進行水準聯測的工作量。而曲面擬合則不同，該方法要求確定6個參數，則需要6個以上的已知點，要保證已知點均勻分布且能夠將整個GPS網包圍起來，則已知點必須分布在整個擬合曲面內，這大幅度增加了GPS點進行水準聯測的工作量。

4 應用實例

(1)南山路是蘭州市政府規劃的鐵路以南的一條項重要道路，該路是蘭州市政府規劃的貫穿整個蘭州市的四條東西大通道之一，也是鐵路以南唯一一條東西走向的道路。該路的建成將對鐵路以南地區的經濟發展起到極大的帶動作用。去年9月，蘭州市城市建設設計院受蘭州市城投公司的委托，對該工程布置了大型的GPS控制網。該控制網東西向長約35 km，南北向長約0.8 km，最大高差100 m左右。筆者就該控制網利用部分已知水準點應用平面擬合法求均值的方法進行了擬合，擬合時每次選用分布在測區東面的N1、N2、N3三個已知點中的兩個點、分布在測區中間的已知點N6、分布在測區西面的已知點N17或N19四點構成擬合平面并用南方GPS平差軟件進行數據解算，然后用Excel電子表格格式導出解算結果，最后取5次解算結果的均值作為高程擬合的最終結果，結果如表1所示。

蘭州市南山路工程GPS高程擬合成果表 表1

備注:表中每列粗體字為本次擬合參與解算高程點。

(2)彭家坪地區四條道路工程:蘭州市彭家坪地區是蘭州市政府新批準的高新開發區，是未來蘭州市城市規劃的第八城市組團，其基礎設施建設特別是城市道路的建設，對該地區的經濟發展起到極大的帶動作用。彭家坪地區四條道路工程正是為了適應這一形勢的發展而啟動的。去年8月，我們對該工程布置了一個小型的GPS控制網和水準網。筆者就該控制網利用已知水準點應用平面擬合法求均值的方法進行了擬合，并就擬合結果和四等水準結果進行了比較，結果如表2所示。

蘭州市彭家坪路網工程GPS高程擬合成果表 表2

5 結 論

通過以上兩表的比較可以發現，筆者只選擇了5種不同的擬合方案，而且每個工程只有6個或7個已知水準點參與擬合，應用平面擬合法求均值的方法進行高程擬合，絕大部分點的擬合高程與四等水準高程的較差在±30 mm左右，甚至有許多點的較差達到了10 mm以下，只有一個點的擬合高程與四等水準高程的較差在59 mm左右，如果選擇的擬合方案更多些，其精度會更高些。我們還發現，就單次擬合高程而言，絕大部分點的擬合高程與四等水準高程的較差是個不確定值，總是在四等水準高程左右擺動，這充分說明，應用平面擬合法求均值的方法進行高程擬合，能夠很好消除高程異常變化劇烈而引起高程異常不確定所帶來的誤差，而且選擇的擬合方案越多，其效果越明顯。這說明，如果高程擬合的區域不大，點位選擇適當，高程擬合方案較多(10種左右)，應用平面擬合法求均值的結果完全可以達到四等水準的水平。

[1] 魏二虎，黃勁松編.GPS測量操作與數據處理.武漢:武漢大學出版社，2004

[2] 北京合眾合拓普科技發展有限公司.TOPCON/JAVAD GPS測量系統工程測圖放樣軟件操作手冊.

[3] CJJ73_97.全球定位系統城市測量技術規程.

A Discussion of Converting a GPS Height Into a Normal Height by Planes and Averaging

Zhang XiangPing
(Lanzhou Urban Construction Design Institute，Lanzhou 730030，China)

The attention is concentrated on the principles ang methods of converting a GPS height into a normal height by planes and averaging，then compare the consequence with converting a GPS height into a normal height and four equivalent level height by examples.

converting a GPS height into a normal height；planes；averaging

1672－8262(2011)01－73－03

P228

B

2010—03—17

張想平(1974—)，男，工程師，從事工程測量工作。