Excel在GM(1，1)沉降預測數據處理中的應用

黃維騰

(茂名市粵能電力股份有限公司設計院，廣東茂名 525000)

Excel在GM(1，1)沉降預測數據處理中的應用

黃維騰?

(茂名市粵能電力股份有限公司設計院，廣東茂名 525000)

GM(1，1)模型在沉降預測中已經廣泛應用，然而其計算過程復雜，在數據量較多的情況下計算量很大。本文以某沉降監測數據為例，提出利用Excel進行數據處理的方法，過程簡單，結果準確，極大方便了計算工作。

Excel；GM(1，1)；沉降預測；數據處理

1 前 言

隨著現代化進程的不斷加快，城市各類高層建筑日益增多。由于建筑物的增高，荷載的增加，在地基基礎和上部結構的共同作用下，建筑物可能發生不均勻沉降，輕者將使建筑物產生傾斜或裂縫，影響正常使用，重者將危及建筑物的安全，因此，必須對其進行沉降觀測。

高層建筑沉降監測的目的不僅僅是觀測其沉降值，更為重要的是根據已觀測的量值，通過建立一定的模型來預測其在未來某一時刻的可能沉降值，進而分析其安全性，將可能的損失消除在萌芽狀態或最大限度地減輕損失。沉降預測有回歸分析法、確定函數法、時序分析法等，但這些方法通常要求有大量樣本，而且要求具有典型的概率分布，這在實際工作中往往難以滿足。沉降預測中既包含已知信息，又有未知信息而且處于變化之中，這樣預測沉降量未來變化的問題，實質上可以看作一個灰色問題[1，2]。

2 GM(1，1)預測模型簡介

GM(1，1)模型是灰色理論中最常用的模型之一。它的建模是對生成數列的建模，它對原始數據沒有大樣本的要求，只要原始數列有4個以上的數據就可以通過變換來建立模型。目前GM(1，1)模型在建筑物沉降預測中有著廣泛的應用，并取得了良好的效果[3，4]。

GM(1，1)計算過程如下:

(2)利用此序列生成緊鄰均值序列z(1)(k)為

(3)建立灰色GM(1，1)模型的一級白化微分方程

(4)灰色GM(1，1)模型參數列A＝[a，b]T的最小二乘估計為

將計算求得的參數a，b帶入式(1)中求微分方程，取x(1)(0)＝x(0)(0)，可得到灰色GM(1，1)預測模型為:

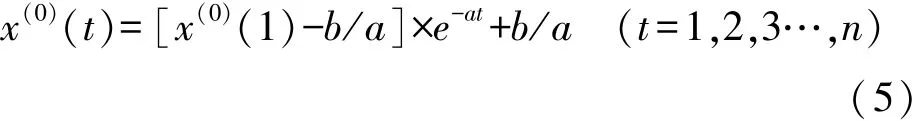
(5)對此式再做一階累減還原計算得到原始序列x(0)的灰色GM(1，1)預測模型為:

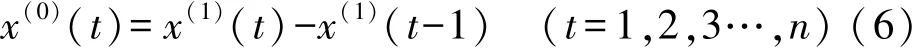
3 基于Excel的GM(1，1)數據處理[5]

3.1 數據準備

某高層建筑沉降觀測要求每月監測一次，共計觀測16次，取得了豐富的數據。為了便于計算，選擇一個有代表性的沉降觀測點說明，數據如圖1所示。

在數據錄入后，在C2單元格中輸入公式“＝B2”；在C3單元格中輸入公式“＝B3＋C2”，回車。將光標指向C3單元格的右下角，待其變成細小的黑十字后雙擊或下拉至C17，即可得到全部累加生成結果，如圖1所示。

在D3單元格中輸入計算公式“＝－AVERAGE (C2:C3)”，回車，將光標指向D3單元格的右下角，待其變成細黑十字后雙擊或者下拉至D17，即可得到全部移動平均的負值，如圖1所示。

在E3－E17添加一列數字1，這些1與移動平均的負值并排，構成用于估計參數的矩陣B。然后將原始數據從B3－B17復制并粘貼到B矩陣的右側，如圖1所示，這樣就完成了數據預備工作。

圖1 數據預備圖

3.2 最小二乘運算

(1)計算矩陣BTB及其逆矩陣(BTB)－1。選定一個2?2的單元格區域，如G3:H4，然后借助Excel的矩陣乘法函數mmult和矩陣轉置函數transpose，輸入計算公式

同時按住Ctrl＋Shift鍵，回車，即可得到BTB的計算結果，如圖2所示。

選定一個2?2的單元格區域，如G7:H8，借助Excel的矩陣求逆函數minverse，輸入計算公式:

同時按住Ctrl＋Shift鍵，回車，即可得到(BTB)－1的計算結果，如圖2所示。

(2)計算向量BTY。選定一個2?1單元格區域，如G11:G12，然后輸入計算公式:

同時按住Ctrl＋Shift鍵，回車，即可得到BTY的計算結果，如圖2所示。

(3)計算向量(BTB)－1BTY。選定一個2?1的單元格區域，如G15:G16，然后輸入計算公式:

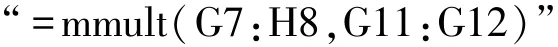
同時按住Ctrl＋Shift鍵，回車，即可得到(BTB)－1BTY的計算結果，如圖2所示。這個向量給出了GM (1，1)模型的參數估計值:

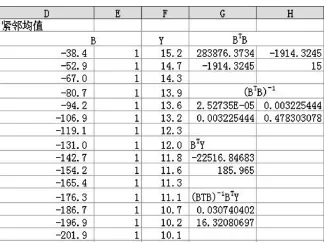
圖2 參數計算圖

3.3 建設模型

將計算得到的參數估計結果賦予GM(1，1)模型即可。

3.4 預測與檢驗

(1)重新整理數據，將觀測時間變為從零開始的時序，并輸入表格中，同時將參數復制到數據附近，如圖3所示。

(2)計算累計數據的預測值。根據GM(1，1)模型及參數，在D2單元格中輸入計算公式:

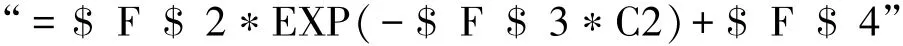
然后將鼠標光標指向單元格D2的右下角，待其變成細黑十字，雙擊或下拉，即可得到累加數據預測值的計算結果，如圖3所示。如果將時序繼續延伸，即可繼續預測。

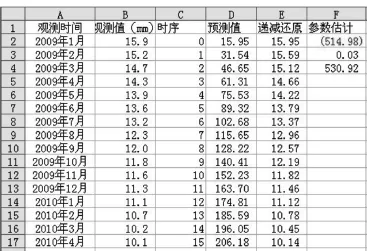
圖3 預測結果圖

(3)累加數據預測值的遞減還原。在E2單元格中輸入計算公式“＝D2”，回車；在E3單元格中輸入“＝D3－D2”，然后將鼠標光標指向單元格E3的右下角，待其變成細黑十字，雙擊或下拉，即可得到累加數據預測值的遞減還原結果，如圖3所示。

(4)計算絕對誤差與相對誤差。

利用Excel計算絕對誤差與相對誤差過程比較簡單，本文不再敘述，計算結果，如圖4所示。

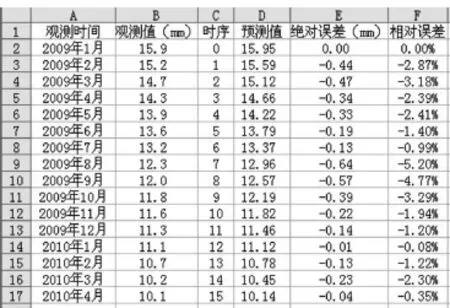
圖4 絕對誤差與相對誤差計算圖

4 Excel在數據處理中的優勢

(1)數據處理方便

利用Excel可以很方便的準備整理原始數據，且整理后的數據能夠直接進行計算。

(2)計算快捷

在GM(1，1)模型中參數運算中需要最小二乘運算，計算量很大，利用Excel的矩陣乘法函數、矩陣轉置函數、矩陣求逆函數可以快速的得到計算結果，且數據準確，無人為計算誤差。

(3)可以方便的檢驗結果

可以直接利用Excel的計算結果進行檢驗，計算出絕對誤差與相對誤差。

5 結 論

利用GM(1，1)模型進行沉降預測數據量較大，使用傳統方法進行計算費時費力且容易出錯，利用軟件編程計算對普通工作者有一定的難度，利用Excel軟件進行計算可以方便地進行數據整理，借助Excel函數計算快捷易用，并可方便地進行誤差檢核，在實際工作中有一定的應用價值。

[1] 鄧聚龍.灰色系統基本方法[M].武漢:華中理工大學出版社，1987

[2] 李日云，王利，張雙成.灰色預測模型在高層建筑物沉降預測中的應用研究[J].地球科學與環境學報，2005，27 (1):84～87

[3] 何濤，劉玉財，羊遠新.機場沉降監測數據處理的探討[J].城市勘測，2009(4):134～137

[4] 馮錦明，李炳芳.灰色預測模型在建筑物沉降監測中的應用[J].地礦測繪，2008，24(2):7～9

[5] 陳彥光.基于Excel的地理數據分析[M].北京:科學出版社，2010

Application of Excel to the Data Processing in the GM(1，1) Settlement Predication

Huang WeiTeng
(Maoming Yueneng Electrlc Power Co.，Ltd.Maoming 525000，China)

GM(1，1)model has widely used in the settlement predication.As its complex calculating process，the amount of calcuation is very great under the condation of a large quantity of data.Taking an settlement monitoring data as an example，this article puts forward the mean of data handling by Excel.The result shows that it has the advantages of simplicity and accuracy and it is a great convenience for calculation.This mean also has a certain application value in the GM(1，1)settlement predication.

Excel；GM(1，1)；Settlement Predication；Data Handling

1672－8262(2011)01－113－03

P209

B

2010—07—12

黃維騰(1979—)，男，工程師，主要從事工程測量、電力測量工作。