中間法對建筑物懸挑結構下沉監測及精度分析

張德強，余代俊，蒲朝旭

(成都理工大學地球科學學院，四川成都 610059)

中間法對建筑物懸挑結構下沉監測及精度分析

張德強?，余代俊，蒲朝旭

(成都理工大學地球科學學院，四川成都 610059)

用全站儀中間法代替三、四等水準測量已基本得到業內人士的認同，有著比較完善的理論支撐和實踐論證，但在施測環境不能滿足中間法要求的一般條件下(如儀器置中)，將其用于建筑物懸挑結構下沉監測的研究較少。本文通過對某高樓樓頂高程點采取精密水準測量和中間法高程測量兩種方法進行高程傳遞的對比，論證了全站儀中間法在建筑物懸挑結構下沉監測中的應用的可行性，并分析了其適用條件。

全站儀中間法；精密水準測量；懸挑結構

1 引 言

水準測量和三角高程測量由于原理的不同和儀器精度的局限，二者在精度上始終存在著一定的差距，但是隨著全站儀距離測量和角度測量精度的提高，用全站儀中間法替代三、四等水準測量已得到業內人士的普遍認同。實踐證明，在滿足一定的條件下采用中間法替代高等級的水準測量是切實可行的，而其大大提高作業效率的作用也是顯而易見的。但是，當需要用全站儀在場地有限的高層建筑工地工作環境條件下近于垂直地傳遞高程時，能否通過中間法觀測程序和觀測方法的設計，以達到滿意的高程測量精度，這方面的研究具有一定的工程意義。

本文分別采用精密水準測量和全站儀中間法對成都理工大學第6教學樓樓頂高程點進行高程傳遞實驗，對用全站儀中間法傳遞高程進行了設計和實驗驗證，并對實驗精度進行了分析，從而為建筑物懸挑結構下沉監測提供了一種實用的方法。通過本實驗得到的可靠結論，擬將該方法用于本市類似條件下的某高層建筑物懸挑結構的下沉監測，并根據工地實際情況設計了觀測方案。

2 全站儀中間法測量原理及方案設計

2.1 中間法測量原理

圖1 中間法三角高程原理圖

如圖1所示，為了測定A、B之間的高差hAB，仿照水準測量原理，在A、B大致中間位置的P點架設全站儀，通過測距、測角，可間接求得A、B之間的高差hAB:

式中，S1、S2為前、后視斜距，α1、α2為前、后視豎直角，v1、v2為前、后視棱鏡高，K1、K2為前、后視觀測時的大氣折射系數，R為地球半徑，D1、D2為前、后水平距離。由式(1)可以看出，高差hAB已與儀器高無關了。若在同一測站位置進行高差返測，并且對調棱鏡(特制棱鏡桿，棱鏡高不變)，則有:

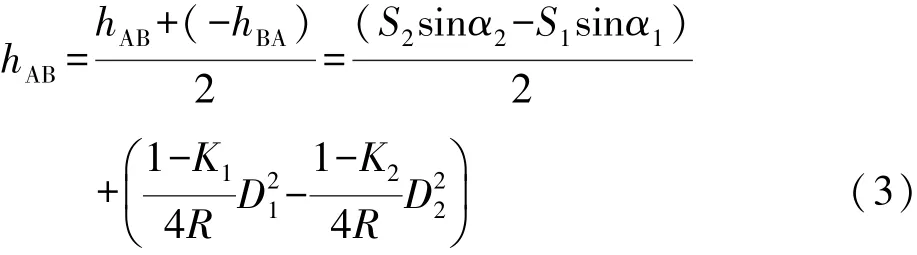
由上式可知，即使前后視棱鏡高不相等，也可在往返測高差平均值中抵消掉差值，采用這樣的中間法觀測程序，測定的高差也只與距離、豎直角及大氣折射系數有關，而與儀器高和棱鏡高完全無關[1]。

大氣折射系數K1和K2一般不相等，要精確地定出某一時間的變化值是不可能的，但在同一地點，短時間內值的變化很小[2]，在一天內，大氣折射系數一般在0.08～0.14之間變化，在前后視折射系數取極值的情況下，有人通過計算得出結論:由于大氣折射系數不同，若能保持前、后水平視距大致相等，則可基本消除球氣差對高差測量的影響值。前后視高差、視距及視距差越小，由大氣折射系數變化引起的高差誤差就越小，反之，則越大[3]。本實驗的觀測條件與其有所不同，即限制前后水平視距基本相等且不大于20 m，前視豎直角取α1＝0°～1°后視豎直角取α2＝70°～90°。因前視測線基本平行于地面而位于同密度大氣層中，測線基本不產生大氣折射，加之視距較短，大氣梯度對高差測量的影響可視為零；而后視測線基本垂直于地面，與不同密度的大氣層呈垂直關系，大氣折射對測線的影響將更多地表現為測線的傳播速度受到的影響，因此，由大氣折射對后視高差的影響也可忽略不計。地球曲率與大氣折射對高差測量的影響類似，在本實驗中可忽略式(3)等號右邊第二項的影響。

因此，在不考慮棱鏡高差和大氣折射及地球曲率影響的條件下，對式(3)進行簡化，舍棄大氣折射及地球曲率影響部分，經微分并由誤差傳播定律可導出在本實驗條件下的全站儀中間法高差中誤差公式:

2.2 高層建筑物懸挑結構三角高程測量實驗設計及精度分析

在此選擇成都理工大學12層樓高的第6教學樓作為高程傳遞實驗場所，利用點D60、S1、S2作為實驗觀測點，其中D60為第6教學樓前的強制對中觀測墩，S1、S2為布設在第6教學樓樓頂女兒墻上的強制對中器，各點位置分布如圖2所示，特制棱鏡桿實物如圖3所示，該棱鏡桿可直接旋入對中器中，旋入深度由限位圈限位而保持每次棱鏡高相同。為了觀測近于垂直的目標，需要在觀測過程中將目鏡換成彎管目鏡。

圖2 特制對中桿及棱鏡安裝組合實物圖

圖3 高程點平面分布圖

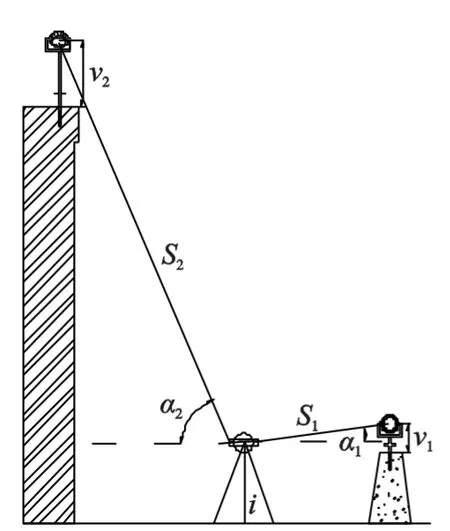
圖4 懸挑結構監測中間法測量實驗圖

圖5 懸挑結構監測實際施測設計圖

為了消除前后視棱鏡高不相同對高差測量的影響，可用交換目標棱鏡的方式來消除棱鏡高差誤差，為簡化精度估算公式，假設mα1＝mα2＝mα，由此可得:

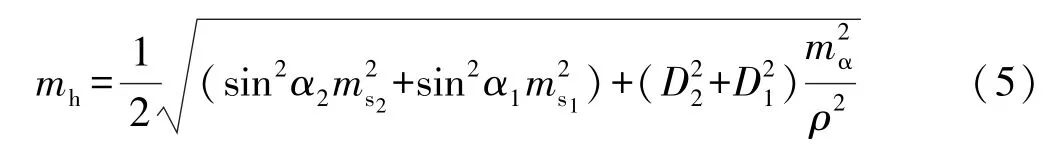
根據一般建筑施工現場的條件，地面目標點的位置不宜太遠，本設計取極限值20 m，則可由(5)式得知，高差精度受D1影響較小。鑒于架設在觀測墩上的后視棱鏡高度可以與全站儀儀高基本保持相同，且全站儀與建筑物懸挑結構上的前視目標棱鏡構成的前視視線近于垂直，在此分別取α1＝0°～1°，α2控制在70°～90°之間，假設前視目標與全站儀間的高差為100 m；視距D1控制在10 m～20 m之間；分別以標稱測角精度為0.5″和2″，測距精度為1 mm＋1 ppm和2 mm＋2 ppm的全站儀依式(5)計算高差精度，可得高差中誤差如表1和表2所示。

由表1、表2可見，當α1接近于0°且α2接近于90°時，對于兩種不同測角和測距精度的全站儀，在前后水平視距盡量小的情況下，測站高差中誤差主要受測距標稱精度的影響。由此可以進一步推證，在高層建筑物懸挑結構沉降觀測中，在儀器性能穩定的情況下，運用同一臺全站儀，滿足上述豎直角和前后視距限定條件下，采用三角高程測量方法觀測同一目標獲得的高程值精度主要由儀器測距精度決定，因此，用此法進行懸挑結構下沉監測時，各期觀測數據之差值可以作為沉降變化量。根據建筑變形測量規范(JGJB－2007)中的精度指標要求，選取以上標稱精度的全站儀采用中間法的高差精度理論計算值均可滿足三級精度要求[4]。

1.廣西與東盟國家貿易規模分析。“一帶一路”倡議提出之前，廣西憑借區位優勢與東盟國家建立一定的貿易合作關系，但總量上仍有很大發展空間。2012年，廣西與東盟國家實現進出口貿易116.36億美元，占全區進出口總額的43%。“一帶一路”倡議提出后，廣西與東盟國家進出口總額不斷上升（見圖1），平均增長速度為25%。雖然2016年外貿進出口總量縮減到177.42億美元，同比下降22.13%。但進入2017年后，與東盟進出口貿易回暖，僅上半年就實現進出口總額99.3億美元，同比增長16.34%。

全站儀(0.5″，1 mm＋1 ppm)測站高差中誤差 表1

全站儀(2″，2 mm＋2 ppm)測站高差中誤差 表2

3 測量方法試驗

3.1 精密水準測量實驗

測量選用Leica DNA03精密電子水準儀，嚴格按照精密水準測量模式，從地面高程點D60引測，沿第6教學樓B座樓梯間向上推至12層樓頂，測量S1、S2各高程點后，沿A座樓梯間向下返回至D60形成閉合路線，如圖6所示。由此推算出S1、S2各點高程，水準路線長度為0.614 km，閉合差為－0.4 mm，而其一等水準環線閉合差限差要求為±20.61385≈±1.57 mm，因此測量成果滿足一等水準測量精度要求，數據可靠[5]。

圖6 水準路線立面示意圖

3.2 中間法實驗

全站儀中間法實驗從D60引測，選用儀器為Leica TC402，按以下要求進行了施測；

(1)適位安置全站儀，經調整位置和高度后照準后視目標棱鏡中心，使地面水準點傳遞高程到樓頂時須保證0°≤α1≤1°，且70°≤α2≤90°，水平視距控制在20 m以內等條件滿足之后，輸入溫度、氣壓，然后再進行施測；

(2)觀測前旋下目鏡，裝上彎管目鏡，以觀測墩點為后視點，采用后(盤左)一后(盤右)一前(盤左)一前(盤右)測量程序，前、后視各觀測一測回；

(3)交換前視與后視兩點的棱鏡(特制棱鏡桿，各棱鏡高不變)；

(4)以樓頂點為后視點進行返測，取往返測高差平均值為最或是值。

3.3 成果對比

通過兩種測量方法，以D60假定高程為0.000 0 m，最終計算得到了S1、S2高程值，如表3所示。

兩種測量方法成果對比 表3

由上表可見，中間法與水準測量之間的高差較差基本與理論估算高差精度相當，由此可以推斷，在高層建筑物懸挑結構沉降監測中，選取上述條件非常適合進行監測，采用中間法產生的誤差基本上是由儀器的測距誤差引起。

4 結 論

通過對全站儀中間法的精度分析和實驗可知，在高層建筑物懸挑結構沉降觀測中，前后視豎直角無法保證相等的情況下，按照盡量控制水平距離在20 m以內，后視豎直角盡量保持0°，前視豎直角盡管近于90°的情況下，測定目標點高程，其獲得的高程值主要還是受儀器測距精度的影響，大氣折射系數對測距的影響可忽略不計。因此，在相似的觀測條件下，運用同一臺性能穩定的全站儀，且滿足上述豎直角和前后視距限定條件下，采用中間法觀測同一目標獲得的高程值只受儀器測距精度影響，其差值可以作為建筑物沉降量，其測站高差精度可達到建筑變形測量規范三級精度要求，因此，此法適用于高層建筑物懸挑結構下沉的監測。根據本實驗所得結論，鑒于本市某高層建筑物懸挑結構下沉觀測條件與本實驗觀測條件類似，擬將該方法用于此項目的下沉監測中，其施測設計見圖5所示，圖中儀器安置于建筑結構體上，如果沒有在結構體上安置儀器的條件，則后視點也需設置在結構體外。由于監測的是高差的變化量，因此，每期監測只要固定選用前視及后視的特制棱鏡桿，則可只進行往測而無需返測，從而提高工作效率。

[1] 余代俊.全站儀中間法替代二等水準測量的精度分析與實驗.測繪與空間地理信息，2006，29(5):117～120

[2] 許國輝.高精度EDM三角高程測量的研究[J].測繪通報，2002，(10):22～24

[3] 何習平.全站儀中間法與水準測量的精度比較.水電自動化與大壩監測，2004，28(4):37～39

[4] JGJB－2007.建筑物變形測量規范[S].

[5] GB12897－91.國家一、二等水準測量規范[S].

Subsidence Monitoring and Accuracy Analysis of the Building with a Cantilevered Structure Using Midway Method

Zhang DeQiang，Yu DaiJun，Pu ChaoXu
(Earth Sciences College，Chengdu University of Technology，Chengdu 610059，China)

The replacement of the third and the fourth grade leveling with Total Station Midway method has been recognized by the professionals in this industry.Though it has a more perfect theoretical support and practical arguments，there is little research on the application of Total Station Midway method to the building cantilever structure subsidence monitoring in the conditions of that the surveying environment with Midway method can not meet the general requirements (for example，the Total Station can’t be placed in the middle).This paper proofs the feasibility of the application of Total Station Midway method to the building cantilever structure subsidence monitoring and analyzes its application conditions，with the contrast to precise leveling on a tall building’s carry－over elevation experiment.

Total Station Midway method；precise leveling；cantilever structure

1672－8262(2011)01－133－04

P224.1，P258

B

2010—07—06

張德強(1981—)，男，碩士研究生，現就讀于成都理工大學地球科學學院攝影測量與遙感專業。