基于新陳代謝GM(1,1)模型的客車軸溫預測算法

曹寅冬

(武漢鐵路局 武昌客車車輛段,湖北武漢430064)

防止機車車輛燃軸和切軸事故,一直都是鐵路安全防范的重點工作之一。目前常用的滾動軸承故障診斷方法主要有3種,一是溫度診斷方法,二是振動診斷方法,三是聲學診斷方法。溫度診斷方法歷史悠久,應用廣泛。從20世紀70年代開始運用紅外線技術探測列車軸溫,到現在每列客車在每節車廂都安裝軸溫報警器[1],從單機監測到聯網監控,從人工抄軸報到IC卡記錄軸溫數據及TCDS無線網絡傳輸,溫度診斷方法仍在不斷地發展與完善。

紅外線軸溫探測系統預報軸承故障的準確率僅能達到30%—50%[2]。對于客車軸溫報警器,因為報警算法較為簡單,容易受到噪聲干擾、環境溫度等因素的影響,所以預報軸承故障的準確率也有待提高。特別是對于一些早期軸承故障,現有客車軸溫報警器的報警算法僅憑某一時刻軸溫是否超過預設值是難以發現的。譬如,2008年6月22日武漢鐵路局擔當的Z12次在運行途中被紅外線軸溫探測系統預報機后 18位軸溫強熱[3],經確認報警無誤,而車載軸溫報警器數據卻與實際軸溫存在較大出入,未能引起讓乘務人員足夠警覺。

客車軸溫報警器定點報警的計算公式是軸溫≥90℃;跟蹤報警的計算公式是軸溫 ≥環境溫度+45℃,可見其報警條件取決于某時刻軸溫和環境溫度的一元線性關系。然而,列車在運行中,軸溫受環境、車速、載重等諸多因素的影響,本身就具有隨機性和模糊性[4]。在現有條件下,很多因素無法測知,軸溫報警器只能采集軸溫和環境溫度,判別條件不充足。同時,由于列車非勻速運行,軸溫起起伏伏,加上軸溫報警器本身的測溫精度不高,如果不滿足報警條件將很難發現溫升處于45℃以下區間(譬如40℃～45℃)的軸承故障。軸承從產生故障到切軸,時間很難確定,最短可能幾分鐘。因此,改善軸溫報警器熱軸判別算法非常有必要。

闡述一種基于時間序列趨勢進行動態判定軸溫超高的方法,利用灰色系統理論建立新陳代謝GM模型預測軸溫變化,根據變化趨勢判斷軸溫是否超高,從而改善客車軸溫報警準確度。程序安裝在 TCDS系統的車載QNX主機上,不需改變現有硬件結構和報警模式。

1 灰色系統理論[5]

灰色系統理論是研究少數據不確定性的理論,簡稱灰理論或灰論(Grey Theory)。基于灰色系統理論的預測稱為灰色預測。作為灰預測的原始數據一般以時間序列的形式出現,可以少到只有4個數據。灰色預測方法以微分方程為工具,能夠準確地提取原始序列的內在變化規律,其預測過程其實是一個灰色過程的白化過程。

灰色預測方法的基本模型是灰色模型(GREY MODEL),簡稱GM。灰色模型是故障預測的一種有效模型,實際上是針對生成數列的建模。這種建模方式最大的優點在于只需較少的過程采樣數據,故計算量小,適合于實時應用。

最常用的灰色模型是GM(1,1)模型,由一個單變量的一階微分方程所構成:

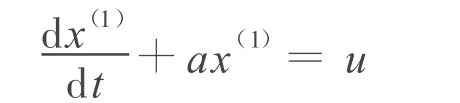
其中a和u為待辨識參數,稱a為發展系數,u為灰色輸入;x(1)是測量所得到的原始數列 x(0)的累加生成數列。

2 建立GM(1,1)模型的可行性

使用GM(1,1)模型進行建模前提條件是發展系數a的絕對值必須小于2,否則GM(1,1)模型無意義[6]。由于a是待辨識參數,只能在GM(1,1)模型建立之后進行判斷,為了能提前驗證GM(1,1)模型的有效性,一般用建模數列級比的大小和所屬區間,及其覆蓋來進行檢查。

對于序列 x=(x(1),x(2),…,x(n)),稱 σ(k)=為其級比。

σ(k)∈(0.135 3,7.389)?α∈(-2,+2)。即,當序列的級比在σ(k)∈(0.135 3,7.389)范圍內時,對序列進行GM(1,1)建模才有意義[6]。這被稱為“機理覆蓋”。如果想要建立精度較高的GM(1,1)模型,最好使用“數值覆蓋”,即σ(k)∈[]。

軸溫報警器每5.08 s發送一次數據,1 min大約能發送11次數據。假設我們以1 min為周期來觀察軸溫數據,在沒有干擾的情況下,軸溫具有很好的連續性,且變化平緩。根據1 min的數據個數,設定n=11,通過計算其數值覆蓋的范圍,可得

σ(k)∈ [0.846 48,1.181 36]

根據經驗推測,一般軸箱溫度在1℃/min之內變化,當增溫速度接近2℃/min時就可能是突發性燃軸的前奏[7]。通過歷年的軸溫存檔數據比對,相鄰兩個時刻(10 min之內)的溫度變化最高未超過8℃,即平均值為0.8℃/min,基本驗證了這個推測。

如果軸溫平穩變化,當溫度的絕對值偏小時,級比也會偏大,例如從1℃升高到2℃,溫升為1℃,級比為0.5,小于0.84大于0.135 3,說明可以滿足機理覆蓋,卻不能滿足數值覆蓋,預測精度顯然不高。當溫度出現0℃時,級比甚至連機理覆蓋都無法滿足。因為當0做分子時,級比為0,遠遠小于0.135 3;當0做分母時,級比不可知。所以為了解決這個問題,可以使用“相對溫升”來建立有序數列。相對溫升是指軸溫相對于環境溫度的升幅。

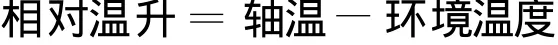
由于列車運行中軸溫總是高于環境溫度,當軸溫為負值時,環境溫度也為負值,由此可知,相對溫升必然是正值。使用相對溫升建立的有序數列在相鄰溫度差異不大于7℃時是完全滿足機理覆蓋的,也就是說建模是可行的。

為了提高預測精度和降低運算量,在相對溫升較小時可以不進行建模。從軸溫運行規律來看,相對溫升較小時進行預測也沒有多大意義。那么在相對溫升為多少時進行建模比較合適呢?通過計算,得到如表1所示的結果。

結合現場實際,選取序號11的數據,既能進行高精度建模,又不會延誤后期預報。因為當相對溫升低于30℃時,軸溫基本屬于正常波動,完全可以不做運算處理;當相對溫升高于30℃時,就需要引起警戒,利用GM(1,1)建模來測知軸溫的下一步變化趨勢,再根據趨勢及時發出警報。為了確保相鄰數據差異小于5℃,可以通過限幅濾波法對高于5℃的脈沖干擾進行“削頂”處理,以保證數列的平滑性。

表1 不同溫升和相鄰溫差的級比

3 設計過程

使用GM(1,1)模型進行建模的詳細步驟可以參考文獻[8]中相關內容,主要是對非負序列作一次累加計算,生成AGO(Accumulated Generating Operation)序列,并構造AGO序列的均值矩陣,再應用最小二乘法,計算出GM(1,1)模型的辨識參數a和u,最終求得GM(1,1)模型的解。考慮嵌入式實時應用,采用了求取中間參數的方法,計算量小、速度快。

詳細過程如下,其中步驟(4)～(8)參考了文獻[8]的有關內容:

(1)計算環境溫度T0

某個軸溫報警器采集的環境溫度過低,將極有可能產生誤報,因此有必要對全車的環境溫度計算平均值,建立環境溫度的統一標準值T0。

(2)求相對溫升dT

利用軸溫T減去環境溫度T0得到相對溫升dT,如果dT＞30,則開始記錄數據。

(3)生成初始序列X(0)

收集夠11個數據,分別計算相對溫升dT(k),建立初始序列X(0)。

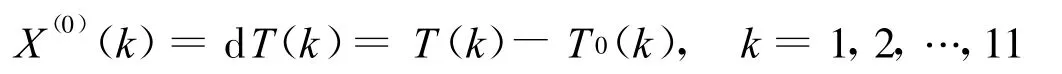
(4)求X(0)的AGO序列X(1)

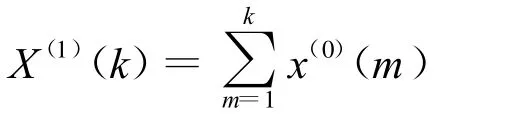
(5)求X(1)的均值序列Z(1)

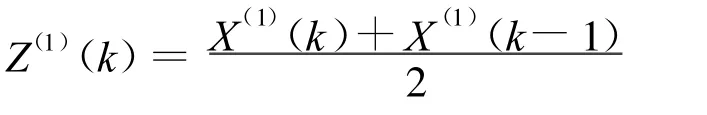
(6)求中間參數C,D,E,F

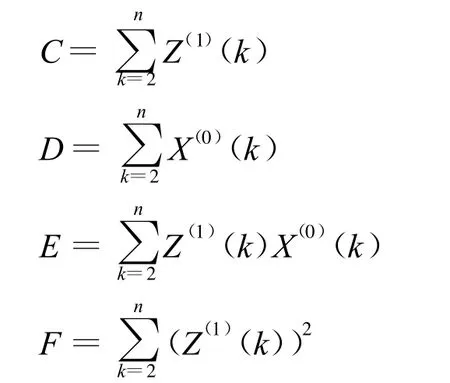
(7)計算參數a和u

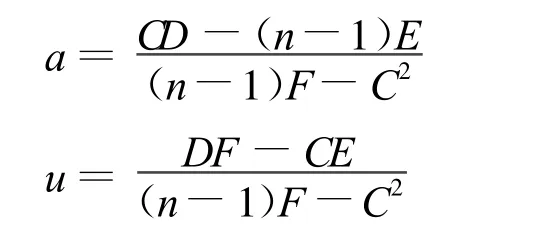
(8)計算預測值＾X(0)

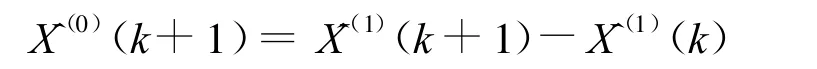
(9)判斷預測值是否超標

＾X(0)(k+1)＜45為正常,否則為超標。

(10)新陳代謝循環建模

不斷將新數據加入,去除最早的數據,保持數列的維度始終為11個。這樣做的好處是提高了預測的精度,同時又不增加計算量,比較適合實時應用。

4 試驗驗證

選取2008年6月22日22:30—23日7:00的Z11次列車YW25T675498軸溫報警器IC卡記錄數據進行建模分析,并將預測數據和實測數據進行擬合對比,如圖1所示。通過對比可以發現,軸溫報警器采集的軸溫最高不超過45℃,數據曲線局部波動較大,干擾較多;而使用新陳代謝預測模型進行預測的結果則有所不同,數據曲線變化較為平緩,趨勢明確,并有4次溫度超過45℃,及時地進行了預警。

文獻[3]記載2008年6月23日0:15該次列車在大劉莊停車檢查,使用點溫計測量軸溫為79℃,與軸溫報警器顯示溫度相差9℃;外溫28℃,與軸溫報警器顯示溫度基本一致。實際溫升51℃,軸溫報警器計算溫升為42℃,采用GM(1,1)模型的報警算法在2008年6月23日0:30計算溫升為48℃,及時地預報了熱軸,與實際情況基本相符。

通過多次對不同列車的軸溫數據進行分析、比對,可以發現GM(1,1)模型基本反映了真實軸溫變化的規律,相對于實測軸溫曲線,預測軸溫曲線更顯平滑,更具規律性,在較短的時限內能夠真實反映軸箱溫度的變化趨勢。

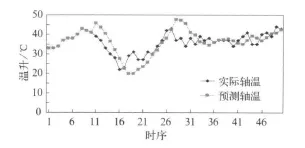
圖1 實際軸溫與預測軸溫擬合圖

5 結束語

給出了一種相對簡單,但精度較高的軸溫預測算法。利用GM(1,1)模型對軸溫數據進行循環建模,根據下一時刻軸溫上升速率是否超標判斷軸承故障。實現了在現有設備條件下的軸溫趨勢預測。經歷史數據驗證,該算法提高了現有軸溫報警器的預報精度,能夠發現軸承早期故障。在TCDS車載主機QNX環境下容易實現,同樣也可以應用到紅外線軸溫探測系統中,實現基于歷史軸溫序列的熱軸判別模型。

[1] 楊志強.客車電氣裝置[M].北京:中國鐵道出版社,2006.

[2] 劉瑞揚.北美鐵路車輛安全軌邊檢測系統的現狀及思考[J].中國鐵路,2004,(7):57-60.

[3] 劉永林.淺談一起25T型客車熱軸的原因分析[J].鐵道機車車輛,2009,29(3):66-67.

[4] 張運剛,溫曉敏,姚熊亮.運行列車軸溫規律的模糊分析[J].鐵道學報,1996,18(3):20-28.

[5] 鄧聚龍.灰色系統理論教程[M].武漢:華中理工大學出版社,1990.

[6] Deng Julong.On judging the admissibility of grey modeling via class ratio[J].The Journal of Grey System,1993,(4):249.

[7] 許立群,況守忠,詹奎吉,婁維祥.檢車乘務員在途中如何處理客車熱軸燃軸[J].鐵道車輛,1998,36(9):53-55.

[8] 鄧聚龍.灰預測與灰決策[M].武漢:華中科技大學出版社,2002.