常見電路的動態分析問題的解法實例

宋振全

(江蘇省睢寧高級中學南校,江蘇睢寧 221200)

電路的動態分析問題是歷年高考選擇題中必考的習題,這類問題著重考查的學生的應用基本知識分析問題的能力,具有很強的靈活性,學生做這些問題時易出錯,下面筆者結合具體習題談一談這類問題的解法.

1 閉合電路的電壓電流的動態變化分析

例1.如圖 1所示的電路中,R1、R2、R3、R4皆為定值電阻,R5為可變電阻,電源的電動勢為 E,內阻為r.設電流表A的示數為I,電壓表V的示數為U,當滑動觸頭向上移動時

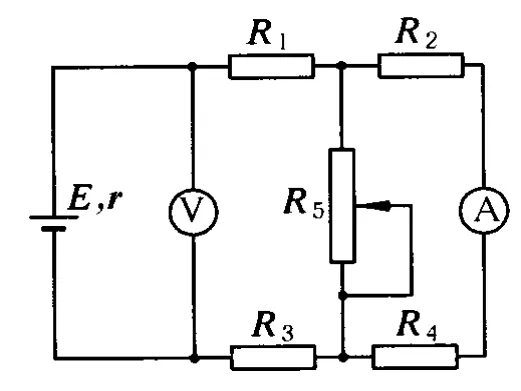
圖1

(A)I變大,U變小.

(B)I變大,U變大.

(C)I變小,U變大.

(D)I變小,U變小.

解析:整個電路的連接形式為 R2、R4串聯后與電阻R5并聯,然后再與電阻 R1、R3串聯接在電源上,電壓表測量的是路端電壓,電流表測量的是流過 R2、R4的電流,當滑動觸頭向上滑動時R5接入電路的阻值變小,R2、R4串聯后再與 R5并聯的這部分電阻減小,這部分電路再與R1、R3的串聯的總電阻值也減小,即外電路的總阻值變小,所以,根據閉合電路歐姆定律,干路中的總電流增大,路端電壓變小,所以電壓表的示數應該變小,R2、R4兩端的電壓減小,電流表的示數應變小,所以正確的答案為(D).

方法歸納:(1)解題先明確電流表和電壓表是測量哪一部分的電流和電壓和各個電路元件的連接情況.(2)電路中無論各元件是串聯、并聯還是混連,只要其中任何一個電阻變大,總電阻就隨之變大,反之總電阻變小.電路中如有開關控制的電路與此相似,若開關通斷使串聯的用電器增多則總電阻增大,若開關的通斷使并聯的用電器增多則總電阻減小.(3)這類問題的解題基本解題思路為“部分→整體→部分”,即從電阻的變化的部分入手,再由閉合電路歐姆定律判斷 I總和U路端的變化情況,最后再判斷部分電路的I和U變化情況.(4)根據滑動變阻器的阻值變化情況,可以用“串反并同”來判斷變阻器并聯的電路和變阻器串聯的電路中的電流和電壓的變化,“串反”即與變阻器串聯的電流表或用電器中的電流變化與變阻器的阻值變化相反,也就是變阻器的阻值變大用電器的電流就變小,變阻器的阻值變小用電器的電流就變大.“并同”是指與變阻器并聯的那部分電路中電壓的變化和電流的變化和變阻器阻值的變化相同,即變阻器的阻值增大與變阻器并聯的那部分電路的電流和電壓都增大,反之亦然.

2 閉合電路中的電流和電壓變化量的分析

例 2.(2006上海)在如圖2所示的電路中,閉合開關S,當滑動變阻器的滑動觸頭 P向下滑動時,4個理想電表的示數都發生變化,電表的示數分別用 I、U1、U2和 U3表示,電表示數變化量的大小分別用ΔI、ΔU1、ΔU2、ΔU3表示.下列比值正確的是

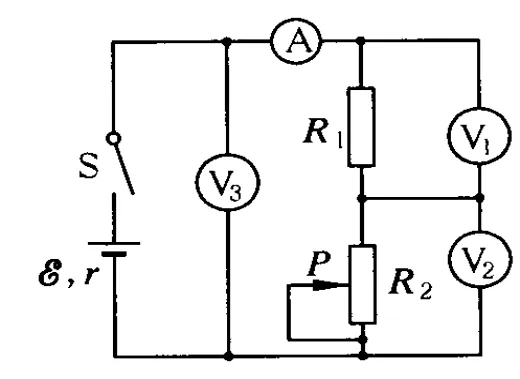
圖2

方法歸納:(1)討論此類問題時涉及到變化量可以根據閉合電路歐姆定律將電路分為內電路和外電路.由于電動勢是定值,所以內外電路的的電壓變化量相同,即ΔU內=ΔU外.(2)可以將定值電阻等效地看成電源的內阻,處理習題會很方便,上題中我們如果將 R1和電源看成一個整體,這時電源的電動勢為E,內阻就是R1+r.由此我們還知道U1減小,U2增大,但 U1減少量和 U2的增加量不相等,而是ΔU1＜ΔU2,具體一些說應該是ΔU2=ΔU1+ΔUr.

3 滑動變阻器連接所形成的對稱電路問題

例3.如圖 3所示,電源的電動勢E=8 V.內阻不為零,電燈A標有10 V,10 W的字樣,電燈B標有 8 V,20 W 的字樣,滑動變阻器的總電阻為6 Ω.閉合開關 S,當滑動觸頭從上向下滑動的過程中(不考慮電燈電阻的變化)則

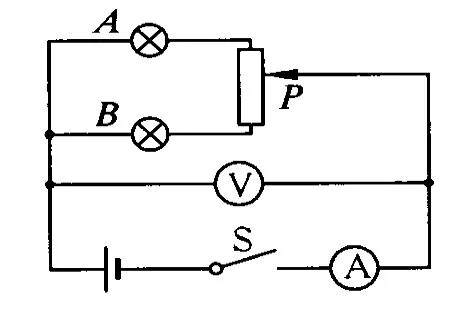
圖3

(A)電流表的示數一直增大,電壓表的示數一直減小.

(B)電流表的示數一直減小,電壓表的示數一直增大.

(C)電流表的示數先增大后減小,電壓表的示數先減小后增大.

(D)電流表的示數先減小后增大,電壓表的示數先增大后減小.

解析:由圖知 A燈、B燈、滑動變阻器組成的電路中,滑動變阻器分成兩部分聯入電路,設與 A燈連接的那部分電阻為RX,滑動變阻器的電阻為 R,這部分電路的有效電阻大小為

方法歸納:滑動變阻器分成兩部分分別聯入兩個支路中時,當滑動觸頭滑動時,使兩個支路的電阻分別相等時,這樣的電路稱為對稱電路,這時電路中的總電阻最大.如上圖,如果不能形成對稱電路,則當兩個支路的阻值越接近其總阻值越大,反之則越小.先由電阻的變化再判斷其他物理量的變化.

4 電路的故障問題

例4.如圖4所示的電路,閉合開關 S后,燈 L1、L2都能發光,后來由于某種故障使燈L2突然變亮(未燒壞),燈 L1變暗,電壓表的讀數增大,由此可推斷,這故障可能是

(A)電阻 R1斷路.

(B)電阻 R2短路.

(C)燈L1兩接線柱間短路.

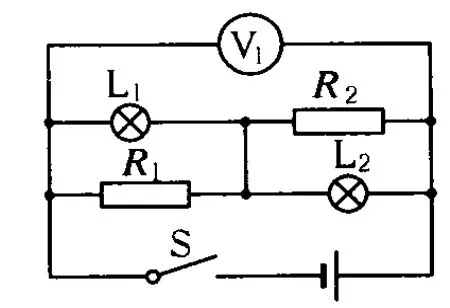
圖4

(D)電阻 R2斷路.

解析:由圖知,電壓表測路端電壓,當其讀數突然增大,據閉合電路歐姆定律知,外電路總電阻增大.同時燈L2變亮,說明L2兩端的電壓增大.所以故障一定是R2斷路,正確答案為(D).

方法歸納:電路中某部分出現斷路,因斷路部分的電阻無窮大,可以理解為這部分電路的電阻增大,而且增至無窮大.電路中某部分出現短路,因短路部分的電阻接近零,所以可以認為這部分電阻減小,而且減小至零,這樣就可以確定總電阻的變化.再結合閉合電路歐姆定律處理其他問題.

5 直流電路中接有電感線圈時,電路的通斷所引起的動態變化分析

例5.(2008年江蘇)如圖5所示的電路中,3個相同的燈泡 a、b、c和電感L1、L2與直流電源連接,電感的電阻忽略不計.電鍵S從閉合狀態突然斷開時,下列判斷正確的有

(A)a先變亮,然后逐漸變暗.

(B)b先變亮,然后逐漸變暗.

(C)c先變亮,然后逐漸變暗.

(D)b、c都逐漸變暗.

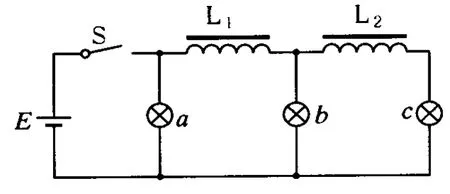
圖5

解析:電路穩定工作時,由于電感的電阻不計,3燈泡中的電流相同,亮度一樣.開關斷開后,電路中的電流發生變化,但由于電感線圈發生自感作用,電路中的電流不會發生突變,而是漸變,即電流從原來的值緩慢地減小到零.若斷開前每個燈泡中的電流為 I0,則圖中電感L1中的電流I1=2I0,L2的電流I2=I0,所以斷開后的瞬間燈b和燈c中的電流仍與斷開前一樣大小為I0,而燈 a的電流為2I0,然后他們逐漸地減小,所以本題選(A)、(D).

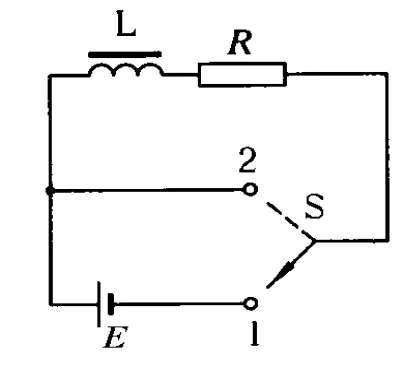
圖6

方法歸納:(1)、自感現象通常情況下分為通電自感和斷電自感,根據 LR電路的暫態過程的理論分析(見趙凱華、陳熙謀編著的《電磁學》),電路中的電流按指數規律變化,在圖6中S打向1后,L中的電流變化規律為i=,當開關撥到2時,L中的電流變化規律為i,其電流隨時間變化的圖像如下圖7和8所示.

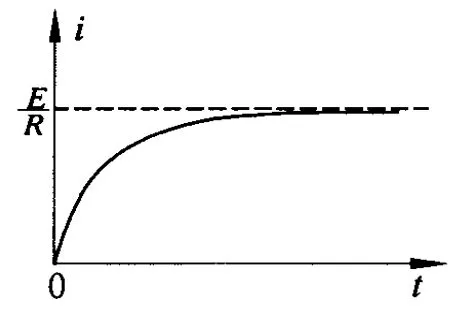
圖7

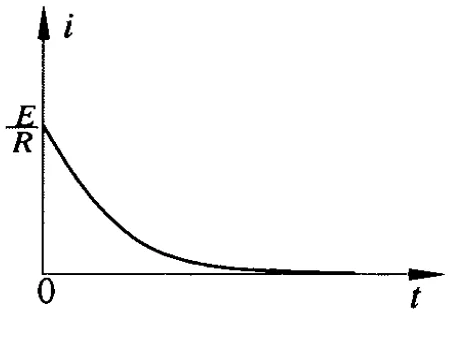
圖8

(2)燈泡的變亮還是變暗取決于開關斷開前后通過燈泡電流的變化情況,上題中開關斷開前后瞬間b燈和c燈的電流一樣,而a燈的電流加倍,所以a燈的亮暗變化情況和b、c兩燈不一樣.

6 接有電感和電容的的直流電路動態變化問題

例6.如圖9所示電路中,L為電感線圈,C為電容器,當開關S由斷開變為閉合時,則

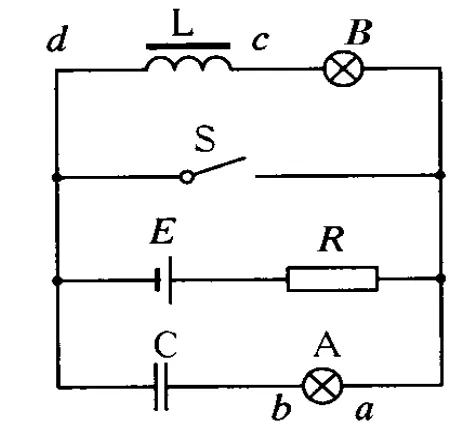
圖9

(A)A燈有電流通過,方向由a到b.

(B)A燈中無電流通過,不可能變亮.

(C)B燈立即熄滅,c點電勢低于d點電勢.

(D)B燈逐漸熄滅,c點電勢低于d點電勢.

解析:開關閉合前,電容器的支路中沒有電流,但電容器被充電,兩極板帶上等量的異種電荷,且燈A不亮,電感線圈的電路有電流通過,燈泡發光.開關閉合時上述的兩個支路被短路,所以就形成線圈 L→燈B→線圈L以及電容C→燈 A→電容 C的兩個閉合回路.電感線圈發生自感,電容器放電,所以選(D).

方法歸納:(1)直流電路中,連接電容器的電路在電路穩定時相當于斷路,但電容器兩極板卻帶電.兩極板間的電壓等于和電容器的電路并聯的那部分電路兩端的電壓,在充電和放電的瞬間,電路中存在瞬時電流.(2)電感線圈發生斷電自感時,線圈相當于電源,電流流出的一端相當于電源的正極.

7 接有變壓器的交流電路動態變化分析

例7.如圖10所示,是變壓器通過降壓給用戶供電的示意圖.變壓器輸入電壓是市電網的電壓,不會波動,輸出電壓通過輸電線輸送給用戶,輸電線的電阻用R0表示,變阻器的R表示用戶用電器的總電阻,當滑動變阻器的觸頭向下移動時,下列說法中正確的是

(A)相當于在增加用電器的數目.

(B)V1表的示數隨V2表的示數的增大而增大.

(C)A1表的示數隨A2表的示數的增大而減少.

(D)變壓器的輸入功率在增大.

解析:選(A)、(D).因為用戶的用電器都是并聯的,并聯的用電器越多,電路中的電阻越小.接入的用電器越多用戶消耗的功率越大,理想變壓器工作時輸出功率和輸入功率相同,所以選(A)、(D).

圖10

8 交變電流電路中接有電感和電容的動態變化問題

例 8.如圖 11 所示,交流電表 A1、A2、A3分別與電容器、線圈L和電阻R串聯后接在同一個交流電源上,供電的瞬時電壓值為 u1=Umsinω1t,3個電表各有不同的讀數.現在換一個電源供電,供電電壓的瞬時值為 u2=Umsinω2t,ω2=2ω1.改換電源后,3個電表的讀數怎樣變化?

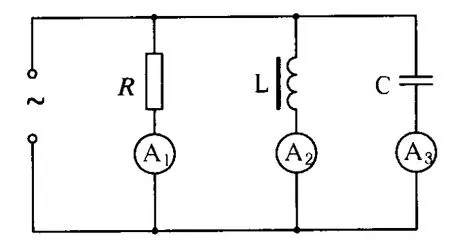
圖11

解析:A1表的示數不變,由電感線圈對交變電流的阻礙作用我們稱之為感抗,其大小為 XL=2πfL=ω L,ω2=2ω1,阻礙作用變大,A2的示數變小,電容對交變電流阻礙作用,我們稱之為容抗,其大小為,所以A3的示數變大.

方法歸納:電阻對交流電的阻礙作用與交流電的頻率無關,電感線圈連接在電路中時,線圈對交變電流有“通低頻,阻高頻”的作用,交流電的頻率越大,其對電流的阻礙作用越大.電容器對交變電流的作用是:“隔直流、通交流,阻低頻、通高頻”,交變電流的頻率越大,電容器的阻礙作用就越小.

總之,對于電路的動態分析問題,我們只要把握這類問題的規律,從根本上找到這類問題的解決辦法,一定會在高考中少犯錯誤.