高中物理習題教學的優化策略

張丹彤

(揚州市教育局教研室,江蘇揚州 225007)

高中物理教學過程中,習題教學貫穿始終,是中學物理教學的重要環節之一,是教學效果反饋的重要渠道.除了專門的習題課、試卷講評課外,新授課、實驗課中也會涉及例題講解和課后練習的講評.在教學實踐中我們感到,即使師生常年在習題中滾打,但提高學生的解題能力依然是個難題,學生在考試中還是會出現諸如容易的題做錯,經常講的題做不對,稍難一點的題不會做等現象.這種現象與平時習題教學的簡單化、粗獷式、不遵循思維規律、只求數量不重質量等有著直接的關系.

要提高學生的成績和教學效率,習題教學應該進一步優化.教師在習題教學的過程中應該加強研究,充分把握學生的成長規律,深刻領會學生的思維規律,深入研究教材,勇于創新,概括起來要做到就是“四求”.

1 求是——選擇合適起點,反對一步到位

求是就是要求我們遵循規律,要遵循人的成長規律和思維規律.高中3年盡管在同一個學段,但高一學生在身體、心智等方面跟高三比還是有著明顯差距的.對一個剛接觸高中物理的高一學生而言,我們應該立足于培養學習興趣和良好的習慣.新課中的例題和新課后的練習,其目的應側重于對本課所學知識的正確理解,以突出本課內容為主,應避免選擇綜合性較高的題目,不應強行“一步到位”.

例如,有教師在“熱力學第一定律”新課中選用某年高考題作為例題,題及分析過程如下:

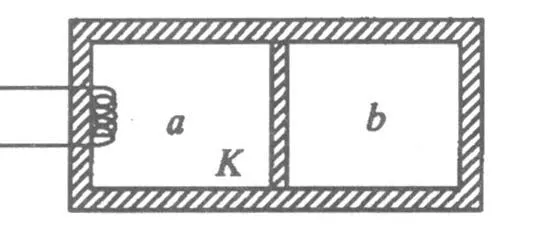
圖1

例1.如圖1所示,絕熱隔板K把絕熱的氣缸分隔成體積相等的兩部分,K與氣缸壁的接觸是光滑的.兩部分中分別盛有相同質量、相同溫度的同種氣體a和b.氣體分子之間相互作用勢能可忽略.現通過電熱絲對氣體 a加熱一段時間后,a、b各自達到新的平衡

(A)a的體積增大了,壓強變小了.

(B)b的溫度升高了.

(C)加熱后a的分子熱運動比b的分子熱運動更激烈.

(D)a增加的內能大于b增加的內能.

分析:(1)a加熱后若體積不變則壓強比b大,因而活塞向右移動.(氣體定律)

(2)重新平衡后 a、b壓強相等.(平衡條件)

(3)活塞對b做功導致b內能增大,b溫度升高,選項(B)正確.(熱力學第一定律)

(4)b溫度升高、體積縮小導致 b的壓強增大,選項(A)不正確.(氣體定律)

(6)a的溫度升高比b多,a增加的內能比b多,選項(D)正確.(內能的概念)

由上述的解析過程,可以看出:本題只有選項B涉及熱力學第一定律問題,而比較難確定的問題蘊含在選項(C)、(D)中,因此學生在解決本題時的思維活動主要圍繞著綜合運用氣體定律的知識來進行,盡管這是一道好題,但如果把它作為熱力學第一定律新課后的練習題,則對學生全面理解、鞏固熱力學第一定律會產生較大的干擾作用.

2 求真——遵循思維規律,反對生搬硬套

求真就是要求我們在遵循規律的基礎上,引導和培養學生正確的態度和科學的思維方法.大家都有這樣的體會,學生在遇到陌生復雜問題時常常會搜索記憶中教師講過或自己做過的題型,看本題和哪種類型的例題吻合,套用解答這種例題的公式,甚至直接硬套例題的結論,其思維方式是“機械模仿,簡單遷移”.毫無疑問,高考題中不可能出現完全重復的題目,“機械模仿式”的思維方式不可能應對高考中不斷創新的物理問題.在教學過程中,我們應該堅持“具體問題具體分析”這個真理,逐步養成學生求真務實的良好品質,在平時教學中要注意引導學生在草稿紙上畫思維導圖,逐步養成手、眼、腦并用的分析習慣.

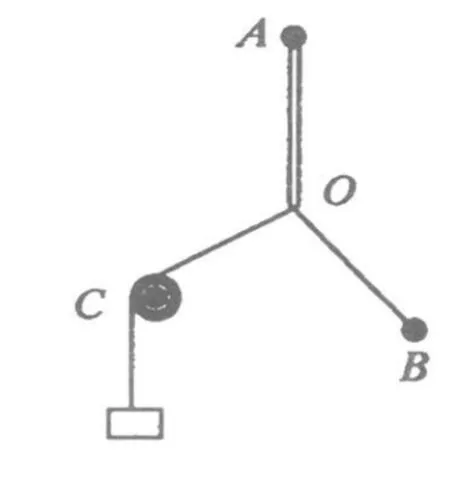
圖2

圖3

例2.如圖2,AO是橡皮繩,BO為不能伸長的細繩,A、B點固定在木板上,木板豎直放置.繩OC穿過定滑輪(摩擦不計),其下端懸吊一個砝碼.此時 O點到達一定的位置.問:如果任意改變定滑輪的位置,是否還可以找到不在OC直線上的另一處,也能使結點O到達原來的地方?

解題的思維過程分解如下表所示:

通過上述思維過程的慢動作回放,我們應該體會到,解決物理問題的思維過程關鍵在于分析,學生掌握了正確分析的方法,距離解題成功就不遠了.本題中只要BO與OC的夾角不等于90°,就一定可以找到另一處符合題意的平衡位置.

3 求變——倡導舉一反三,反對就題論題

求變一方面要求教師善于從教材上的例題、習題和我們熟悉的常見問題(陳題)出發,進行有效的改造和變化,通過變化,可以從平易中變出精彩,從而提高學生的學習興趣,激發學生的求異思維.應該說幾乎所有的物理習題都可以進行改造和變化,教師充滿智慧的求變并有意識地引導學生從“變”的現象中發現“不變”的本質,能夠不斷促進學生的有效思維,提高學生的思維品質.

改造和變化習題一般可以按照逆向反推(物理條件和所求結論之間互換)、縱向延伸(在一個相對簡單問題的基礎上前延后伸)、橫向拓展(物理量或物理規律之間發生較為復雜的橫向聯系,形成綜合)等方法進行.高考試題中這類問題經常出現,如測定金屬導體的電阻率這樣一個常規物理實驗在江蘇省2009年高考試卷上拓展為測定一個圓臺形導體的電阻率;江蘇省2010年高考試卷選擇題第3題求照相機三腳架每根支架中承受的壓力大小,實際上是把平時常見的平面內的力的合成與分解拓展為空間的力的合成與分解;上海市2010年高考試卷中出現的一正兩負3個電荷的靜電場問題是從最常見的等量同種和異種電荷的電場變化而來的,輕靈一變,題目變得更精彩,考查學生能力更有效.

4 求新——勇于創新探索,反對因循守舊

求新就是不斷追求題目創新,常見的方法一般是把物理學新的發展成果作為命題背景,或者是以生產生活中的實際應用作為命題的背景并賦予新的應用,或者是在常見物理現象中選擇新的視角作為命題的原則,或者創設新的物理情景并在新情景下考查學生的各種能力.求新要求我們要不斷學習,關注物理學的最新發展動態;要求我們深入研究,不斷在司空見慣的物理問題中尋找新視角,創設新情景,探究新發現.

2004年高考江蘇卷第7題就是一條體現“新”的試題,該題以雷蒙德·戴維斯因研究來自太陽的電子中微子(νC)而獲得了2002年度諾貝爾物理學獎的最新成果作為命題背景,用這一即使在近代物理中也是很新的內容來考查高中學生靈活運用所學知識分析解決問題的能力.

再看一例:

例3.(2010年高考江蘇物理卷第5題)空間有一沿 x軸對稱分布的電場,其電場強度 E隨x變化的圖像如圖4所示.下列說法正確的是

(A)O點的電勢最低.

(B)x2點的電勢最高.

(C)x1和-x1兩點的電勢相等.

(D)x1和 x3兩點的電勢相等.

圖4

討論:本題僅給出一個比較罕見的E-x圖像,沒有其他信息可用,由于這種場強空間變化問題高中階段非常少見,面對本題,不少學生讀不懂圖像,感到無從下手.

暫且不去討論本題,而來看另一個問題:等量同種電荷電場線分布是高中生非常熟悉的模型,學生可以比較容易地畫出電場線的分布圖,但很少關注場強大小變化的情況.借助這一模型我們來創設這樣一個新問題:

如圖5,等量同種電荷處在一豎直線上,過兩電荷的中垂線作一 x軸,x軸與兩電荷連線的交點為原點,試定性在圖6中畫出 x軸上的電場強度E隨x變化的E-x圖線.

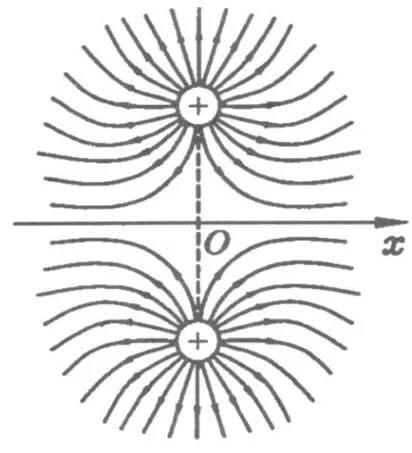
圖5

圖6

討論:顯然,在 O點場強為0.沿 x軸正向很遠處,場強趨近于0.從O點沿x軸正向,場強先逐漸增大,再逐漸減小,途中某處場強一定有一個最大值,因此可定性畫出沿x軸正向的E-x圖線,再根據對稱性可以畫出完整的圖像如圖7所示.

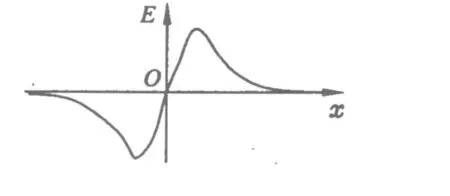
圖7

到這里我們應該能發現,前面題中出現的E-x圖線原來是我們非常熟悉的等量同種電荷的沿中垂線的場強變化圖線,至此,解決這一問題就變得十分容易:由熟悉的等量同種電荷的等勢線分布圖不難知道,在 x軸上O點電勢最高,x1和-x1兩點處在同一等勢線上.

本例是一個非常精彩的創新案例,它從非常熟悉的問題情景中以一個獨特的視角作為命題背景,能夠很好地考查學生的聯想能力.本案例同時也給我們一個啟示,創新并不神秘,完全可以從教材中、從平時熟悉的模型中去尋求創新問題.

在當前新課程背景下,提高課堂效率已經成為廣大教師的共識,但提高學生訓練效率更應得到重視.如果教師能進一步遵循學生思維規律,不斷研究物理習題,研究習題的解法,讓學生感受更新、更活、更精彩的物理問題和更有效的解法,減少隨意、雜亂和無意義的重復,一定可以達到激發學生學習興趣,提高教學質量的目的.