Auto-regressive模型在全國嬰兒死亡率擬合中的應用

濰坊醫學院預防醫學系(261053) 劉 松 李曉妹 劉 健 劉曉冬 李向云

嬰兒死亡率〔1〕(infant mortality rate，IMR)是反映居民健康水平、社會經濟及衛生服務水平和婦幼衛生服務質量的敏感性指標。據衛生部統計，我國的嬰幼兒死亡率由 1991年的 50.2‰下降到2007年的15.3‰〔2〕，總體上呈下降趨勢。但與世界上其他國家相比，我國的嬰兒死亡率仍然較高〔3〕。本文利用Autoregressive模型擬合我國嬰兒死亡率的變化趨勢，在評價其效果的基礎上探討殘差自回歸模型在其他非平穩時間序列數據擬合中的適用性。

資料和方法

1.資料來源 本文所利用的數據為我國1991～2007年的嬰兒死亡率，來源于國家衛生部《2008中國衛生統計年鑒》，數據真實可靠。

2.統計方法 運用Auto-regressive模型對我國1991～2007年嬰兒死亡率數據序列進行擬合;應用SAS 8.2統計軟件對資料進行統計學分析〔4〕。

3.Auto-regressive模型建模步驟

(1)確定性因素分解〔5〕

在自然界中，由確定性因素導致的非平穩，通常顯示出非常明顯的規律性，比如有明顯的趨勢或者有固定的變化周期，這種規律性信息通常比較容易提取，而由隨機因素導致的波動則非常難以確定和分析。根據這種性質，人們經過長期的觀察和實踐，通常把序列分解為三大因素的影響:

①長期趨勢波動，包括長期趨勢和無固定周期的循環波動。

②季節性變化，包括所有具有穩定周期的循環波動。

③隨機波動，除了長期趨勢波動和季節性變化之外，其他因素的綜合影響歸為隨機波動。

(2)殘差自相關檢驗

①檢驗原理

確定性模型擬合好之后，我們要對該模型的擬合效果進行檢驗。

如果殘差序列顯示出純隨機的性質，即

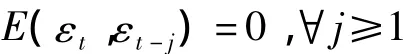
就說明確定性模型擬合非常好，已經能夠充分提取序列中的相關信息，我們不需要再對序列進行二次信息提取，分析結束。

反之，如果殘差序列顯示出自相關性，即

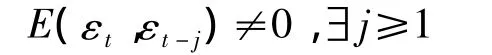
那就說明確定性模型擬合得不夠精確，序列中的相關信息沒有得到充分提取，我們應該對殘差序列再次擬合，提取其中殘存的相關信息，以提高模型擬合的精度。

②殘差自相關檢驗:Durbin-Waston檢驗(簡稱DW檢驗)

下面以殘差1階自相關性檢驗為例介紹DW檢驗的原理。

原假設:殘差序列不存在1階自相關性，即

備擇假設:殘差序列存在1階自相關性，即

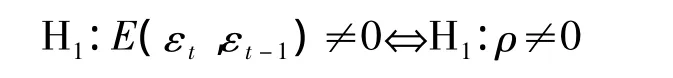
構造DW檢驗統計量:

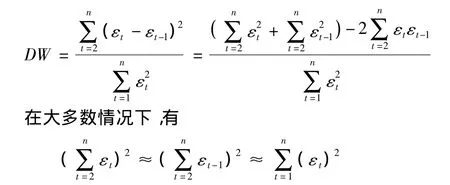
所以DW檢驗統計量近似等于:

即DW?2(1－ρ)，因為 －1≤ρ≤1，所以0≤DW≤4。當0＜ρ≤1時，序列正相關;當 －1＜ρ≤0時，序列負相關。

(3)Auto-regressive模型的建立

①確定自回歸模型的階數

根據模型的自相關圖和偏自相關圖，確定模型殘差序列的自相關階數。

②參數估計

根據原序列回歸模型的口徑，可以確定殘差序列的值。單純根據殘差序列的值可以非常容易地確定殘差自回歸模型的口徑。但是由于殘差序列與序列回歸值之間具有相關性，所以在將他們分開時不要忽略相關性的影響，否則會降低模型擬合的精度。所以，參數最優估計是在上述分析的基礎上，確定回歸模型的結構和殘差自回歸模型的階數，將所有參數聯合求解。

4.評價模型

根據確定系數R2對模型的擬合效果進行評價，以此判斷該模型在對我國嬰兒死亡率進行擬合的適用性和有效性。

結 果

1.平穩性檢驗

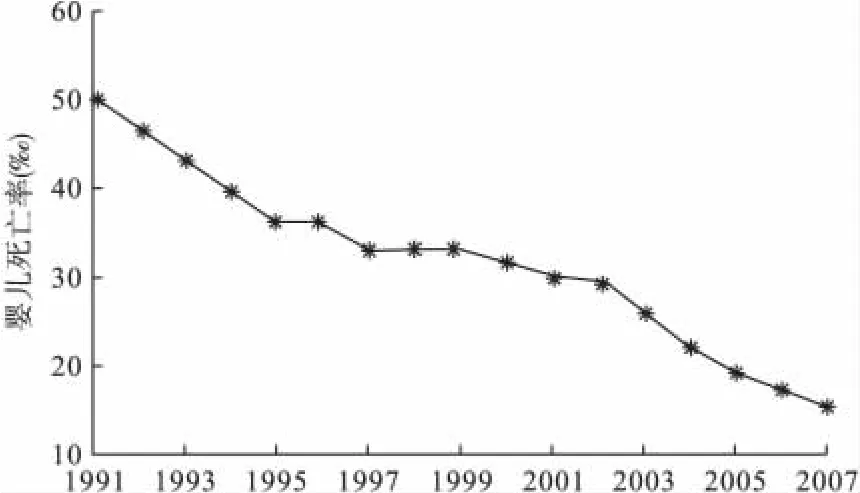
圖1 我國1991～2007年嬰兒死亡率序列時序圖

時序圖顯示該時間序列有一個明顯的隨時間線性遞減的長期趨勢，同時又包含一定的隨機信息，因此考慮使用殘差自回歸模型擬合該序列的發展。

2.純隨機性檢驗

純隨機性檢驗也稱為白噪聲檢驗，是專門用來檢驗序列是否為純隨機序列的一種方法。本文采用LB(Ljung-Box)統計量進行檢驗。檢驗結果顯示，在6階延遲下LB檢驗統計量為3.74(P＜0.05)，所以我們可以認為1991～2007年我國嬰兒死亡率數據序列屬于非白噪聲序列。

3.Auto-regressive模型的建立

(1)確定性模型的建立

表1 普通最小二乘估計結果

從表1得出，輸出的確定性模型為:Xt=108.0373－0.005345t+ μt

輸出結果顯示DW統計量的值等于0.5077，輸出概率顯示殘差序列正相關(P＜0.0001)，所以應該考慮對殘差序列擬合自相關模型。

(2)回歸誤差分析

進行回歸誤差分析時，采用逐步回歸向后消除法。逐步回歸向后消除報告顯示除了延遲1階和4階的序列顯著自相關外，延遲其他階數的序列值均不具有顯著的自相關性，因此延遲2階、3階和5階的自相關項被消除。初步均方誤差為1.2485，1階殘差自回歸模型的參數φ1=－0.608073，φ2=0.438357。輸出的自回歸模型結果為:ut=0.608073ut－1－0.438357 ut－4+εt，具體結果詳見表2。

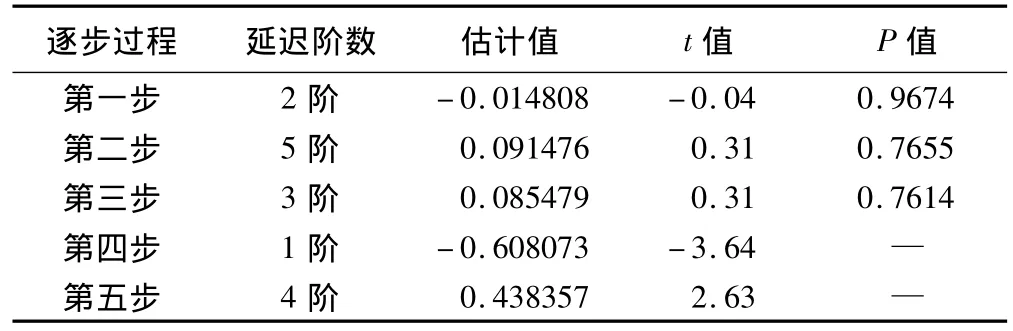
表2 逐步回歸向后消除法誤差分析輸出結果

(3)Auto-regressive擬合模型

該部分輸出三方面的匯總信息:收斂情況、極大似然估計結果和回歸系數估計，輸出結果見表3:

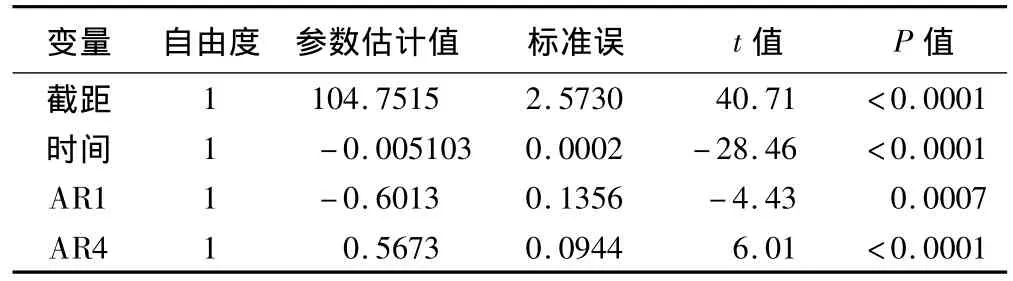
表3 最終擬合模型輸出結果

由表3可得出，最終擬合我國嬰兒死亡率得到的模型為:

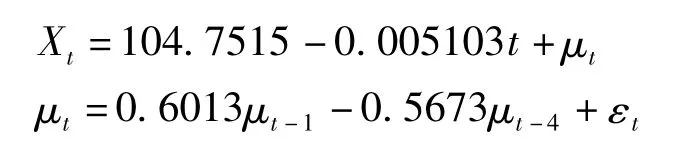
確定系數R2為0.9857，表明該模型所能解釋的變異占全部變異的98.57%，比確定模型的決定系數R2=0.9627要大，證明模型擬合較好。

為了得到直觀的擬合效果，利用SAS程序輸出擬合效果圖(圖2)。

圖2 Auto-regressive模型擬合效果圖

擬合效果圖中，星號表示實測值，實線表示Xt=104.75－0.005103t+μt的直線擬合，虛線表示整體模型 μt=0.6013μt－1－0.5673μt－4+ εt的曲線擬合。

討 論

以往的研究多利用線性模型、指數模型等來探討影響嬰兒死亡率的相關因素〔6，7〕，如殷菲等采用徑向基函數神經網絡建立預測模型對嬰兒死亡率進行預測;喬曉東等利用重復測量的多水平模型分析衛生Ⅷ項目縣8年監測資料等。因為線性模型、指數模型、logistic回歸模型等對資料的要求都比較嚴格，這些方法只能提取確定性信息，對隨機性信息浪費嚴重。而Auto-regressive模型是一種擬合非平穩時間序列的方法，兼具了時間序列確定性分析和隨機性分析的優點，它既能提取序列的確定性信息，又能提取其隨機性信息。本文利用我國1991～2007年間嬰兒死亡率的數據，時序圖顯示其具有長期變化和隨機波動的非平穩特征，若僅用一般線性回歸進行擬合，殘差序列會存在自相關性，提示對序列信息的提取不充分。因此考慮選用Auto-regressive模型來擬合，效果較為理想。

由于醫學、農業、工業、氣象、經濟等領域中的諸多現象都具有時間序列的特征，殘差自回歸模型的應用也日趨廣泛。尤其在生物醫學領域，如我國婦幼衛生監測網監測的出生缺陷率、孕產婦死亡率以及多種傳染病的發病率等都具有非平穩時間序列的特征，可利用殘差自回歸模型對其進行擬合和預測。因此，Autoregressive模型具有良好的應用和發展前景。

同時，本研究也存在一定的局限性。嬰兒死亡率受到多方面的影響，如衛生資源的配置、衛生服務的利用、經濟發展狀況和居民收入等，并且各種因素對嬰兒死亡率影響的程度、方式、途徑等都有各自的特點。所以在Auto-regressive模型的推廣應用中要慎重加以考慮，否則會致使結果可能出現一定的偏差。

1.黃書香.認真貫徹落實《兩綱》指標，提高婦女兒童健康水平.中國婦幼保健，2007，22(19):2609-2610.

2.衛生統計年鑒，中華人民共和國衛生部.2009.

3.劉婭，葉運莉，袁萍.中國嬰兒1991～2004年死亡率趨勢及預測分析.現代預防醫學，2007，34(16):3101-3105.

4.劉曉冬，景睿，孟祥臻，等.殘差自回歸模型及SAS程序實現.中國衛生統計，2008，25(5):550-551.

5.王燕.應用時間序列分析.北京:中國人民大學出版社，2005.

6.殷菲，潘曉平.基于徑向基函數神經網絡的嬰兒死亡率預測模型.現代預防醫學，2006，33(4):486-487.

7.喬曉東，吳擢春，高艷，等.衛生Ⅷ項目地區嬰兒死亡率影響因素的多水平分析.中國衛生統計，2009，26(1):49-51.

附錄:SAS程序