大功率變速恒頻雙饋風力發電變流控制技術*

易一鵬， 成思琪 莊圣賢， 程遠銀

(1.西南交通大學電氣工程學院，四川成都 610031;2.四川大學電氣信息學院，四川成都 610064)

0 引言

近年來，風力發電因其獨特的優勢在可再生能源中備受關注。隨著單機功率的不斷增大，大功率雙饋風力發電及其控制技術成為研究熱點。應用于雙饋風力發電中的雙脈寬調制(Pulse Width Modulation，PWM)變換器具有如下優點［1］:直流側母線電容使得兩側變換器解耦控制相對獨立而不互相干擾;變頻器容量只占整機功率的約30%，成本降低;功率雙向流動，諧波污染小，輸入輸出特性好，電網故障情況下擁有較強的適應能力。基于d-q解耦的矢量控制技術在雙饋風力發電系統上的應用，有多種算法已經被相繼提出，文獻［2-3］通過分開控制轉子電流有功、無功分量實現了功率解耦控制和最大風能捕獲;文獻［4］建立了包括并網控制和最大風能追蹤模塊的交流勵磁變速恒頻風力發電仿真系統。

本文首先介紹了由雙饋發電機(Double Fed Induction Generator，DFIG)和背靠背雙PWM變換器組成的變速恒頻風力發電系統的運行原理，通過建立DFIG穩態數學模型、等效電路、功率關系式，著重研究轉子側功率變換器的控制策略，并完成整個雙饋風力發電穩態控制模型。通過搭建仿真模型，驗證該矢量控制策略的有效性。

1 雙饋風力發電系統工作原理

變速恒頻雙饋風力發電系統結構如圖1所示，該系統由風力機、齒輪箱、雙饋發電機、雙PWM變換器組成。槳葉捕獲風能并通過傳動鏈輸出機械能，由DFIG完成機械能向電能的轉換。

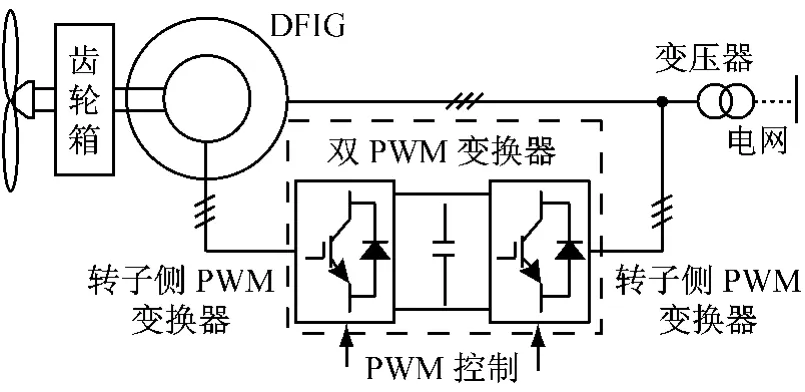
圖1 變速恒頻雙饋風力發電系統結構

為能使發電系統在從次同步到超同步全速范圍內均能得到有效控制，功率變換器必須具備功率雙向流動的能力。當發電機運行于亞同步速時，變頻器向轉子提供勵磁，定子向電網供電;當運行于超同步速時，定轉子同時向電網供電。具體來講，由定轉子旋轉磁勢相對靜止可得:

式中:f1——定子電流頻率;

pn——極對數;

nr——轉子轉速;

fs——轉子電流頻率。

發電機的轉速nr隨著風速而變化時，PWM變換器通過調整轉子輸出勵磁電流的頻率fs，使定子繞組輸出頻率f1保持恒定，從而實現變速恒頻的發電過程。

功率變換器中的轉子側變換器和電網側變換器各司其職，通常，轉子側變換器用于實現有功功率、無功功率的解耦和最大風能追蹤;網側變換器用于維持直流母線電壓恒定和單位功率因數。

2 風力機模型及最大風能捕獲

風力機是能量轉換的核心部件，直接影響著整個發電系統的性能和效率，分析其從空氣中獲取有效風能的過程至關重要。根據空氣動力學知識，風力機輸出的有效功率被定義為函數關系式［5］:

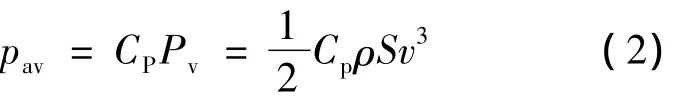
葉尖速比的定義:

風力機輸出轉矩為

式中:Cp——風能利用系數，是關于葉尖速比λ與槳距角β的函數;

Pv——風速為v時對應的風功率;

ρ——空氣密度;

S——槳葉掃風面積;

R——槳葉半徑值;

ω——葉片旋轉角速度;

v——風速;

圖2所示為風力機的特性曲線，其中圖2(a)所示為固定槳距、不同風速情況下，風力機輸出功率與轉速的關系，在某一特定風速下，不同轉速會使風力機輸出不同的功率，且只在某一轉速值處達到最大輸出功率，由這些點即構成了最佳功率曲線 Popt。

由功率函數表達式可知，風力機功率值在特定風速值下與風能利用系數有關，使風能利用系數Cp取得最大值十分關鍵。圖2(b)所示即為槳距變化情況下，風能利用系數與葉尖速比的關系。在特定槳距角下，存在唯一最佳葉尖速比λopt使得風能利用系數達到最佳值CPmax，但是根據Betz極限［7］，風能利用系數上限值約為0.593，實際中Cp還要更小，現代商用風力機能達到的風能利用系數值約為0.45。

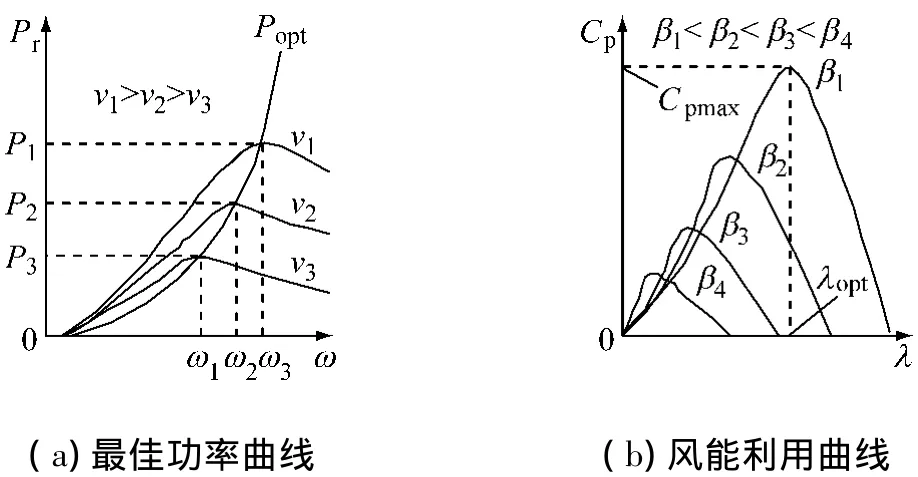
圖2 風力機特性曲線

風機轉速ω的調節有兩種方式［7］:風力機槳葉變節距調節和控制發電機輸出功率調節。變節距調節時風速難以檢測、精度低、系統復雜，因此多采用功率調節方式使轉速變化。

與異步電機矢量控制不同的是，雙饋發電機的最終控制目的不是轉速，而是對功率的有效控制。在風速變化情況下，由風速、葉尖速比、發電機轉速實時計算得出風功率、風能利用系數，并使實時捕獲到的有效機械功率作為有功功率參考值。利用反饋參數，通過閉環控制，產生PWM脈沖波控制開關器件工作，調節發電機實際功率值，間接使發電機功率跟蹤風速的變化，使風力機運行于最佳功率曲線上，獲取最大風能。

3 雙饋電機及轉子側PWM變換器控制

3.1 雙饋電機數學模型

首先需要建立雙饋電機數學模型，在建立模型之前，先作如下假設［6］:

(1)定子繞組為三相對稱繞組;

(2)氣隙磁場在空間為正弦分布，磁場的高次諧波忽略不計;

(3)電機的磁路為線性，鐵心中的磁滯損耗和渦流損耗忽略不計;

(4)定子側取發電機慣例，電流以流出方向為正，正向電流產生負值磁鏈;轉子側取電動機慣例，電流以流入方向為正，正向電流產生正值磁鏈。

則在d-q同步速旋轉坐標系下，雙饋發電機的等效電路如圖3所示［8］。

圖3 雙饋電機dq等效電路模型

寫成數學表達式即為

定轉子電壓方程:

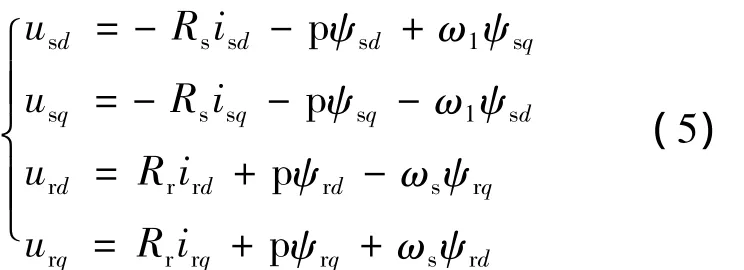
定轉子磁鏈方程:

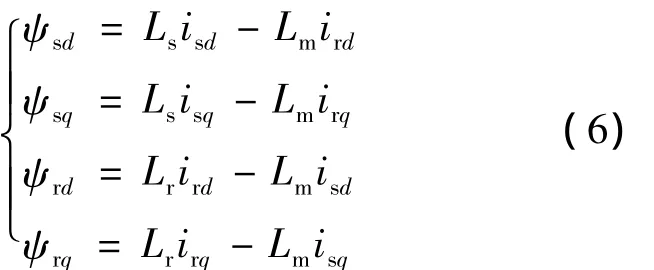
電磁轉矩與運動方程為

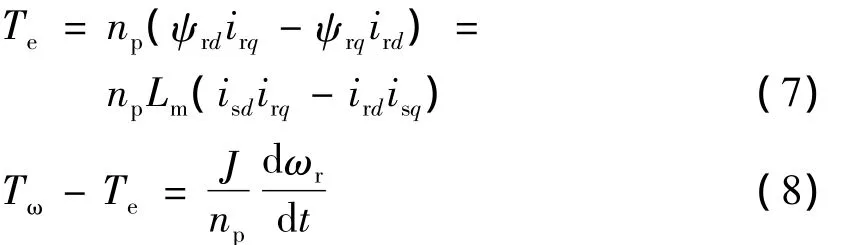
式中:ω1——同步旋轉角頻率，ωs= ω1－ ωr表示轉差角頻率;

p——微分算子d/dt;

np——電機極對數;

Rs、Rr——定、轉子電阻值;

Ls、Lr、Lm——定、轉子電感，定轉子間互感。

3.2 PWM變換器矢量控制設計

采用定子磁鏈定向，可以使矢量控制模型得到簡化。將定子磁鏈矢量定向于d軸上，則有:ψsd=ψs，ψsq=0，定轉子坐標變換關系如圖 4 所示。d-q坐標軸表示以同步速ω1旋轉的坐標系;αs-βs表示兩相定子坐標系(靜止)，αr-βr表示兩相轉子坐標系，以轉子角速度ωr旋轉。αs與αr間的夾角為θr，αs與d軸間的夾角為θs。由于定子與電網直接相連，其上的頻率為工頻，與定子電抗相比較，定子繞組電阻可以忽略不計，即Rs=0，可認為定子電壓us與感應電勢e一致，且滯后于定子磁鏈90°，即有定向條件:

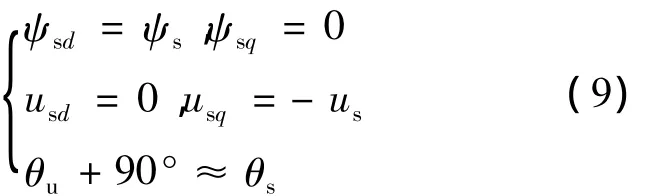
將以上定向條件代入電壓，磁鏈及功率方程中整理可得:

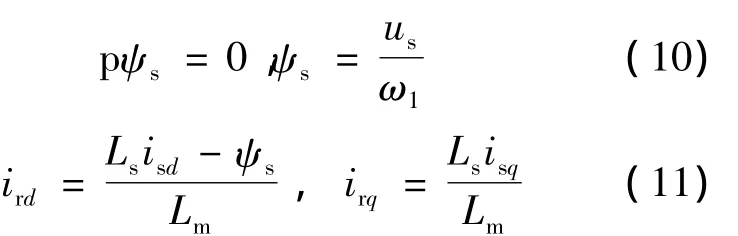
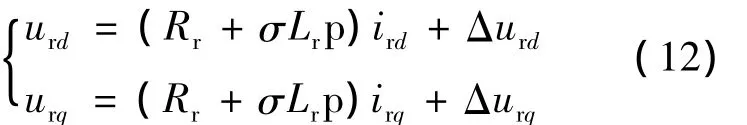
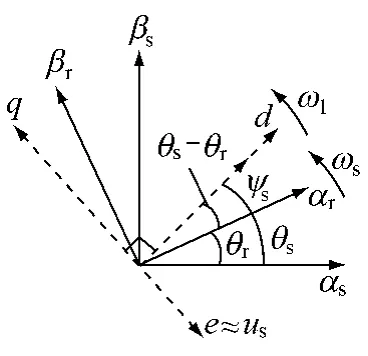
圖4 定轉子矢量坐標關系

Δurd，Δurq表示轉子電壓補償量:

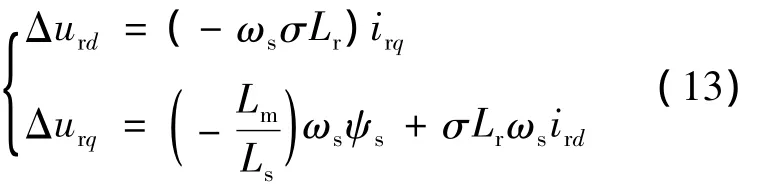
根據定子側功率方程:

由上可知:

(1)定子磁鏈定向下，磁鏈值可以表示成定子電壓與定子角頻率的比值形式;

(2)us恒定，有功功率、無功功率分別與定子電流的q軸分量和d軸分量成正比，調節這兩個分量，便可實現對功率的調節;

(3)結合轉子電壓補償量，對轉子電流進行閉環控制，便可實現對轉子電壓的調節。

按此關系可以設計出轉子側變換器前饋解耦控制器，寫成函數表達式形式為:

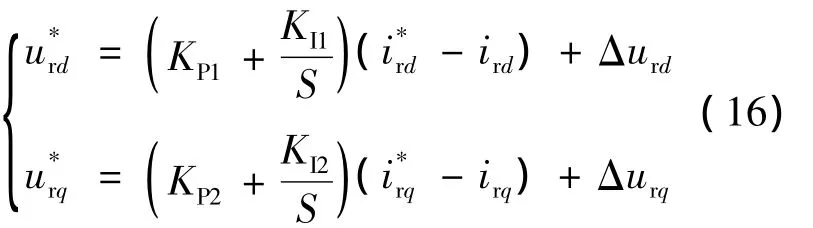
根據對磁鏈矢量的計算方式及其對控制效果的影響對比研究［9］，如果按照求取定子αβ軸上磁鏈分量，取正切值的方法，功率值將會產生震蕩比較大的影響。因此，可按式(10)得出，其實現原理如圖5所示。

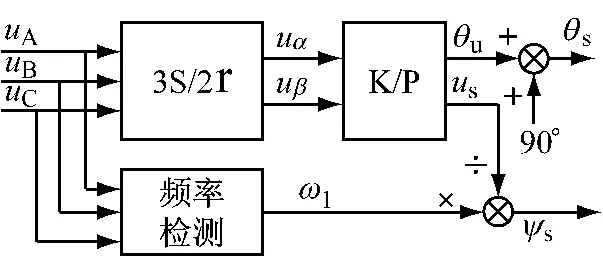
圖5 定子磁鏈計算模型

按照以上推導過程，可建立定子磁場定向的雙饋風力發電控制模型如圖6所示。

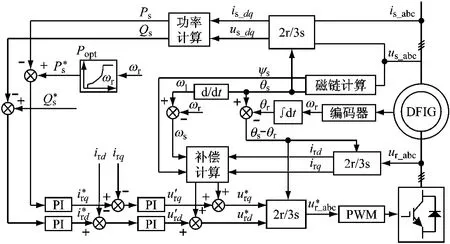
圖6 定子磁鏈定向矢量控制結構圖

4 仿真試驗及分析

為驗證此控制策略的有效性，在MATLAB/Simulink上進行了仿真研究，仿真所用部分參數如表1所示。取直流側電容C=104μF，直流電壓值設定為 Udc=1 200 V，CPmax=0.432，λ =8.1。首先進行功率解耦控制，然后在風速變化情況下，對發電機跟隨風能變化情況進行研究。

風速恒定情況下，一組在0 s時刻設定有功功率初始值為 0.3 p.u.，1 s時躍升為 0.5 p.u.，2 s時突減至 0.3 p.u.，無功功率值設定為 0 p.u.不變;另一組設定有功功率為0.3 p.u.不變，無功功率由 0 p.u.變為 － 0.3 p.u.，再變回 0 p.u.。圖7所示為上下兩組仿真結果，對有功功率和無功功率的調節過程是相對獨立的，顯示了該系統具有良好的功率解耦控制性能。

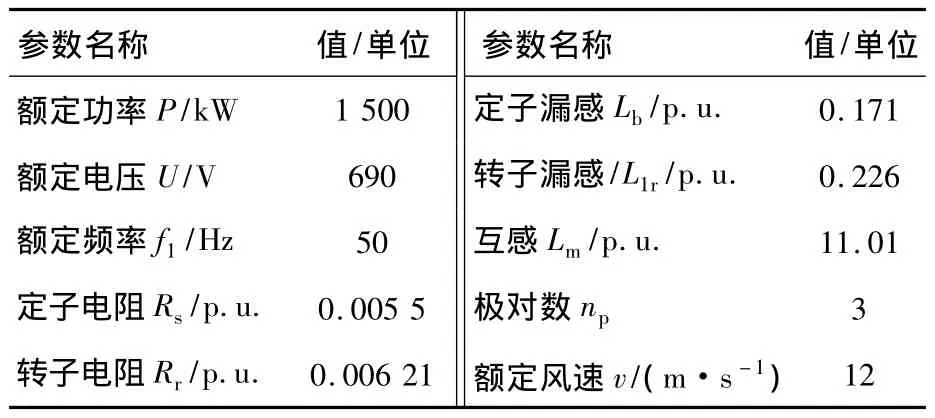
表1 仿真用DFIG參數表

當給定風速初始值設定為7 m/s，1 s時躍升至8.5 m/s，2 s時使風速按照一定斜率下降，3 s時恢復為7 m/s。如圖8(a)為給定風速變化曲線，8(b)為功率變化曲線。當風速發生變化時，發電機能夠自動跟蹤風能，且響應速度較快。

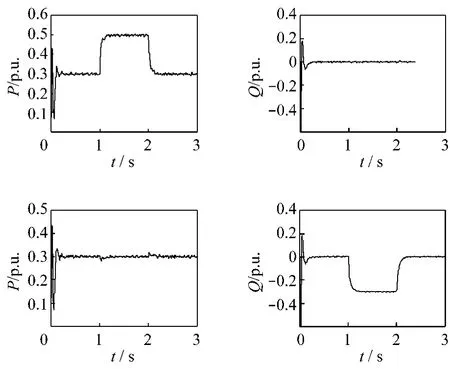
圖7 有功、無功功率解耦控制

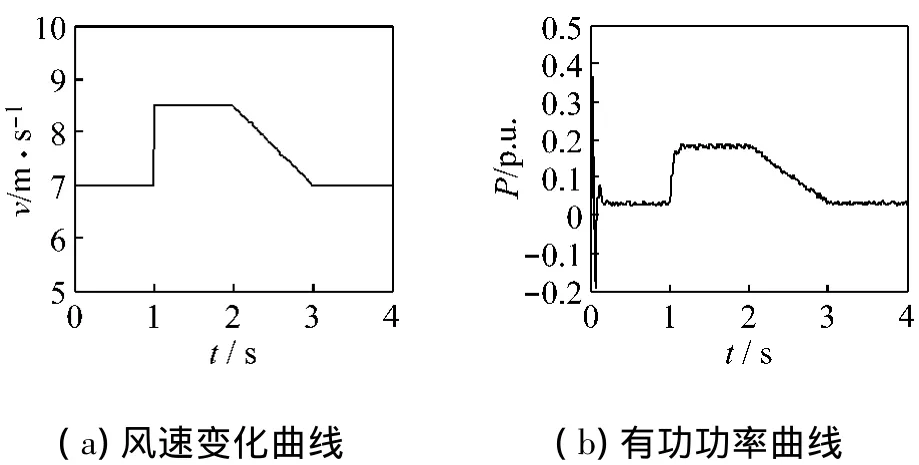
圖8 發電機有功功率跟隨風速變化

圖9為直流母線電壓、風速變化，其值基本上能夠保持1 200 V恒定不變。圖10為定子側相電壓與相電流波形圖，當風速發生變化，波形能夠平穩過渡，除了相電流幅值發生變化，二者間的相位關系依然為反相，從而實現變速恒頻的發電過程，說明該控制系統具有良好的穩定性。

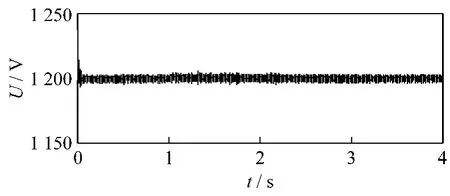
圖9 直流側電壓

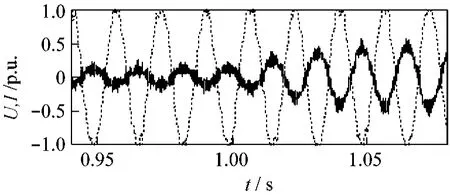
圖10 定子側相電壓相電流曲線

5 結 語

介紹了雙饋風力發電機的數學模型，風力機工作特性曲線。從轉子側變換器著手，對其實現有功功率、無功功率解耦控制，以及最大風能捕獲的原理進行分析。通過采用功率外環電流內環的定子磁鏈定向的控制策略使功率得到解耦，使用功率調節方式使風力機始終運行在最佳功率曲線上，從而捕獲最大風能。通過搭建雙PWM變換器控制系統的仿真模型，驗證了該控制模型在雙饋風力發電系統上具有良好的性能。但該系統是在理想電網下建立的模型，如果電網條件發生變化，尤其是不對稱故障情況下，尚需進一步探索。

［1］郭小明.電網異常條件下雙饋異步風力發電機的直接功率控制［D］.浙江大學博士學位論文，2008.

［2］Pena R，Clare J C，Asher G M.Double fed induction generator using back-to-back PWM converters and its application to variable-speed wind-energy generation［J］.Electric Power Applications，IEE Proceedings，1996，143(3):231-241.

［3］Tapia A，Tapia G，Ostolaza J X，et al.Modeling and control of a wind turbine driven doubly fed induction generator［J］.IEEE Transactions on Energy Conversion，2003，18(2):194-204.

［4］劉其輝，賀益康，張建華.交流勵磁變速恒頻風力發電機的運行控制及建模仿真［J］.中國電機工程學報，2006，26(5):43-50.

［5］Fernando D Bianchi，Hernan De Battista，Ricardo J Mantz.Wind turbine control systems［M］.2007.

［6］湯蘊璆，張奕黃，范瑜.交流電機動態分析［M］.北京:機械工業出版社，2008.

［7］顧軍，葉滿園.雙饋風力發電系統中有功無功解耦控制技術的仿真研究［J］.防爆電機，2006，41(4):25-28.

［8］陳伯時，陳敏遜.交流調速系統［M］.北京:機械工業出版社，2006.

［9］Shuhui Li，Challoo R，Nemmers M J.Comparative study of DFIG power control using stator-voltage and stator-flux oriented frames［C］∥IEEE Power＆ Energy Society General Meeting，2009(7)1-8.