高強(qiáng)鋼絞線網(wǎng)加固RC梁抗剪性能及計算方法

黃華 ，劉伯權(quán)，吳濤

(1. 長安大學(xué) 建筑工程學(xué)院，陜西 西安，710061；2. 長安大學(xué) 舊橋檢測與加固技術(shù)交通行業(yè)重點實驗室，陜西 西安，710064)

近年來，高強(qiáng)不銹鋼絞線網(wǎng)-滲透性聚合物砂漿加固技術(shù)在國內(nèi)外得到越來越廣泛的使用，比較典型的有北京市方興賓館樓板加固工程、中國美術(shù)館加固改造工程以及河北滄州東關(guān)大橋加固工程等。對該加固技術(shù)的研究主要集中在抗彎加固方面[1-4]，而對抗剪加固方面所進(jìn)行的研究較少，各種試驗資料相對缺乏，已有研究[5-6]考慮的影響因素不夠全面，加固設(shè)計、施工規(guī)范尚不完善。在此，本文作者通過9根鋼筋混凝土矩形梁的抗剪加固試驗和 12根鋼筋混凝土矩形梁的抗剪加固數(shù)值計算，分析加固梁抗剪破壞機(jī)理，探討混凝土強(qiáng)度、鋼絞線用量、持載程度、加固方式、配箍率、螺栓的數(shù)量和間距、剪跨比等對加固性能的影響，提出相關(guān)加固設(shè)計計算公式。

1 抗剪加固試驗

抗剪加固試驗共制作9根鋼筋混凝土矩形梁，尺寸及配筋如圖1所示。混凝土強(qiáng)度為48.45 MPa；箍筋直徑為6 mm，屈服強(qiáng)度為353.63 MPa，極限強(qiáng)度為524.88 MPa；縱筋直徑為22 mm，屈服強(qiáng)度為452.63 MPa，極限強(qiáng)度為619.30 MPa；加固用高強(qiáng)鋼絞線直徑為3.2 mm，極限強(qiáng)度為1 606 MPa。試驗梁加固方案如圖2所示，編號及分類見表1。表1中：RCBS-1~5號構(gòu)件為一次受力構(gòu)件，加固前未加載；RCBS-6~8為二次受力構(gòu)件，6號和7號分別加載至對比梁極限荷載的48%和58%時，進(jìn)行持載加固，8號則加載至極限荷載后完全卸載，并進(jìn)行修復(fù)加固。

圖1 加固梁截面尺寸及配筋(單位：mm)Fig.1 Profile and reinforcement of cross section

圖2 加固示意圖(單位：mm)Fig.2 Strengthening design of specimens

加固構(gòu)件剪力-撓度曲線見圖3，主要試驗結(jié)果見表2。由圖3及表2可見，加固后各梁的特征荷載均得到了不同程度的提高，梁抗剪加固的效果非常顯著；鋼絞線固定用膨脹螺栓的數(shù)量對加固承載力有明顯影響，螺栓過多、間距過小時會對原梁造成較大損傷；持載48%的加固梁與完整加固梁承載力相差不大，但持載程度 58%的加固梁承載力提高幅度明顯減小；2號環(huán)包加固梁承載力提高幅度明顯比U形加固梁的提高幅度低；8號環(huán)包加固的修復(fù)梁屈服承載力提高幅度與U形加固梁的相當(dāng)，但極限承載力提高幅度較低。

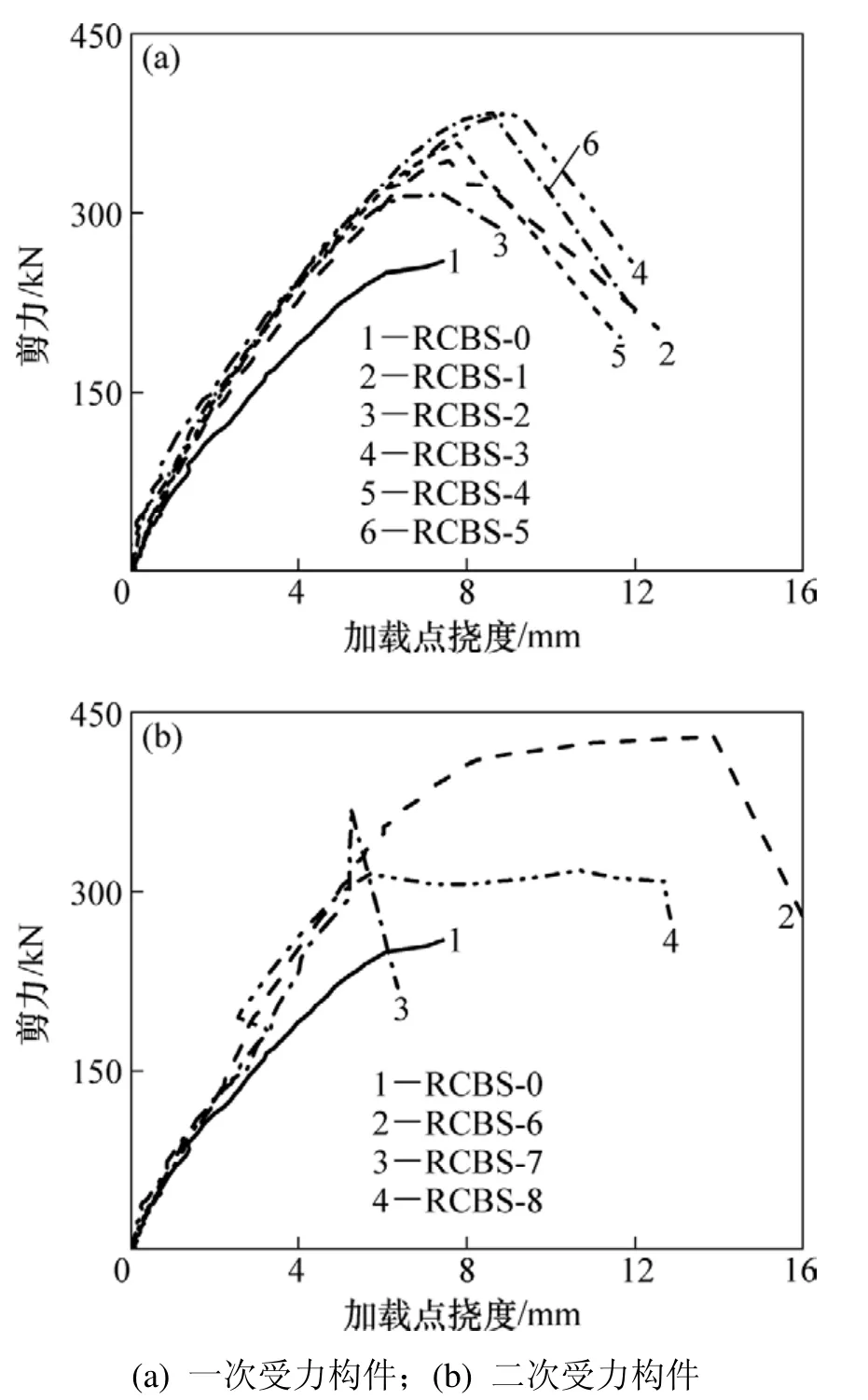
圖3 剪力-撓度曲線Fig.3 Shear capacity-deflection curves

表1 加固試件編號及分類Table 1 Number and sort of strengthened beams

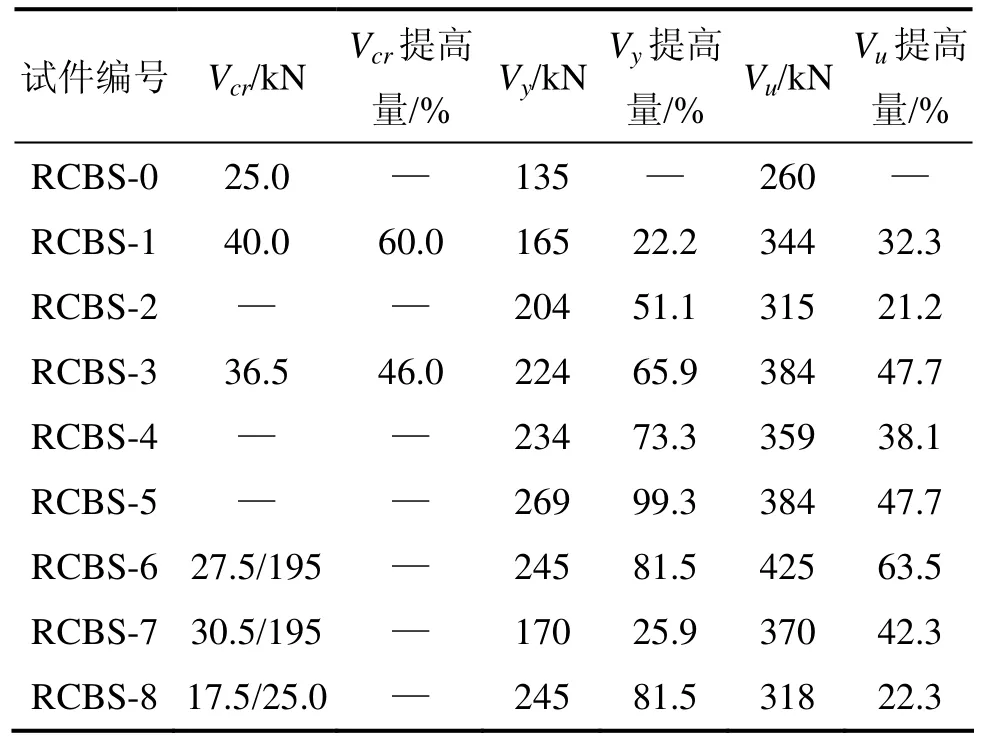
表2 主要試驗結(jié)果Table 2 Main test results

典型的破壞模式如圖4所示，構(gòu)件最終均發(fā)生加固層剝離破壞，在剝離的瞬間，荷載全部傳遞給壓區(qū)混凝土，構(gòu)件瞬間剪切破壞而喪失承載力。持載加固梁與完整加固梁相比，前者發(fā)生剝離破壞的突然性較后者的更大，脆性破壞更強(qiáng)烈；U形加固梁與環(huán)包加固梁相比，前者直接在梁頂產(chǎn)生層間裂縫而發(fā)展成剝離，后者沿頂部和底部砂漿層出現(xiàn)水平貫通裂縫，然后發(fā)展為剝離。

圖4 加固梁破壞形態(tài)圖Fig.4 Failure mode of strengthened beam

2 抗剪加固數(shù)值分析

2.1 有限元試驗驗證

基于以上試驗，利用有限元程序ANSYS，建立數(shù)值模型，分析混凝土強(qiáng)度、配筋率、鋼絞線用量、加固方式、剪跨比等對抗剪性能的影響。混凝土采用Soild65單元和Willian-Warnke五參數(shù)破壞準(zhǔn)則確定，單軸抗壓應(yīng)力-應(yīng)變曲線采用Hongnestad模型確定；鋼筋采用 Link8單元和雙線性隨動強(qiáng)化模型(KINH)確定，應(yīng)力-應(yīng)變曲線采用彈塑性強(qiáng)化模型確定；對于加固層的剝離，則通過文獻(xiàn)[7]描述的黏結(jié)-滑移本構(gòu)關(guān)系來考慮[8-11]。

有限元計算與試驗所得剪力-撓度對比曲線見圖5。圖中 FEMS-48為有限元計算曲線，RCBS-3~5為試驗曲線。其中，有限元計算的極限荷載與試驗均值的差值為 0.74%，撓度的差值為 3.89%，表明有限元計算結(jié)論正確，可用于加固梁的參數(shù)分析。

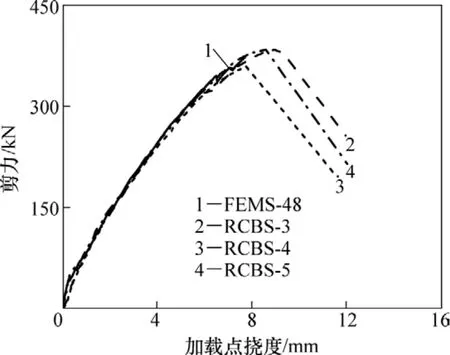
圖5 剪力-撓度對比曲線Fig.5 Shear capacity-deflection contrast curves

2.2 加固梁參數(shù)分析

抗剪加固梁參數(shù)分析主要考慮以下幾種因素：混凝土強(qiáng)度、配箍率、鋼絞線用量、剪跨比和加固方式。計算結(jié)果見表4。由表4可見：混凝土強(qiáng)度和配箍率對抗剪加固梁受力性能有非常大的影響，隨混凝土強(qiáng)度和配箍率提高，極限承載力提高，但鋼絞線利用率前者提高而后者降低；無論是U形加固還是環(huán)包加固，隨鋼絞線用量的增加，構(gòu)件極限承載力均提高，但后者提高幅度要遠(yuǎn)大于前者的提高幅度；隨鋼絞線用量增加，其利用率降低，但環(huán)包加固的鋼絞線利用率較高；隨剪跨比增大，主拉應(yīng)力對破壞的貢獻(xiàn)越來越大，抗剪承載力和鋼絞線的利用率均逐步降低。

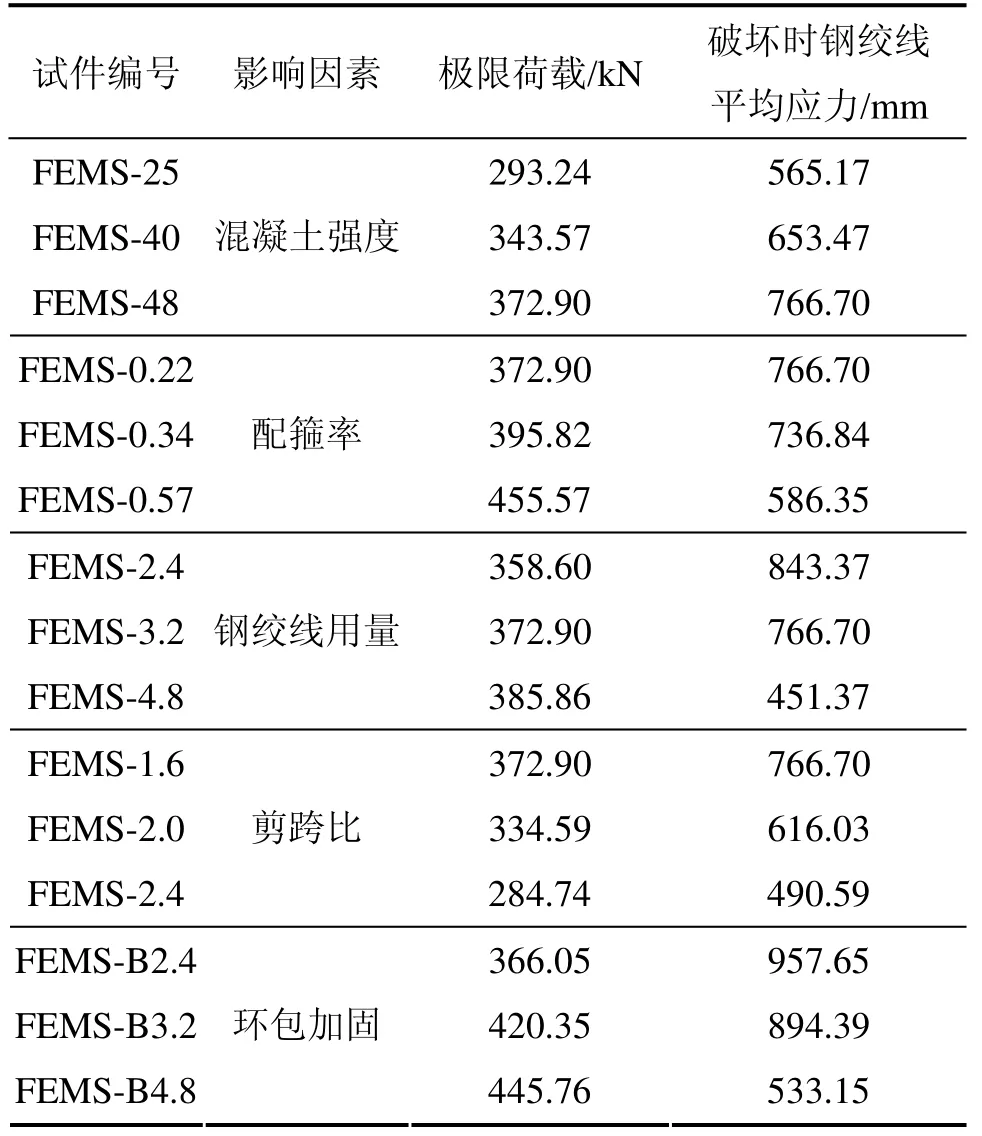
表4 抗剪加固梁數(shù)值計算結(jié)果Table 4 Numerical analysis results of shear strengthened beams

3 抗剪加固計算公式

3.1 抗剪加固理論分析

加固后的鋼筋混凝土梁抗剪承載力主要成分由下列幾部分組成：斜裂縫上端、靠梁頂部未開裂混凝土的抗剪力Vc，沿斜裂縫的混凝土骨料咬合作用Vi，縱筋的橫向(銷栓)力Vd，箍筋和彎起鋼筋的抗剪力Vsv、Vb，加固聚合物砂漿的抗剪力Vm，加固高強(qiáng)鋼絞線的抗剪力Vsw等，加固梁斜截面抗變力作用示意圖如圖6所示。這些抗剪成分的作用和相對比例，在構(gòu)件的不同受力階段隨裂縫的形成和發(fā)展而不斷地變化。構(gòu)件極限狀態(tài)的抗剪承載力為這幾部分的總和：

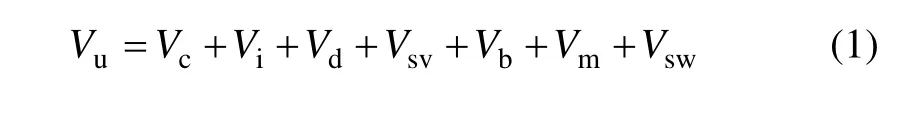
加固梁的主要抗剪成分所承擔(dān)的剪力比例，取決于混凝土的強(qiáng)度、腹筋、縱筋、彎起鋼筋、聚合物砂漿、高強(qiáng)鋼絞線的數(shù)量和布置方式等因素，在各受力階段不斷地發(fā)生變化。而且荷載的位置(剪跨比)對梁的破壞形態(tài)也有很大影響。

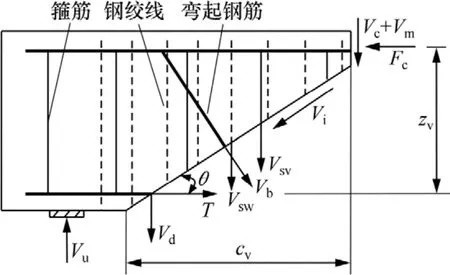
圖6 加固梁斜截面抗剪作用Fig.6 Shear resistance of oblique section of strengthened beam

3.2 加固層抗剪能力計算

高強(qiáng)鋼絞線網(wǎng)-聚合物砂漿抗剪加固承載力設(shè)計主要需解決加固部分的抗剪承載力。眾多對粘貼FRP抗剪加固的研究[12-14]也是在原梁抗剪承載力基礎(chǔ)上，考慮 FRP材料對抗剪承載力的貢獻(xiàn)。令高強(qiáng)鋼絞線網(wǎng)-聚合物砂漿加固層對抗剪承載力的貢獻(xiàn)為：

式中：Vmw為加固層的抗剪承載力；Vm為加固聚合物砂漿的抗剪承載力；Vsw為加固高強(qiáng)鋼絞線的抗剪承載力，分別由式(3)和(4)計算。

式中：β1為加固方式影響系數(shù)；η2為加固體與本體梁之間共同工作系數(shù)，U形加固取值為0.9，環(huán)包加固在此基礎(chǔ)上提高0.1；η1為鋼絞線應(yīng)力發(fā)揮綜合系數(shù)，由于抗剪加固基本上發(fā)生剝離破壞，故其取值與抗彎加固[15]有所差別。

對加固方式影響系數(shù)β1，根據(jù)表4中抗剪加固破壞時高強(qiáng)鋼絞線的平均應(yīng)力，環(huán)包加固時，β1=1.15；U形加固時，β1=1.0。

對鋼絞線應(yīng)力發(fā)揮綜合系數(shù)η1，由表4中數(shù)據(jù)分析可見，其與混凝土立方體抗壓強(qiáng)度、鋼絞線直徑、剪跨比均有聯(lián)系，而原梁配箍率的影響不大，故此處不考慮其影響。η1可由下式表示：

式中：αfcu為混凝土立方體抗壓強(qiáng)度影響系數(shù)；αd為鋼絞線直徑影響系數(shù)；αλ為剪跨比影響系數(shù)，這些影響因素與應(yīng)力的關(guān)系見圖7。圖中擬合曲線分別為：

αλ= 0 . 9 6-0.25λ (相關(guān)系數(shù)為0.999)

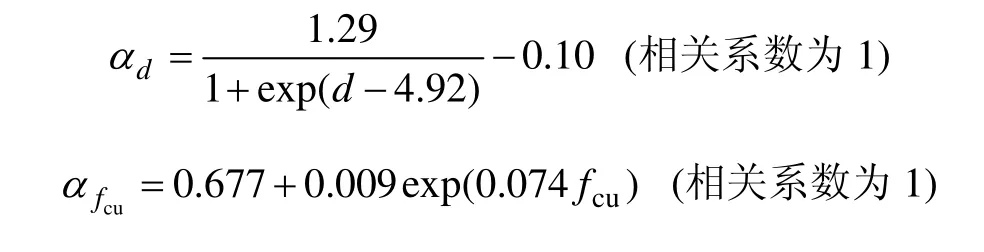
從而可得鋼絞線應(yīng)力發(fā)揮綜合系數(shù)η1的公式為：

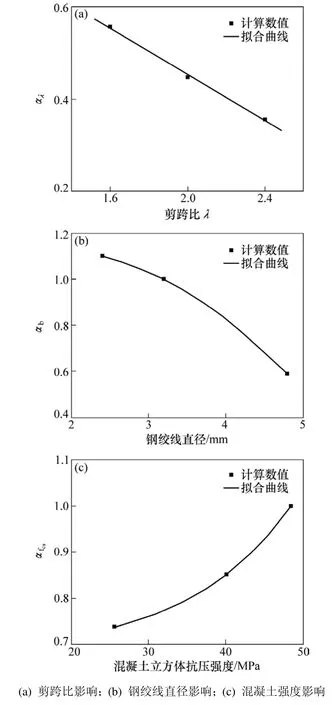
圖7 鋼絞線應(yīng)力發(fā)揮綜合系數(shù)影響因素關(guān)系Fig.7 Relationship between stress of stainless steel wire and its influencing factors

聚合物砂漿及高強(qiáng)鋼絞線的有效高度hsm和hsw取值如圖8所示。其中：hz為加固層頂面至梁頂面的距離；dz為鋼絞線頂端至砂漿層頂面距離；h為梁高；hf’為翼緣高度；h0為鋼筋有效高度；tm為加固層厚度。

對U形加固，由圖5(a)可得如下關(guān)系：

當(dāng)翼緣高度為0時，T形梁轉(zhuǎn)化為矩形梁，則有hsm=h0；當(dāng)dz=0時，有hsm=hsw=h0。

對環(huán)包加固，由圖7(b)可得如下關(guān)系：hsm= h0+tm；對于hsw，與hsm略有差異，可近似認(rèn)為hsw= hsm。

3.3 加固構(gòu)件抗剪承載力計算

在式(2)基礎(chǔ)上根據(jù)現(xiàn)行規(guī)范，建立加固構(gòu)件抗剪承載力計算公式。

對《公路鋼筋混凝土及預(yù)應(yīng)力混凝土橋涵設(shè)計規(guī)范》JTG D62-2004(以下簡稱《公路橋規(guī)》)而言，受彎構(gòu)件斜截面抗剪承載力計算如下：

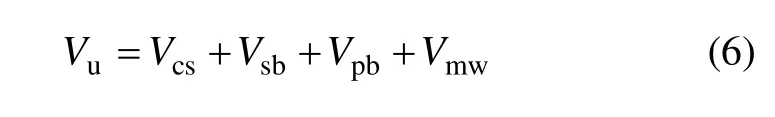
式中：Vu為構(gòu)件極限抗剪承載力；Vcs為斜截面內(nèi)混凝土和箍筋共同的抗剪承載力；Vsb為與斜截面相交的普通彎起鋼筋抗剪承載力；Vpb為與斜截面相交的預(yù)應(yīng)力彎起鋼筋抗剪承載力；具體計算參見《公路橋規(guī)》。

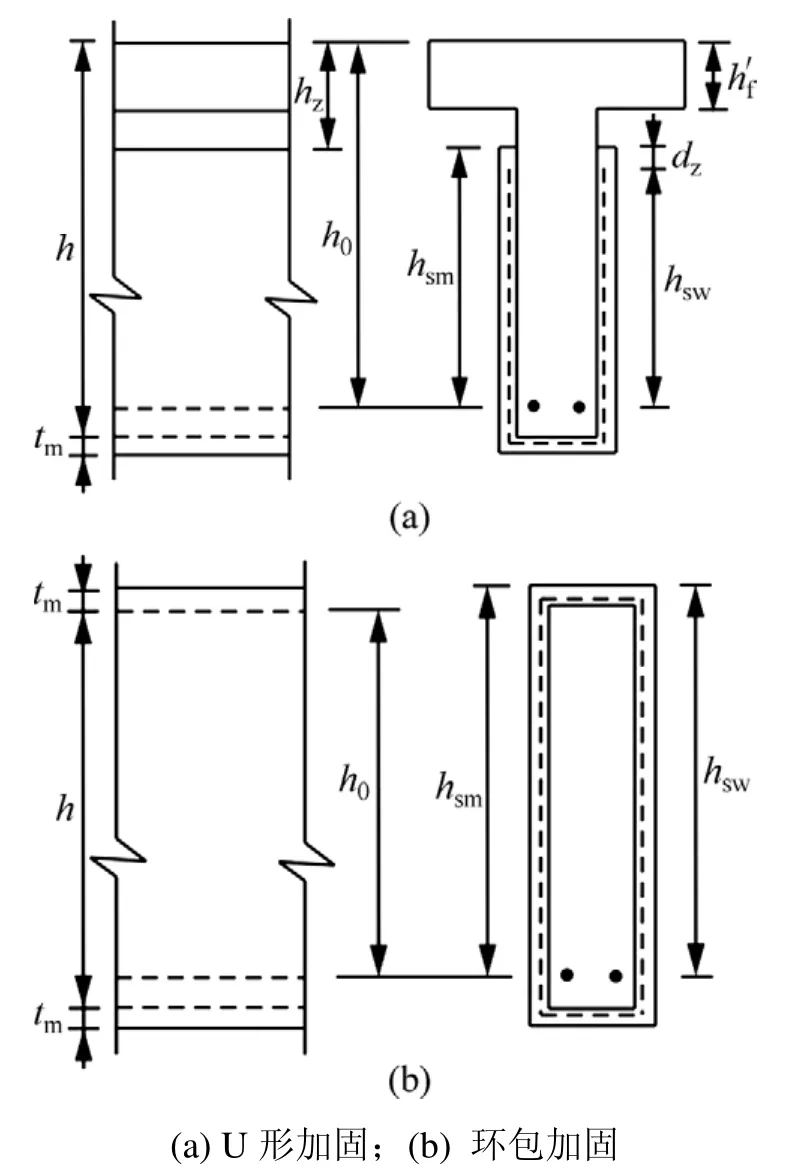
圖8 加固層有效高度取值Fig.8 Value of effective highness of reinforced layer

對于《混凝土結(jié)構(gòu)設(shè)計規(guī)范》GB 50010-2010(以下簡稱《混凝土規(guī)范》)，受彎構(gòu)件斜截面抗剪承載力計算如下：

式中：Vp為預(yù)加力所提高的構(gòu)件抗剪承載力；0.8fyAsbsinαs為與斜截面相交的普通彎起鋼筋抗剪承載力；0.8fpyApbsinαp與斜截面相交的預(yù)應(yīng)力彎起鋼筋抗剪承載力。具體計算參見《混凝土規(guī)范》。

式(2)，(6)和(7)計算值與試驗值對比見表 5。對Vmw，計算值與試驗值和數(shù)值試驗值比值的均值為0.973，方差為0.108，離散系數(shù)為0.111，由此可見：公式計算加固層提供的抗剪承載力是符合實際的，與試驗結(jié)果較符合，公式計算值偏于安全。式(6)按《公路橋規(guī)》計算值與試驗值和數(shù)值計算值比值的均值為0.719，方差為0.046，離散系數(shù)為0.064，由此可見：公式計算加固梁抗剪承載力是符合橋梁實際的，公式計算值偏于安全，試驗值是計算值的1.39倍，已具備較高的安全儲備。如需達(dá)到更高的安全儲備，可將共同工作系數(shù)η2取0.7或更低的值。式(7)按《混凝土規(guī)范》計算值與試驗值和數(shù)值計算值比值的均值為0.928，方差為0.039，離散系數(shù)為0.042，表明計算值與試驗值較符合，公式計算值偏于安全，已具備一定的安全儲備。

表5中試驗數(shù)據(jù)涵蓋了混凝土強(qiáng)度、原梁配箍率、加固鋼絞線用量、持載程度、剪跨比、加固方式等參數(shù)對加固的影響。式(6)和(7)具有較好的適應(yīng)性，可用于各自結(jié)構(gòu)的抗剪加固承載力設(shè)計。

此外，對原梁抗剪承載力損傷較為嚴(yán)重的梁抗剪加固承載力計算時，須對原梁的承載力進(jìn)行折減，此處引入原梁損傷系數(shù)ηd，式(6)和(7)變?yōu)槭?8)和(9)。

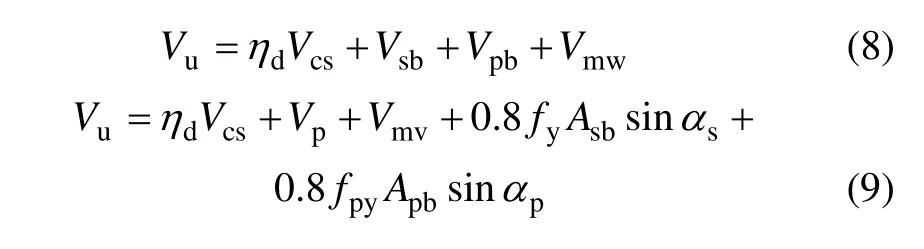
對于錨固高強(qiáng)鋼絞線網(wǎng)的螺栓過多造成的損傷，損傷系數(shù)ηd取 0.8；對于原梁損傷很大、箍筋已屈服的修復(fù)構(gòu)件如RCBS-8，損傷系數(shù)ηd取0.55或者更低的值；沒有損傷或損傷很小的構(gòu)件，損傷系數(shù)ηd取1.0。損傷梁加固抗剪承載力試驗值與計算值對比見表 6。由表6可見：計算結(jié)果有較大的安全儲備，公式可用于工程設(shè)計。

表5 抗剪加固梁計算值與試驗值對比Table 5 Comparison between calculation values and experimental results of shear strengthened beams

表6 損傷梁抗剪加固計算值與試驗值對比Table 6 Comparison between calculation values and experimental results of shear strengthened damaged beams

4 結(jié)論

(1) 高強(qiáng)鋼絞線網(wǎng)-聚合物砂漿抗剪加固效果顯著，梁抗剪承載能力得到了大幅度提高，裂縫發(fā)展得到了有效延遲。

(2) 鋼絞線網(wǎng)固定用螺栓數(shù)量對抗剪加固承載力有顯著影響，螺栓間距過密時，對梁斜截面造成較大損傷，承載力提高幅度比其他梁的提高幅度低1/3~1/2。

(3) 受多個方向的應(yīng)力復(fù)合作用，加固層最終發(fā)生剝離，混凝土壓碎而破壞。U形加固梁直接在梁頂產(chǎn)生層間裂縫而發(fā)展為剝離；環(huán)包加固梁沿頂部和底部砂漿層出現(xiàn)水平貫通裂縫，然后發(fā)展為剝離；后者延遲了剝離破壞的發(fā)生，對改善抗剪加固性能有很大作用。

(4) 持載加固與完整加固梁相比，破壞過程相似，但前者脆性破壞更加明顯；且持載程度對抗剪承載力有顯著影響，持載程度高，加固承載力提高幅度低，但修復(fù)加固梁效果顯著。

(5) 混凝土強(qiáng)度和配箍率對抗剪加固梁受力性能有非常大的影響，隨混凝土強(qiáng)度和配箍率提高，極限承載力提高，但前者的鋼絞線利用率提高而后者降低。

(6) 無論是U形加固還是環(huán)包加固，隨鋼絞線用量的增加，構(gòu)件極限承載力提高，而鋼絞線利用率降低，且后者承載力提高幅度及鋼絞線利用率均要比前者的大。

(7) 在試驗研究和理論分析的基礎(chǔ)上，提出抗剪加固承載力計算公式，可為工程實際提供參考。

[1] Ong K C G, Paramsivam P, Lim C T E. Flexural strengthening of reinforced concrete beams using ferrocement laminates[J].Journal of Ferrocement, 1992, 22(4): 331-342.

[2] Paramsivam P, Ong K C G, Lim C T E. Ferrocement laminates for strengthening RC T-beams[J]. Cement & Concrete Composites, 1994, 16(2): 143-152.

[3] 聶建國, 王寒冰, 張?zhí)焐? 等. 高強(qiáng)不銹鋼絞線網(wǎng)-滲透性聚合砂漿抗彎加固的試驗研究[J]. 建筑結(jié)構(gòu)學(xué)報, 2005, 26(2):1-9.NIE Jian-guo, WANG Han-bing, ZHANG Tian-shen, et al.Experimental study on flexural behavior of RC beams strengthened with stainless steel wire mesh and permeability polymer mortar[J]. Journal of Building Structures, 2005, 26(2):1-9.

[4] SHANG Shou-ping, ZENG Ling-hong, PENG Hui. Flexural strengthen of reinforced concrete beam with ferrocement[C]//Proceedings of the 28th Conference on All World in Concrete and Structures. Singapore, 2003: 28-29.

[5] 黃華, 劉伯權(quán), 劉衛(wèi)鐸. 高強(qiáng)鋼絞線網(wǎng)-聚合物砂漿抗剪加固梁二次受力試驗研究[J]. 工業(yè)建筑, 2009, 39(2): 99-102.HUANG Hua, LIU Bo-quan, LIU Wei-duo. Experimental study of shear behavior of RC beams strengthened with stainless steel wire mesh and polymer mortar under secondary load[J].Industrial Construction, 2009, 39(2): 99-102.

[6] 聶建國, 蔡奇, 張?zhí)焐? 等. 高強(qiáng)不銹鋼絞線網(wǎng)－滲透性聚合砂漿抗剪加固的試驗研究[J]. 建筑結(jié)構(gòu)學(xué)報, 2005, 26(2):10-17.NIE Jian-guo, CAI Qi, ZHANG Tian-shen, et al. Experimental study on shear behavior of RC beams strengthened with stainless steel wire mesh and permeability polymer mortar[J]. Journal of Building Structures, 2005, 26(2): 1-9.

[7] 黃華. 高強(qiáng)鋼絞線網(wǎng)-聚合物砂漿加固鋼筋混凝土梁式橋試驗研究與機(jī)理分析[D]. 西安: 長安大學(xué)建筑工程學(xué)院, 2008:63-68.HUANG Hua. Experimental study and theoretical analysis on strengthening RC girder bridge with steel wire mesh and polymer mortar[D]. Xi’an: Chang’an University. School of Civil Engineering,2008: 63-68.

[8] Padmarajaiah S K, Ramaswamy A. A finite element assessment of flexural strength of prestressed concrete beams with fiber reinforcement[J]. Cement & Concrete Composites, 2002, 24(2):229-241.

[9] 楊勇, 郭子雄, 聶建國, 等. 型鋼混凝土結(jié)構(gòu) ANSYS數(shù)值模擬技術(shù)研究[J]. 工程力學(xué), 2006, 27(4): 79-85.YANG Yong, GUO Zi-xiong, NIE Jian-guo, et al. Study on numerical simulation technology of steel reinforced concrete structures using ASNYS[J]. Engineering Mechanics, 2006, 27(4):79-85.

[10] 楊勇, 趙鴻鐵, 薛建陽, 等. 型鋼混凝土基準(zhǔn)粘結(jié)滑移本構(gòu)關(guān)系試驗研究[J]. 西安建筑科技大學(xué)學(xué)報: 自然科學(xué)版, 2005,37(4): 445-449.YANG Yong, ZHAO Hong-tie, XUE Jian-yang, et al.Experiment study on basic bond-slip constitutive relationship models between shaped-steel and concrete in SRC structures[J].Journal of Xi’an University of Architecture & Technology:Natural Science Edition, 2005, 37(4): 445-449.

[11] 江見鯨, 陸新征, 葉列平. 鋼筋混凝土結(jié)構(gòu)有限元分析[M].北京: 清華大學(xué)出版社, 2005: 44-176.JIANG Jian-jing, LU Xin-zheng, YE Lie-ping. Finite element analysis of concrete structures[M]. Beijing: Tsinghua University Press, 2005: 44-176.

[12] Arduini M. Parametric study of beams with externally bonded FRP reinforcement[J]. ACI Structure Journal, 1997, 94(5):465-482.

[13] Chen J F, Teng J G. Shear capacity of FRP strengthened RC beams: fiber reinforced polymer rupture[J]. Journal of Structural Engineering, 2003, 129(5): 615-625.

[14] Chen J F, Teng J G. Shear capacity of FRP strengthened RC beams: FRP debonding[J]. Construction and Building Materials,2003, 17(1): 27-41.

[15] 黃華, 劉伯權(quán), 邢國華, 等. 高強(qiáng)不銹鋼絞線網(wǎng)-滲透性聚合砂漿加固的 T型梁橋試驗[J]. 中國公路學(xué)報, 2007, 20(4):83-90.HUANG Hua, LIU Bo-quan, XING Guo-hua, et al. Experiment on RC T-type beam bridge strengthened with high strength stainless steel wire mesh and permeability polymer mortar[J].China Journal of Highway and Transport, 2007, 20(4): 83-90.