不同蟲態施用殺蟲劑對下一代昆蟲種群數量的影響

陶 杰，胡雅輝，賀淑嵐

（湖南省植物保護研究所，湖南 長沙 410125）

確定殺蟲劑的最佳施用時間是施藥技術中重要的一個環節，對控制害蟲有著重要的作用[1-6]。為了使殺蟲劑的效果最大化，這不僅需要知道害蟲種群的發生密度，也需要知道害蟲發生的蟲態，而大多數害蟲往往具備卵、幼蟲（或若蟲）、蛹（或偽蛹）和成蟲這幾個蟲態，在幼蟲期又根據蛻皮的次數分為不同的齡期。昆蟲對殺蟲劑的敏感性不但取決于殺蟲劑的種類，也取決于昆蟲的種類和蟲態[7]。長期以來，農民和研究者通常把昆蟲對殺蟲劑最敏感的發育時期作為最適施藥期。但是，根據害蟲綜合治理的原則[8]，施用殺蟲劑的主要目的是使下一代害蟲種群的數量降到最低，而不只局限在使當代害蟲種群的致死率最高。筆者提供的模型就是以這樣一種目的為前提，闡述如何判斷施用化學殺蟲劑的最佳時期。

1 模型定義

假如設定一種昆蟲有i=1～6個發育時期，包括卵、第一齡若蟲、第二齡若蟲、第三齡若蟲、偽蛹和成蟲。比如，黑刺粉虱 [Aleurocanthus spiniferus（Quaintance）]，假定越冬代的偽蛹數量（O）和凈增長率（R）。不同發育時期在田間的自然死亡率為Pi（i=1～6），不同發育時期施用殺蟲劑后的死亡率為Qi（i=1～6）。這樣，在沒有施用殺蟲劑的情況下，第一代偽蛹的種群數量（Y）應該可以表示為：

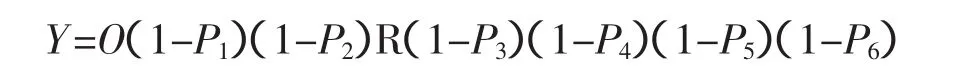
而只在昆蟲的第i個發育階段施用殺蟲劑的情況下，第一代偽蛹的種群數量（Yi）應該可以表示為：

要使防治效果最好，就應該使得第一代偽蛹的數量最小。在方程式（1）中Y是一個常數，令Ai=，則當 Ai最小時，Yi得到最小值 Ymin表示為如果一個參數或者一個函數式例如Qi、Pi、（Qi-P）i和Pi/Qi跟函數Ai有一一對應的關系，那么就可以通過這些參數或函數式代替Ai決定Ymin。很顯然，當Qi為常數，函數 Ai會隨著Pi的增大而增大，當 Pi為常數 ，Ai將隨著 Qi的增大而變小。因此，參數Qi或者Pi都跟Ai沒有一一對應的關系，不能代替Ai決定Ymin。假設（Qi－Pi）為常數 “b”（>0）,則當 Pi增大到 P1時，Qi也相應的增大到 Q1，公式表示為：b=Qi－Pi=Q1－P1。

如果 X1被定義為 X1=Q1－Qi=P1－Pi，那么：

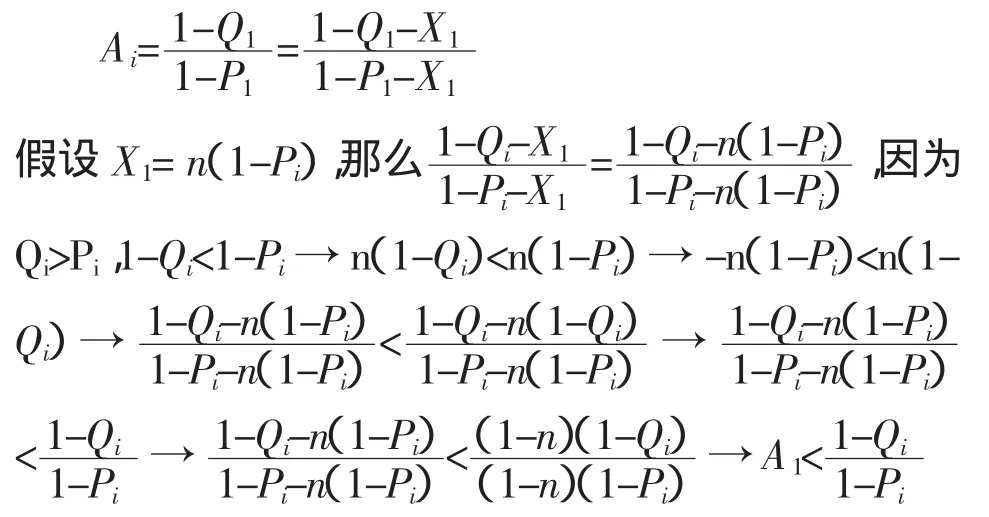
以上推導過程顯示，若（Qi－Pi）為常數b（b＞0），Ai將隨著Pi或Qi的增大而增大。因此，函數（Qi－Pi）跟Ai也不存在一一對應關系，即不可以通過該函數決定 Ymin。

假設函數 Pi/Qi是常數“c”（c＞0），則當 Pi增大到P2，那么 Qi也必須相應的增大到 Q2，即：c＝Pi/Qi＝P2/Q2和 P2/Pi＝Q2/Qi。如果 X2被定義為：X2=P2/Pi＝Q2/Qi，那么

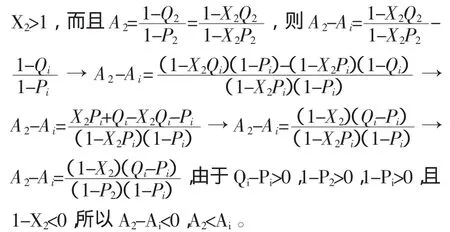
上述推導顯示 Pi/Qi為常數“c”（c＞0）時，Ai將隨著Pi或Qi的增大而減小。所以，函數Pi/Qi跟Ai也不存在一一對應關系，也不能通過Pi/Qi決定Ymin。簡而言之，參數Qi或Pi和函數（Qi－Pi）或Pi/Qi都跟Ai不存在一一對應關系，也就不能用來決定Ymin。同時，這些參數或函數中的任何兩個都可以一起被用來代替Ai決定Ymin，因為這些參數或函數中的任何兩個都可以組成一個具有唯一解的方程組。如果它們中的任何一個不變，則當Qi或（Qi－Pi）增大時，Ai減小；當Pi或Pi/Qi增大時，Ai也增大。

2 結果與分析

在許多殺蟲劑的生產應用試驗里，校正死亡率常被用來判定殺蟲效果，而校正死亡率的計數范圍往往只包括相鄰的兩個蟲態[9-11]。這樣判斷殺蟲劑的效果，在每個蟲態自然死亡率都一樣的情況下是可以的，但有其局限性，因為不同的發育階段會有不同的自然死亡率和不同的藥劑敏感性。筆者提出的模型中，函數Yi被用來判斷殺蟲劑的田間應用效果只考慮了一個完整的世代。應用該判斷標準可以很好地的解釋在筆者的試驗中，下一代黑刺粉虱種群密度減少最快的處理不是校正死亡率最大時施藥的處理（數據未列出）。

而一些參數或函數，如Qi、Pi、（Qi－Pi）或Pi/Qi被用來判斷最佳施藥時期（蟲態）的標準，也有他們各自的優點和局限性。函數Ai被用來判斷最佳施藥時期（蟲態）是很準確的，可是計算卻比較麻煩。有些昆蟲，只有特定的蟲態才容易被抽樣調查，此時也會采用自然死亡率（Pi）作為判斷最佳施藥時期（蟲態）的依據。有些藥劑，在田間對昆蟲特定的蟲態進行藥劑處理后，死亡率很高，此時，藥劑處理死亡率（Qi）也用來作為判斷最佳施藥時期（蟲態）的依據。而某些藥劑只對昆蟲的某個特定蟲態有作用，此時，校正死亡率（Qi－Pi）也被用作判斷最佳施藥時期（蟲態）的依據。自然死亡率和藥劑處理死亡率的比值 最接近Ai，可是，這個比值在試驗結果當中卻并不直觀。

許多生態模型都可以用來解釋試驗結果，但是這些模型在更進一步的外延時，大多會遇到這樣或那樣的問題。同樣的道理，方程式（1）也遇到了類似的問題，比如有些殺蟲劑對昆蟲害蟲的幾個世代都有持效作用，或者有些昆蟲的世代在田間呈現重疊的現象，這樣使用該模型作為判斷最佳施藥蟲態的標準也會出錯或者難以實施。

總之，筆者提供的模型可以作為判斷最佳施藥時期（蟲態）的方法。但是，當殺蟲劑施用之后的作用不僅對目前的蟲態有致死作用，而且對發育到后期的蟲態的死亡率也有影響，或者昆蟲世代嚴重重疊時，該模型還有待進一步的完善。

[1] 仇貴生，李美娜，張 平，等.蘋果主要病蟲害的預測預報、防治適期及藥劑選擇[J].中國植保導刊，2006，26（6）：31-33.

[2] 李學軍，王淑賢，鄭 國，等.遼寧朝陽地區高粱蚜田間消長規律及防治適期[J].昆蟲知識，2007，44（1）：53-57.

[3] 呂 欣，曾 琳，陸永躍，等.楊桃園桔小實蠅的防治適期研究[J].環境昆蟲學報，2008，30（3）：214-219.

[4] 劉守柱，杜學林，戴明勛.20%啶蟲脒對黃瓜蚜蟲的防治效果[J].湖南農業科學，2010，（3）：77-79.

[5] 楊少波，吳克桂.園藝場柑桔主要病蟲害發生及防治[J].廣東農業科學，2009，（7）：135-136.

[6] 龍亞芹，王萬東，王美存，等.云南小規模芒果種植模式和病蟲害防治調查[J].江西農業學報，2010，（11）：105-107.

[7] Nilima P，Castle S J，Toscano N C.Susceptibility of immature stages of Homalodisca coagulate （Hemiptera:Cicadellidae）to selected insecticides[J].Journal of Economic Entomology，2006，99（5）：1805-1812.

[8] Brown M W.Applying principles of community ecology to pest management in orchards[J].Agriculture,Ecosystems&Environment，1999，73（2）：103-106.

[9] 李 明，曾 唏，季祥彪，等.鹽酸黃連素對蚜蟲生物活性的研究[J].昆蟲學報，1999，42（2）：140-144.

[10] 蔣擁東，周芳芳，陳功錫.吉首寨陽大棚草莓病蟲害調查及防治措施[J].湖南農業科學，2010，（12）：90-91，95.

[11] Wang Y H，Gao C F，Xu Z P，et al.Buprofezin susceptibility survey,resistance selection and preliminary determination of the resistance mechanism in Nilaparvata lugens （Homoptera:Delphacidae） [J].Pest Management Science，2008，64（10）：1050-1056.