語義詞典歸類不當現象自動發現

邱立坤，邵艷秋

(1. 北京大學 計算語言學教育部重點實驗室，北京 100871； 2.北京城市學院 人工智能研究所，北京 100083)

1 引言

現有的語義詞典多數都是語言學工作者人工編制而成的，耗費了大量的人力和物力，但由于時間和精力的限制，不可避免的會存在義項缺失或義項不當的問題。《同義詞詞林》[1](以下簡稱《詞林》)最開始是為了寫作而編撰的，而且由于編制時間較早，義項設置的問題就更加嚴重。即使是像HowNet[2]這樣經過十余年時間編撰而成的詞典，也存在一定義項不當的問題。用人工的方式來改進現有的語義詞典是一件相當困難的工作，從數萬個詞語中尋找可能存在的義項缺失或義項不當問題就如大海撈針一般困難。一個比較現實的方法是使用自動計算方法來輔助發現缺失義項以及設置不當的義項。

本文工作的基礎是平行周遍原則。陳保亞[3]首次提出用平行周遍原則來區分詞和短語，之后又在文獻[4-5]中對此理論作了進一步的發展，認為所謂的“平行”指的是被替換的成分具有相同的特征，所謂的“周遍”指的是具有相同特征的成分在同樣的條件下都可以替換。比如，“老李、老張、老劉”符合“老+單音節姓氏”的規則，即平行又周遍，所有單音節姓氏都可以替換；“老虎、老鷹、老鼠”符合“老+單音節動物名”的規則，平行但不周遍，有許多反例，如“老羊”就不是一個合法的動物名。陳[3]認為符合平行周遍規則的詞語才應該收入詞典。本文將平行周遍規則與平行不周遍規則統稱為平行規則，這些規則在一定程度上反映了漢語詞語構詞模式上的規律性： 平行周遍規則比較嚴格，反例少，這一類規則的數量也比較少；平行不周遍規則比較寬松，反例多，這一類規則的數量比較多。

雖然陳保亞[3-5]所提出的平行周遍原則初衷在于區分詞和短語，但由于種種原因，現有的詞典在收詞時并沒有遵循這一原則，因此正如董秀芳[6]所述，現有詞典中的詞語既有不符合平行周遍原則的詞語(詞匯詞)，也有符合平行周遍原則的詞語(詞法詞)。因此，我們可以通過歸納的方法從詞典中自動地發現大量的平行規則。

平行規則的反例中有許多都是因為歸類不當所造成的，但也有許多歸類是正確的。如果單純依據平行規則的反例來發現歸類不當的現象，正確率太低；引入兩部詞典進行交叉驗證，可以明顯地提高正確率。因此本文的基本思路為：

給定兩部語義詞典，則可以歸納出兩套平行規則，每一套規則都有各自的正例和反例；如果一個詞典中某一規則的反例同時是另一個詞典中的正例，就意味著前一部詞典中的詞語可能屬于歸類不當。

本文剩余部分組織如下： 第2節簡要敘述相關工作；第3節對平行周遍原則進行具體化，分為雙向平行類推和成對替換類推兩類規則；第4節介紹兩類規則的自動獲取方法；第5節介紹基于兩類平行規則自動發現語義詞典歸類不當現象的算法；第6節給出本文的實驗結果；最后是結論。

2 相關工作

目前專門討論自動發現語義詞典歸類不當現象的文章很少，相關的工作主要集中于漢語未登錄詞語義類標注上。

K.Chen和C.Chen[7]提出了基于原型的模型。對于兩個具有相同核心字的詞語，該模型計算兩個詞語修飾成分的相似度作為兩個詞語的語義相似度。他們在一個包含200個名詞的集合上進行測試，所報告的精度達到了81%。

除了使用形態分析，Tseng[8]嘗試識別構成詞語的成分之間的形態句法關系。在為未登錄詞尋找一個最相似的詞語時，該方法首先要將形態句法關系不同的詞語過濾掉。這一方法的問題在于形態句法分類本身的難度尚在語義類猜測之上，因此不可避免地在一開始就產生許多的錯誤，從而導致最終的結果過低。這篇文章進行語義類猜測的目標集合僅包含《詞林》中最上層的12個大類。此粒度過粗，實用性不足，其所報告的精度與Lu[9]相比，也相差甚遠。

Lu[9]是目前漢語未登錄詞語義類判斷領域最有代表性的工作。其未登錄詞語義類判斷的方法與其詞類判斷的方法[10]比較類似，包括一個基于字類關聯的統計模型和一個基于規則的模型。其中，基于字類關聯的模型主要考慮出現于不同位置上的字與不同語義類之間的關聯強度，通過不同的算法來進行加權，最終得到一個較好的語義類判斷模型。基于規則的模型用于處理在詞典中可以找到結構類似詞語的未登錄詞，這些規則雖然只能處理少量的未登錄詞，但其正確率較高。兩者結合可以得到較好的效果(《詞林》第三級類上F值為61.6%，第二級類上為69.9%)。

上述相關研究表明，在進行漢語未登錄詞語義類標注時研究者主要使用成分結構特征，而上下文特征的有效性則有待于進一步的討論和驗證。本文所使用的平行原則本質上也屬于基于成分結構特征來判斷詞語的語義類。

3 平行周遍原則的具體化

將平行周遍原則運用到未登錄詞語義類標注中，首先要對之進行具體化，使之具備可操作性。本文將平行周遍原則具體化為兩種，分別是雙向平行類推規則與成對替換類推規則。

雙向平行類推的基本思想是： 一批語義類相同的成分{D1,D2…Dn}具有相同的構詞能力，它們分別與另一個成分A構成詞語{D1A,D2A…DnA}，且C(D1A)=C(D2A)…=C(DnA)。這里，C(DA)表示詞DA的語義類。例如，“保長、盟長、區長、省長、市長、縣長、鄉長、鄉鎮長、鎮長、州長”這一組詞具有一個共同字“長”，詞的整體義都屬于官員類，其中的替換成分則都屬于行政區劃類。

成對替換類推的基本思想是： 一對語義類相同的成分A、B具有相同的構詞能力，它們分別與另外一批成分{D1,D2，…，Dn}構成一批詞對{(D1A,D1B), (D2A,D2B)，…，(DnA,DnB)}，且C(D1A)=C(D1B), C(D2A)=C(D2B),…，C(DnA)=C(DnB)。例如，“分店、支店，分隊、支隊，分隊長、支隊長，分行、支行”這四對詞都有一對語義類相同的替換成分 “分、支”，每一對中的兩個詞語義類也相同。

4 雙向平行類推規則和成對替換類推規則自動抽取

4.1 雙向平行類推規則抽取

設詞典中存在一個詞語集合WS={D1A, D2A, …, DnA}，WS包含n個詞語，每個詞語DiA包含兩個成分“Di”和“A”，“Di”和“A”都包含一個或多個字。如果這n個詞語的語義類屬于同一個語義類，即C(D1A)=C(D2A) =… =C(DnA)，那么我們稱WS中的詞語整體語義類平行。根據這個集合，我們可以推導出一條規則： 給定一個未登錄詞Dn+1A，其語義類應為C(D1A)。我們稱這種規則為單向平行規則，稱Di為替換成分，A為共同成分。單向平行規則限制較小，因此會碰到過多的反例。

通過進一步加強限制，可以形成雙向平行類推規則。設詞典中存在一個詞語集合WS={D1A, D2A, …, DnA}，WS包含n個詞語，每個詞語DiA包含兩個成分“Di”和“A”，“Di”和“A”都包含一個或多個字。如果這n個詞語的語義類屬于同一個語義類，即C(D1A)=C(D2A) =… =C(DnA)，并且這n個詞語替換成分的語義類也屬于同一個語義類，即C(D1)=C(D2) =… =C(Dn)，那么我們稱WS中的詞語雙向平行。根據這個集合，可以推出一條規則： 給定一個未登錄詞Dn+1A，如果C(Dn+1)= C(D1)，則其語義類應為C(D1A)。此類規則可稱之為雙向平行類推規則，雙向平行分別指詞語語義類平行(相同)和替換成分語義類平行(相同)。一個雙向平行類推規則的條件可以表示為(A，C(w)，C(c))的三元組，其中A為共同成分，C(w)為詞語語義類，C(c)為替換成分語義類。

對于一個限制條件為(A，C(w)，C(c))的雙向平行類推規則Rj，Rj的正例應同時滿足詞語語義類平行條件和成分語義類平行條件；僅滿足成分語義類平行條件而不滿足詞語語義類平行條件的為反例，例如詞語BA滿足成分語義類平行條件，即C(B)=C(c)，但C(BA)≠C(w)，即不滿足詞語語義類平行條件，因此該詞語為Rj的反例；正例和反例詞語共同構成Rj的相關詞語集合Sj。

為了評估規則的可靠性，應設定兩個閾值： (1)正例的數量必須高于一定的閾值，設為λp；(2)正例在Sj中的比例必須高于一定閾值，設為λn。

考慮上述兩個因素，推導雙向平行類推規則的算法如下*要推導出所有雙向平行類推規則，需要遍歷所有可能的共同成分；對于每個共同成分對應的詞語集合，需要遍歷所有可能的詞語整體語義類和成分語義類。(以下稱算法1)：

(1) 給定一個語義詞典T和兩個閾值λp、λn；

(2) 獲得所有的構詞成分(構詞成分應該是T中的單字詞)；

(3) 初始化一個規則集合RS，置為空；

(4) 遍歷所有構詞成分：

a) 對于一個成分A，以A為共同成分，從T中抽取一個詞語集合WS={DiA| DiA∈T}；

b) 獲取WS中的替換成分語義類集合和詞語語義類集合，以枚舉的方式遍歷兩個語義類集合；

i. 設當前詞語語義類為CM1，替換成分Di語義類為CM2，以(A，CM1，CM2)為限制條件的規則記為Rj；

ii. 對于詞語DiA，如果C(Di)=CM2且C(DiA)=CM1，則DiA為Rj的正例，Rj的正例數(記為CountPj)加一；如果C(Di)=CM2且C(DiA)≠CM1，則DiA為相應規則的反例，將Rj的反例數(記為CountNj)加一；

(5) 遍歷規則集合RS

a) 給定規則Rj∈RS，限制條件為(A，CM1，CM2)；

b) 如果CountPj大于λp并且CountPj/(CountPj+CountNj)大于閾值λn，則可以產生一條雙向平行類推規則： 給定一個未登錄詞EA，如果C(E)=CM2，則C(EA)=CM1；否則不產生規則。

例如，給定共同成分 “市”和詞典《詞林》，詞語語義類為CM1=Di02，成分語義類為CM2=Cb25，則可找到正例121個，反例30個，正例比例為(121/(121+30))≈0.8。如果閾值λp、λn分別為3、0.5，則可以產生一條規則： 給定一個未登錄詞 “B市”，如果C(B)=Cb25，則C(B市)=Di02。

上面僅僅敘述了共同成分在后的情況，事實上，共同成分也可在前。兩種情況下推導雙向平行類推規則的過程是一致的，在此不再贅述。

4.2 成對替換類推規則抽取

一對語義類相同的成分A、B具有相同的構詞能力，它們分別與另外一批成分CS={D1,D2,…,Dn}構成一批詞對WPS={(D1A, D1B),(D2A,D2B),…,(DnA, DnB)}，且C(D1A)=C(D1B), C(D2A) =C(D2B),…,C(DnA)=C(DnB)。根據這條規則可以產生更多的新詞語，我們稱這種規則為成對替換類推規則，其中成對的成分A和B稱為共同成分對，與A和B構成詞的成分為替換成分。一個成對替換類推規則的條件可以表示為(A，B，C(A)=C(B)，C(DiA)=C(DiB))的三元組，其中A、B為共同成分對，A、B語義類相同(即成分語義類條件)，Di為替換成分，詞DiA和DiB語義類相同(即詞語語義類條件)。

對于一個限制條件為(A，B，C(A)=C(B)，C(DiA)=C(DiB))的規則Rj，Rj的正例應同時滿足詞語語義類條件和成分語義類條件；僅滿足成分語義類條件而不滿足詞語語義類條件的為反例，例如詞對(DiA，DiB)滿足成分語義類條件，即C(A)=C(B)，但C(DiA)≠C(DiB)，即不滿足詞語語義類條件，因此該詞語為Rj的反例；正例和反例詞語共同構成Rj的相關詞語集合Sj。

為了評估規則的可靠性，同樣應設定兩個閾值： (1)正例的數量必須高于一定的閾值，設為λp；(2)正例Sj中的比例必須高于一定閾值，設為λn。

推導成對替換類推規則的算法如下*要推導出所有雙向平行類推規則，需要遍歷所有可能的共同成分；對于每個共同成分對應的詞語集合，需要遍歷所有可能的詞語整體語義類和成分語義類。(以下稱算法2)：

給定一個語義詞典T和兩個閾值λp、λn；

(1) 找到所有的語義類相同的構詞成分對(構詞成分應該是T中的單字詞)；

(2) 初始化一個規則集合RS，置為空；

(3) 遍歷所有成分對：

a) 選擇一個語義類相同的成分對A、B(A和B通常是兩個字)，設兩個成分分別與另一個成分構成的詞對的集合為WPS={(D1A, D1B),(D2A,D2B),…,(DnA, DnB)}, 設以(A，B，C(A)=C(B)，C(DiA)=C(DiB))為限制條件的規則Rj；

i. 遍歷WPS的詞對WPi=(DiA，DiB)；

ii. 如果C(DiA)=C(DiB)，則WPi屬于Rj的一個正例，如果C(DiA)(C(DiB)，則WPi屬于Rj的一個反例，據此更新Rj的正例數CountPj和反例數CountNj；

b) 如果Rj的CountPj大于λp，且CountPj/(CountPj+CountNj)大于閾值λn，則可以推導出一條以(A，B，C(A)=C(B)，C(DiA)=C(DiB))為限制條件的成對替換類推規則： 對于未登錄詞w=DiA，如果T中存在詞語DiB，則C(DiA)=C(DiB)；對于未登錄詞w=DiB，如果T中存在詞語DiA，則C(DiB)=C(DiA)。

例如，給定具有相同語義類的替換成分對“部—局”和詞典《詞林》，閾值λn為0.5，在詞林中找到31對正例，14對反例，正例比例為31/(31+14)≈0.7，大于λn，因此可以產生一條成對替換規則： 對于未登錄詞w=E部，如果詞林中存在詞語E局，則C(E部)=C(E局)；對于未登錄詞w=E局，如果詞林中存在詞語E部，則C(E局)=C(E部)。

上面僅僅敘述了替換成分對在后的情況，事實上，替換成分對也可在前。兩種情況下推導成對替換類推規則的過程是一致的，在此不再贅述。

5 語義詞典歸類不當現象自動發現

5.1 詞典歸類結果類別劃分

在以人工方式對詞典歸類結果進行分類時，我們將之分為四類，分別是： 義項缺失，義項不當，其他不當，正確。六種類別中，義項缺失、義項不當、其他不當統稱為歸類不當。

所謂義項缺失指的是： 對于詞語w，詞典中已經為之標注了一個正確的義項S1，自動計算出的義項S2與S1不同，但也是一個正確的義項，因此，我們可以認為詞典缺少了義項S2。例如，在《詞林》中，“本鄉”應該有一個義項與“本村、本市”同類，但在《詞林》中沒有這個義項，這就屬于義項缺失。

所謂義項不當指的是： 對于詞語w，詞典中已經為之標注了一個義項S1，自動計算出的義項S2與S1不同，兩個義項相比，S2更恰當，因此，將詞語w標注義項S1屬于義項不當。例如，在《詞林》中，“專注”與“注意、留意、經意、在意、小心、留心”同類，但實際上 “專注”與“專心、專心致志、全神貫注”同類要更恰當一些，因此，《詞林》對“專注”的標注就屬于義項不當。

給定詞語w，如果自動標注結果錯誤，而這個錯誤原因是因為詞典對w的一個同義詞或近義詞w1標注錯誤造成的，我們稱之為其他不當。例如，在《詞林》中“跳水”被歸入體育運動類，但是類似的“跳高、跳遠”卻沒有體育運動類的義項。這一類數量較少。

所謂正確指的是： 詞典標注結果正確，自動標注結果錯誤。這一類體現了不同語義詞典在分類標準上的差異性，在一部詞典中歸入同一類的詞語，在另一部詞典中卻屬于不同的類別。比如HowNet中的human類，在《詞林》中則被分為許多類。又如，在HowNet中有CatchUp這一類，“補課、補交”都屬于這一類，但是在《詞林》中“補課”與“聽課、講課”在一類，與“補交”相隔甚遠。

5.2 語義詞典歸類不當現象自動發現

每一條雙向平行類推規則和成對替換類推規則都會有一些正例和一些反例。在這些規則及對應的正例和反例基礎上，我們給出用于發現詞典中可能的缺失義項和不當義項的算法。

基于雙向平行類推規則的算法如下：

給定兩個語義詞典T1和T2，分別為待處理詞典(比如《詞林》)與參照詞典(比如HowNet)

(1) 從T1中根據算法1抽取雙向平行類推規則，分別給出相應的正例和反例；

(2) 逐一處理每一條雙向平行類推規則，設為Rulei，設其正例集合為{PE1，…，PEn}，反例集合為{NE1，…，NEm}；

a) 逐一處理反例集合中的每一個詞語NEj，判斷在T2中NEj與正例集合中的任一詞語是否具有相同的語義類

i. 如果是，則標記為“歸類不當”；

ii. 如果否，則標記為“正確”。

基于成對替換類推規則的算法如下：

給定兩個語義詞典T1和T2，分別為待處理詞典(比如《詞林》)與參照詞典(比如HowNet)

(1) 從T1中根據算法2抽取成對替換類推規則，分別給出相應的正例和反例；

(2) 逐一處理每一條成對替換類推規則，設為Rulei，設其正例集合為{PE11、PE12，…，PEn1、PEn2}，反例集合為{NE11、NE12，…，NEm1、NEm2}

a) 逐一處理反例集合中的每一對詞語NEj1、NEj2，判斷在參照詞典中NEj1、NEj2是否具有相同的語義類

i. 如果是，則標記為“歸類不當”；

ii. 如果否，則標記為“正確”。

6 實驗及其分析

本文的實驗以哈爾濱工業大學《同義詞詞林擴展版》為測試詞典，以董振東先生HowNet為參照詞典，從成對替換類推規則的反例中總共找到1 677對可能存在缺失義項或不當義項的情況。本文分析了其中的100對反例(取按拼音升序排列最前面的100對)，其中屬于義項缺失的10對，屬于義項不當的42對，總計存在義項缺失和義項不當的占52%(如表1所示)。示例詳見表2。其中，“前詞”和“后詞”分別指成對詞語中的前一個詞和后一個詞，“人工判斷錯誤類型”指人工對錯誤進行判斷后所給出的分類結果，“位置”指成對詞語中存在問題的具體詞語。例如“挨打、挨斗”這一對詞語是成對替換類推規則的一個反例，即在測試詞典中兩個詞不同類，但在參照詞典中兩個詞語同類，通過分析發現，這一問題是由于《詞林》中對后詞“挨斗”歸類不當造成的，因此“人工判斷錯誤類型”為“不當”。

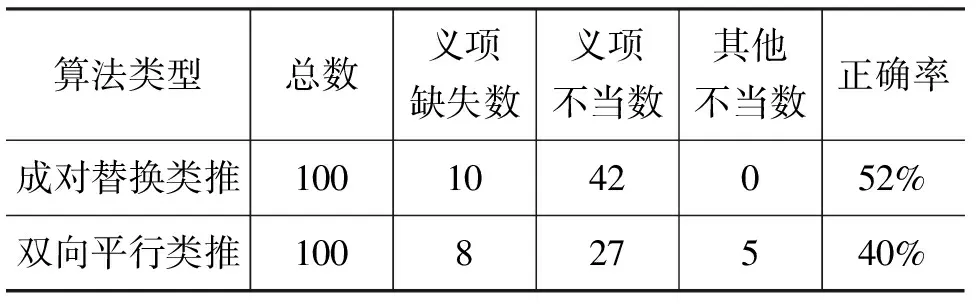
表1 兩種歸類不當現象自動發現算法結果

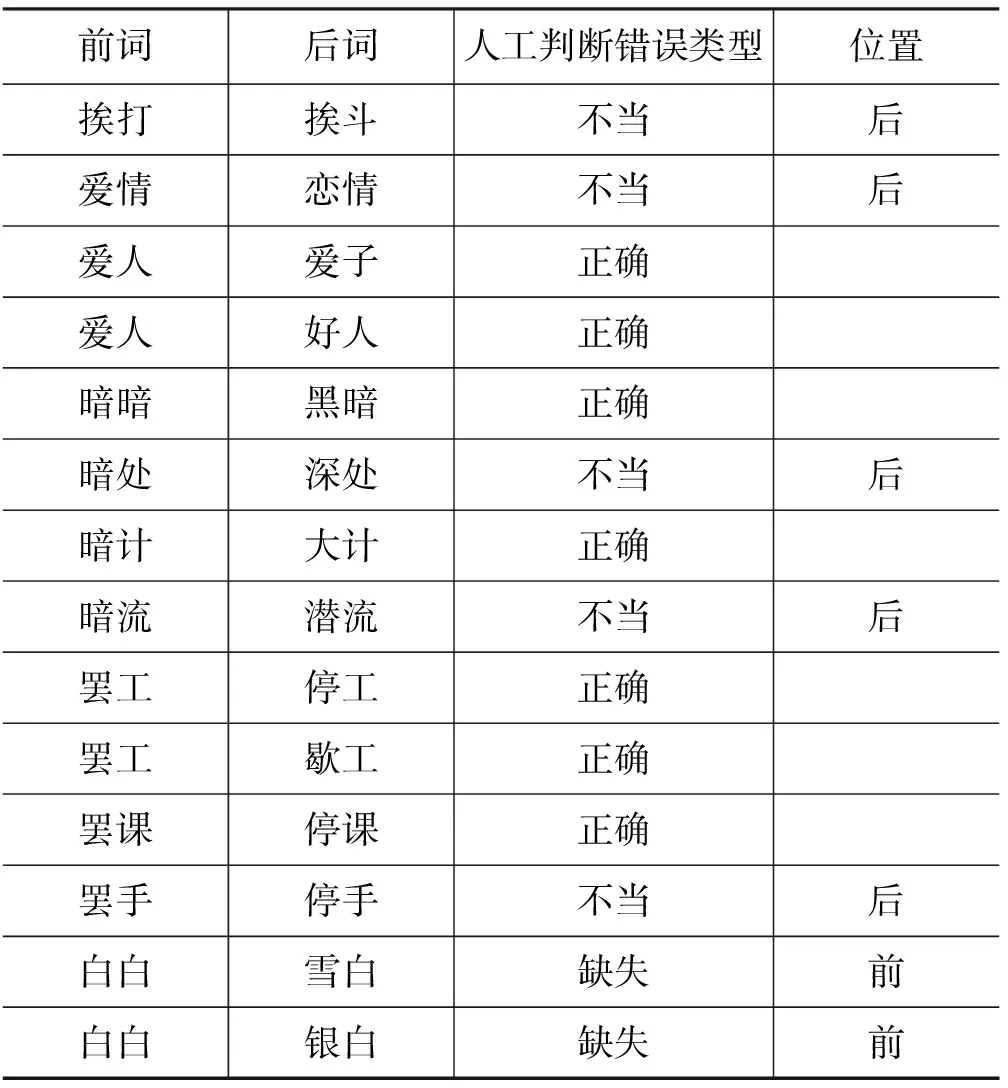
表2 基于成對替換類推規則的歸類不當現象自動發現算法結果分析示例

以《詞林》為測試詞典，HowNet為參照詞典，從雙向平行類推規則的反例中總共找到570個詞語可能存在缺失義項或不當義項的情況。本文分析了其中的100個反例(取按拼音升序排列最前面的100個)，其中屬于義項缺失的8個，屬于義項不當的27個，屬于其他不當的5個，總計存在義項缺失或不當的占40%(如表1所示)。示例詳見表3。其中“反例詞語”指待分析的反例中的詞語，“人工判斷錯誤類型”指人工對錯誤進行判斷后所給出的分類結果，“HowNet中的同類詞語”指依據參照詞典判斷正例中應當與當前反例詞語同類的詞語。例如在《詞林》中“白白”這個詞語是雙向平行類推規則的反例，該規則的正例中包括詞語“白皚皚”；在HowNet中“白白”與“白皚皚”屬于同一類。分析之后發現在《詞林》中“白白”缺少了表示顏色的義項，因此“人工判斷錯誤類型”為“缺失”。

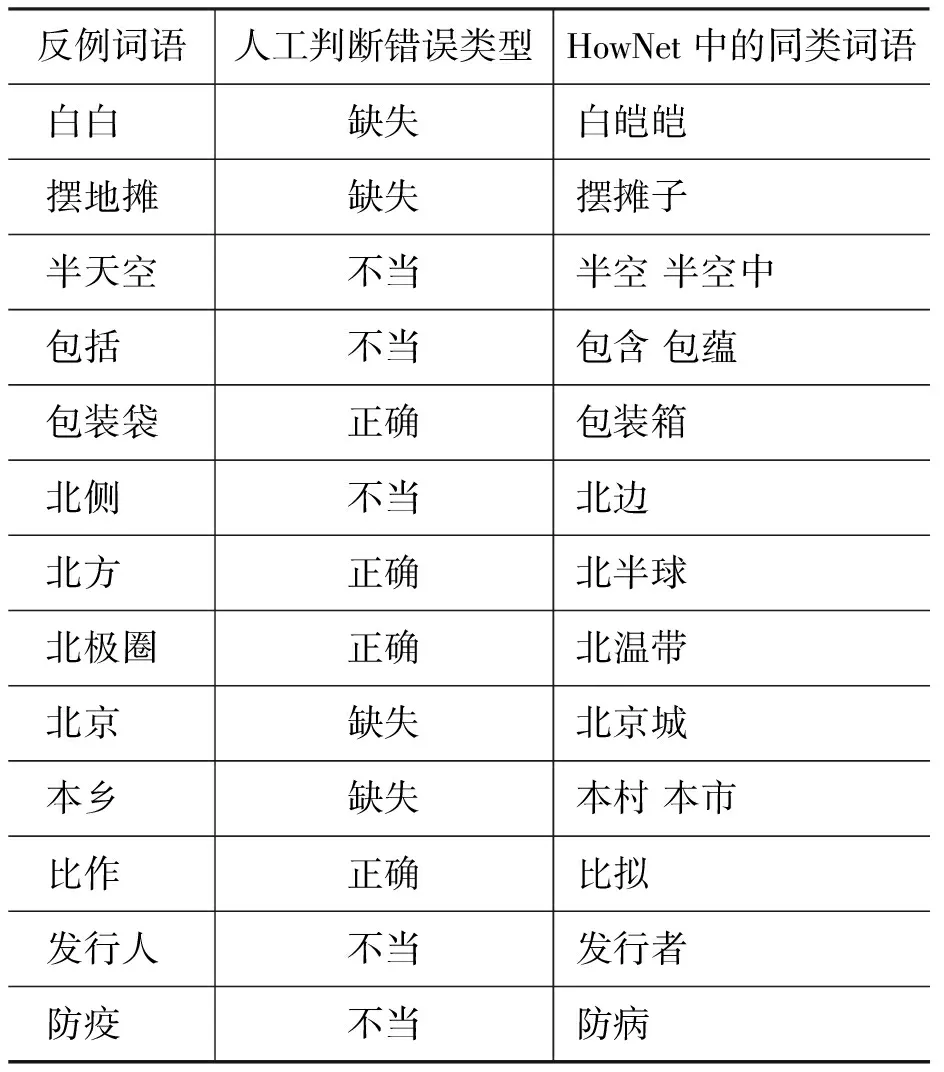
表3 基于雙向平行類推規則的歸類不當現象自動發現算法結果分析示例

7 結論

本文的實驗初步證明了本文提出的方法在語義詞典歸類不當現象自動發現上的有效性。將歸類不當現象自動發現算法同人工校對結合起來，可以將人工檢查的目標從8萬量級降低到千量級，從而可以節省大量人工。

此外，根據目前初步的試驗，基于上下文計算詞語相似度的方法應該也可以應用于歸類不當現象的錯誤發現之中，我們將在另外一篇文章中來討論相關的問題。

致謝

本文在實驗中使用了哈爾濱工業大學信息檢索研究中心的《同義詞詞林擴展版》和董振東先生的HowNet，特此致謝。

[1] 梅家駒，竺一鳴，高蘊琦,等.同義詞詞林[M].上海： 上海辭書出版社, 1983.

[2] D. Dong and Q. Dong. HowNet And the Computation of Meaning [M]. River Edge, NJ, USA: World Scientific Publishing Co., 2006.

[3] 陳保亞.20世紀中國語言學方法論[M].濟南： 山東教育出版社,1999.

[4] 陳保亞.再論平行周遍原則和不規則字組的判定[J].漢語學習, 2005,(1):9-13.

[5] 陳保亞.論平行周遍原則與規則語素組的判定[J].中國語文,2006,(2): 99-108.

[6] 董秀芳.漢語的詞庫與詞法[M].北京： 北京大學出版社,2004.

[7] K. Chen and C. Chen. 2000. Automatic semantic classification for Chinese unknown compound nouns [C]//Proceedings of the 18th International Conference on Computational Linguistics. Morristown, NJ, USA: Association for Computational Linguistics, 2000: 173-179.

[8] H. Tseng. Semantic classification of Chinese unknown words [C]//Proceedings of ACL-2003 Student Research Workshop. Morristown, NJ, USA: Association for Computational Linguistics, 2003: 72-79.

[9] X. Lu. Hybrid Models for Semantic Classification of Chinese Unknown Words [C]//Proceedings of North American Chapter of the Association for Computational Linguistics - Human Language Technologies 2007 Conference. Rochester, NY, USA: Association for Computational Linguistics, 2007: 188-195.

[10] X. Lu. Hybrid Methods for POS Guessing of Chinese Unknown Words [C]//Proceedings of the 43th Annual Meeting of Association for Computational Linguistics Student Research Workshop. Morristown, NJ, USA: Association for Computational Linguistics, 2005: 1-6.