一種改進的BFGS算法及其收斂性分析
陳奎林
(重慶大學數學與統計學院,重慶 401331)
1 問題的提出
本文針對無約束最優化問題:minf(x),x∈Rn開展研究,其中f:Rn→R是一個連續可微的函數。擬牛頓算法中的BFGS算法是一類解決無約束最優化問題的有效算法,這類算法的關鍵是Bk的選取,不同的選取方式,對應不同的BFGS算法。
為了使算法更具優越性,文獻[1-5]在傳統的擬牛頓方程的基礎上提出了一個新的擬牛頓方程,即,其中是一個對稱正定矩陣,從而得到了一類改進的BFGS方法,其迭代公式為
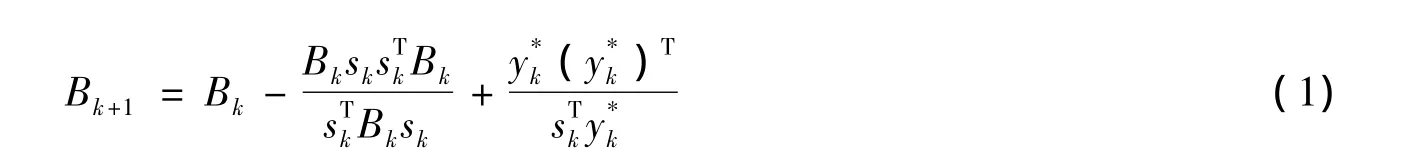
受以上思想的啟發,提出了Ak的一種選取方法,即Ak=‖gk+1-gk‖I,進而提出了一類新的BFGS算法,并證明了它的全局收斂性和超線性收斂性。
本文采用的搜索準則(Wolfe準則)為:

其中0<σ1<σ2<1。
改進的BFGS算法步驟:
步驟1 給出初始點x0∈Rn和初始對稱正定矩陣B0∈Rn×n,令ε>0,k=0。
步驟2 若梯度函數在迭代點xk處滿足‖gk‖≤ε,則停止;否則計算Bkdk+gk=0,求出搜索方向dk。
步驟3 利用Wolfe準則求得步長αk,令xk+1=xk+αkdk。
步驟4 計算Ak=‖gk+1-gk‖I,并代入 式(1),修正Bk得Bk+1。
步驟5 令k:=k+1,轉步驟2。
2 收斂性證明
為證明算法的全局收斂性和超線性收斂性需要以下假設:
①f(x)是二階連續可微的,x*是f(x)的極小點。
②水平集Ω={x|f(x)≤f(x0)}是有界凸集,其中x0是給定的。
③f(x)在凸集Ω上連續可微,且存在一個常數L>0,使得下式成立:
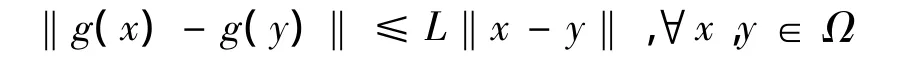
其中:g(x)=▽f(x);‖·‖是Euclidean范數。
④f(x)一致凸,即存在常數m和M,使得
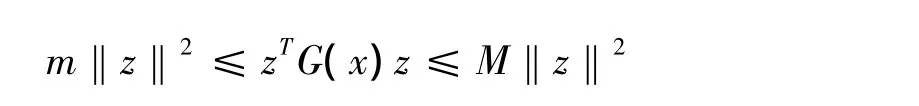
這里?x∈Ω,z∈Rn,其中 G(x)是 f(x)的海色矩陣。
⑤ G(x)在Ω上Lipschitz連續。即存在L'>0使得?x,y∈Ω,有
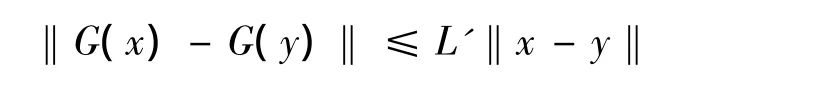
由上面的假設容易得到
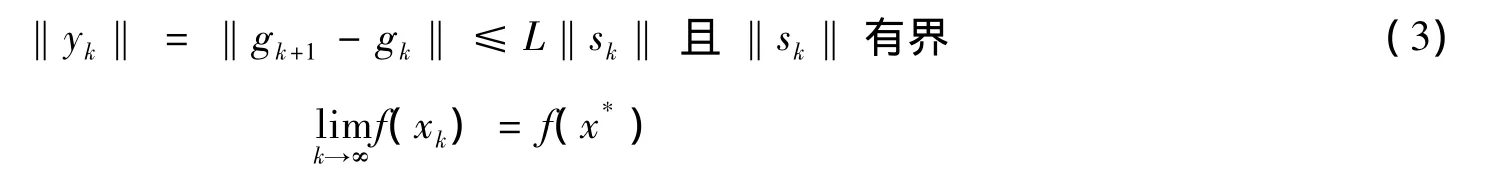
2.1 全局收斂性證明
引理1[4]對任意給定的 k 和由改進的 BFGS 算法產生的(α,x,g,d),若>0,那么
kk+1k+1k+1Bk+1正定。
引理2 若假設(a)、(b)、(d)成立,由改進的BFGS算法產生的點列為 {xk},則,其中sk=xk+1-xk。
證明由Taylor公式,
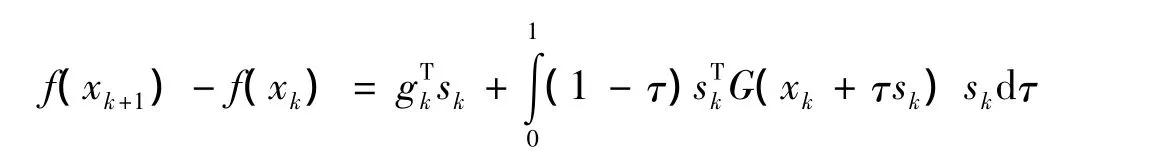
由假設④及式(2)有
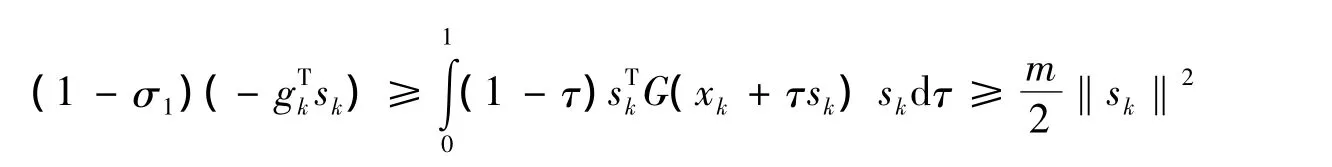
引理3 若假設②~④成立,則式(4)(5)成立

證明
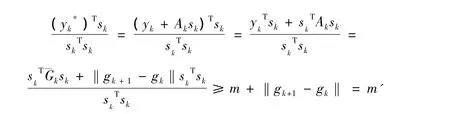
定理1 設x0為任意初始點,f(x)在Ω上滿足假設(a),(d),則對任何對稱正定矩陣B0,由改進的BFGS算法產生的點列 { xk}收斂到f(x)的極小點x*。
證明記,由引理 3 可知 mk≥m',Mk≤M'。
對式(1)有
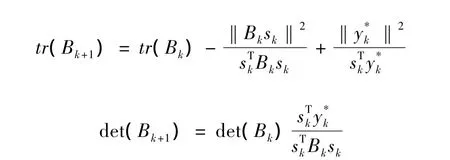
令 ψ(Bk+1)=tr(Bk+1)-ln(det(Bk+1)),則有
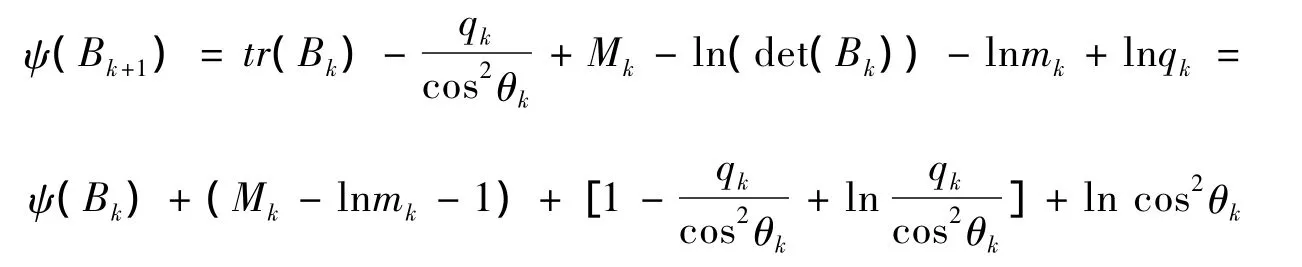
因為函數p(t)=1-t+lnt對任意的t>0都是非正的,所以有
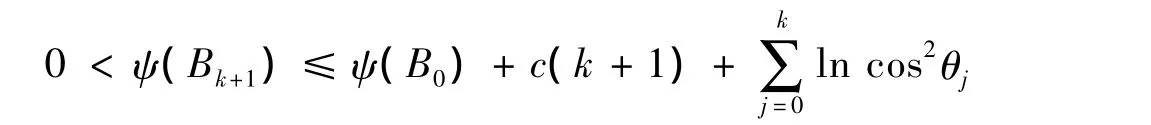
不失一般性,假設 c=M'- lnm'-1 >0,cosθj→0,那么存在 k1>0,使得對?j> k1都有 ln cos2θj< -2c,所以
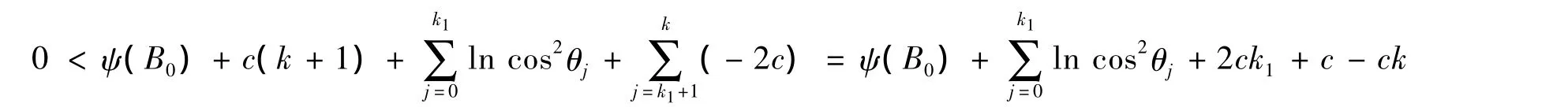
當k充分大時,上式右端的值為負,與左端矛盾,所以假設不成立,從而存在一個子序列 {jk},使得cosθjk≥ε>0。而由文獻[1]中式(3.14)可知lim inf‖▽fk‖→0。又因為目標函數是凸的,所以由改進的BFGS算法產生的點列 { xk}收斂到f(x)的極小點x*。
2.2 超線性收斂性證明
引理4 若{ xk}是由改進的BFGS算法產生的點列,且假設(c)成立,則
證明由 Taylor公式,有 gk+1- gk=G(ξk)sk,其中 ξk=xk+ σsk,σ∈(0,1)。所以 ‖Ak‖=‖gk+1-gk‖≤L‖sk‖,再結合引理2可知成立。
定理2 在假設①~⑤成立的前提下,設以1作為試探步長的Wolfe步長規則下改進的BFGS算法產生的迭代序列 { xk}收斂到最優解x*,且滿足,則 { xk}超線性收斂到x*。證明過程類似于文獻[1]的描述。不再贅述。
[1]王宜舉,修乃華.非線性規劃理論與算法[M].陜西:科學技術出版社,2008.
[2]王安平,馬爍,趙天玉.一種改進的BFGS算法及其全局收斂性分析[J].河北科技大學學報,2009,30(1):8-10.
[3]張恒,何偉.基于新擬牛頓方程的改進BFGS方法[J].淮海工學院學報,2007,16(3):10-12.
[4]WEI Zengxin,LI Guoyin,QI Liqun.New quasi-Newton methods for unconstrained optimization problems[J].Applied Math and Comp,2006,175:1156 -1188.
[5]Jorge Nocedal,Stephen J.Wright.Numerical optimization[M].[S.l.]:Springer,1999.

