有限個漸近非擴張非自映像公共不動點的逼近

戴 敏，向長合

(重慶師范大學數學學院，重慶 400047)

不動點理論是目前正在迅速發展的非線性泛函分析理論的重要組成部分，非擴張映像既是不動點理論中的一個重要內容，又是Banach壓縮映像的一種自然推廣。1972年由Goebel和Kirk引入的漸近非擴張映像是非擴張映像的真推廣。本文在文獻［1］的啟發下引入具誤差的廣義N步非自映像迭代序列，討論了不同條件下有限個漸近非擴張非自映像公共不動點的逼近問題，得到的結果是對文獻［1－6］的推廣。

1 預備知識

定義1［2］設K是Banach空間X的子集，映象F:K→K稱為漸近非擴張映象，如果{k}是實數序列

i且滿足

定義2［3］設E是Banach空間，C是E的非空非擴張收縮核，B:E→C是非擴張保核收縮映像。設T是C到E的非自映像，稱T為漸近非擴張非自映像，如果存在序列，滿足

定義3 2007年，文獻［1］研究了具誤差的廣義N步迭代序列 {xn}，定義為

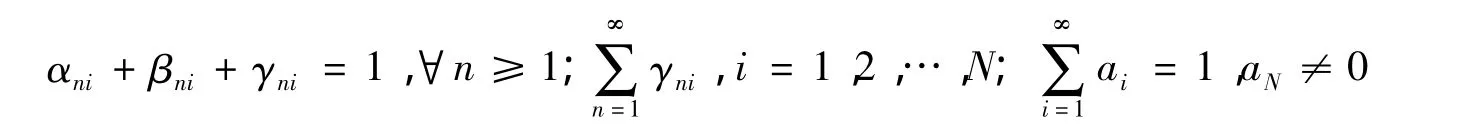
并得到如下定理:

定理1［1］設E是滿足Opial條件的一致凸Banach空間，C是E的非空閉凸子集C是N個具有公共不動點的漸近非擴張映像，其公共漸進系數kn滿足。若式(1)中出現的序列{βni}?[b，c]?(0，1)，i=1，2，…，N，則由式(1)定義的具誤差的廣義N步迭代序列{xn}弱收斂于T，T，…，T的某一公共不動點 x*∈C。

在定理1中，要求T1，T2，…，TN是C→C的自映像，若T1，T2，…，TN變為C→E的非自映像，上述結論是否成立呢?本文將證明對如下定義給出的N步迭代序列，相應結論仍然成立。

定義4 設C是Banach空間E的非空凸子集，T1，T2，…，TN是從C到E的映像，x1是C中給定的一點，則具誤差的廣義N步非自映像迭代序列 { xn}定義為

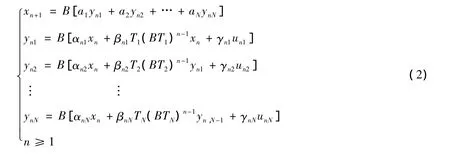
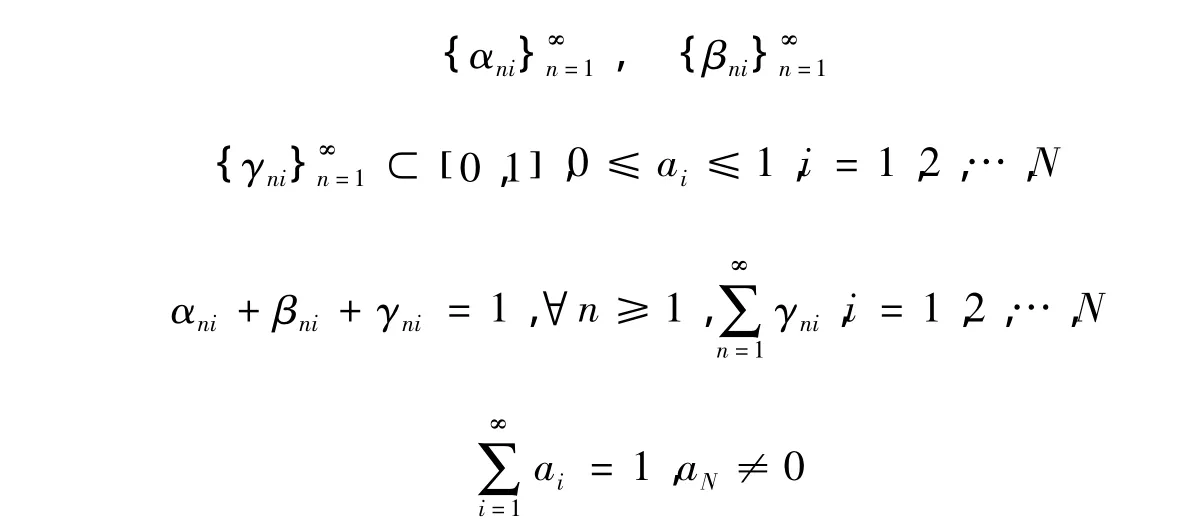
為得到不同條件下具誤差的廣義N步非自映像迭代序列分別弱收斂和強收斂于有限個漸近非擴張非自映像公共不動點，引入如下引理:

引理1［4］設是3個非負數列，滿足cn，n≥n0，其中 n0是某非負整數，則極限存在。

引理2［5］非自映像半閉原理。設E是一致凸Banach空間，K是E的非空有界閉凸子集。設T:K→E是完全連續的漸近非擴張映像，漸進系數 { kn}?［1，∞)，且當n→∞時kn→1，則I－T在0點半閉。

引理3［6］設 E 是一致凸 Banach 空間，若

2 主要結果

引理4 設E是賦范線性空間，C是E的非空子集，T1，T2，…，TN:C→E是N個具有公共不動點的漸進非擴張非自映像，{xn}是C中任意給定的一個點列，若，且，則

證明

定理2 設E是滿足Opial條件的一致凸Banach空間，B:E→C是非擴張保核收縮映像，C是E的非空閉凸子集，又是E的非擴張收縮核。T1，T2，…，TN:C→E是N個具有公共不動點的漸近非擴張映像，其公共漸近系數 kn滿足。若式(2)中出現的序列{βni}?[b，c]?(0，1)，i=1，2，…，N，則由式(2)定義的具誤差的廣義N步非自映像迭代序列 { xn}弱收斂于 T1，T2，…，TN的某一公共不動點x*∈C。

證明因非空，任取p∈F。首先，證明極限存在。由于是C中有界點列(i=1，2，…，N)且極限存在，令

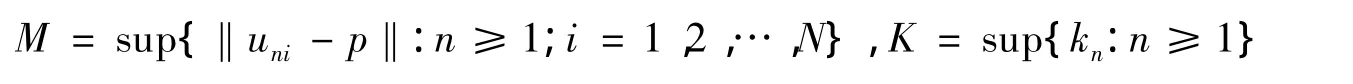
有

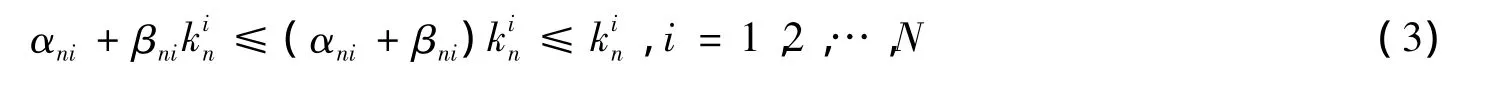
由式(3)和序列(2)得

運用數學歸納法，可得到

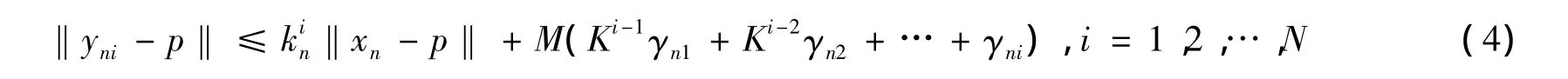
從而，有

然后，證明點列{xn}滿足引理5的條件。由式(4)和式(5)得

于是

又

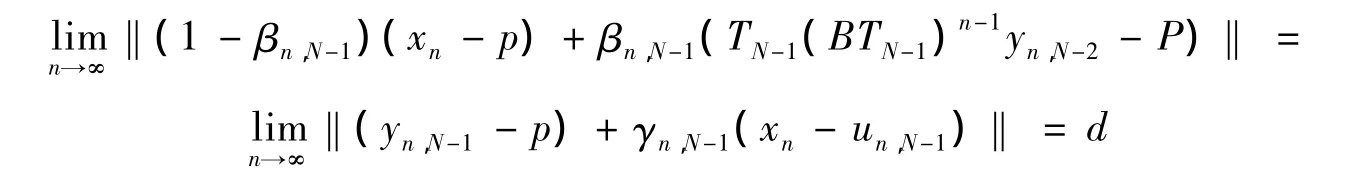
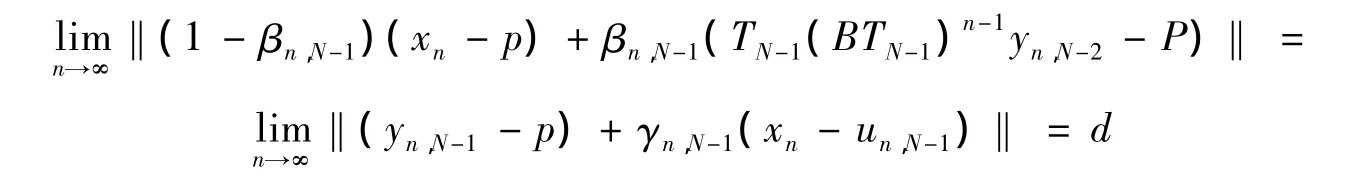
再次由式(5)及式(7)(其中i=N－1)，根據引理3，得

利用數學歸納法，有

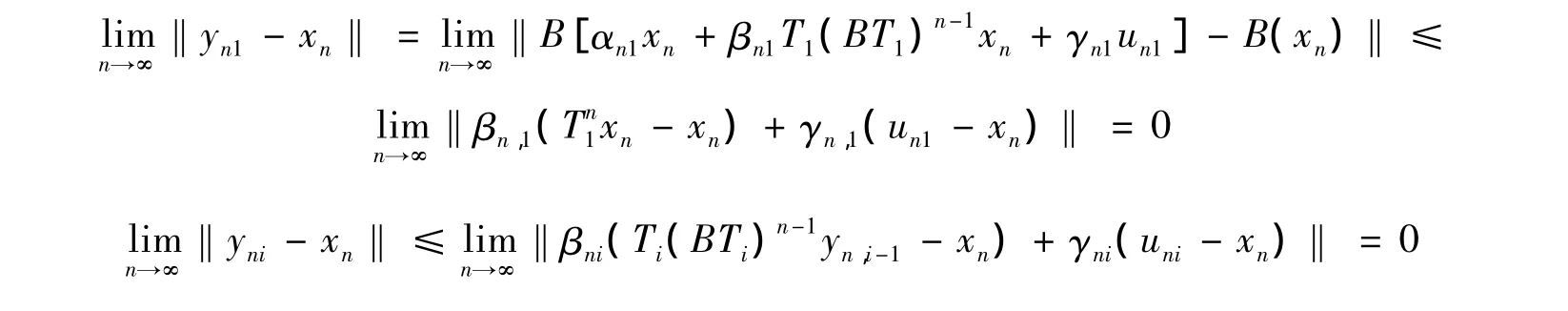
又由

即，點列{xn}滿足引理4的條件。根據引理4，有

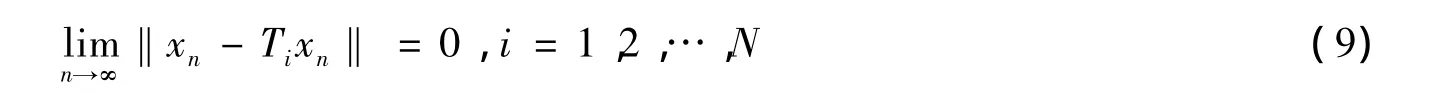
由于E是一致凸Banach空間，因而E是自反的，C中有界點列{xn}必有子列{xnk}弱收斂于E中某個點x*。因為C是E的閉凸子集，所以C弱閉，從而x*∈C。由式(9)N。根據引理2，(I－ T)x*=0，i=1，2，…，N，即，x*∈F。

最后，證明{xn}弱收斂于x*。若不然，由于E自反，存在{xn}的子列{xmk}弱收斂于C中異于x*的點y*，同樣根據引理 2得 y*∈F。又因為任給 p∈F，極限存在，特別地，和都存在。由于E滿足Opial條件，有

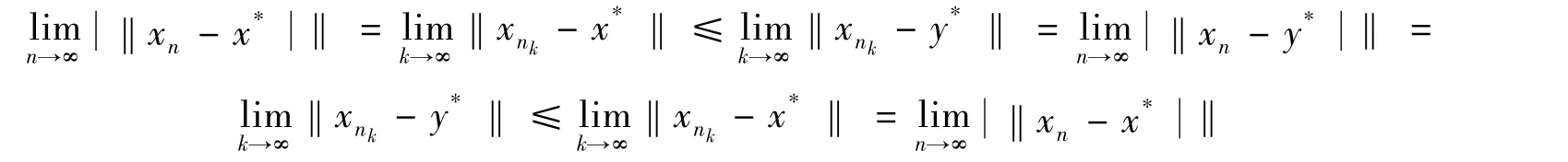
矛盾。因此，{xn}弱收斂于x*∈F。證畢

同文獻［1］可得到如下定理:

定理3 在定理2的條件下，若T1，T2，…，TN中至少有一個是半緊的，則由式(2)定義的具誤差的廣義N步非自映像迭代序列{xn}強收斂于T1，T2，…，TN在C中某一公共不動點x*。

［1］向長合.有限個漸近非擴張映像公共不動點的逼近［J］.重慶師范大學報:自然科學版2007，24(1):7－10.

［2］Goebel K，Kirk W A.A fixed point theorem for asymptotically nonexpansive mappings［J］.Proc Amer Math Soc，1972(35):171－174.

［3］Tian Y X，Chang S S，Huang J L.On the apporximation problem of common fixed points for a finite family of non-self asympotptically quasi-nonexpansive-type mappings in Banach spaces［J］.computers ＆mathematics，2007(53):1847 －1853.

［4］Zhou Y Y，Chang S S.Convergence of implicit iterative process for a finite family of asymptotically nonexpansive mapppings in Banach spaces［J］.Numer Funct Anal and Optimiz，2002，23:911 －921.

［5］Chidume C E，Ofoedu E U，Zegeye H.Strong and weak convergence theorems for asymptotically nonexpansive mappings［J］.Math Anal Appl，2003，280:364 －374.

［6］Schu J.Weak and strong convergence to fixed points of asymptotically nonexpansive mappings［J］.Bull Austral Math Soc，1991，43:153 －159.