二次交通事故Duffing振子模型研究＊

張文會 李 平

（東北林業大學交通學院1） 哈爾濱 150040） （長安大學公路學院2） 西安 710064）

交通事故發生后，如不適合簡易程序處理，就需等待交通警察到達，封閉現場后進行勘查.事故現場的客觀存在導致部分車道封閉，過往車輛要變換駕駛行為，從而導致路段車頭間距等交通流參數變化，車速離散性增大，橫向沖突增加.因此，在一段時間內，事故現場路段的安全性最差.如果駕駛員判斷或操作失誤，過往車輛就會沖入現場，誘發二次交通事故.二次交通事故是初次事故的繼發事件，與初次事故相比，往往導致更加嚴重的人員傷亡和財產損失.公安部和交通運輸部等部門頒布了多項法規，規范了交通警察的安全裝備、勘查行為和現場處置方案，對二次交通事故的發生起到一定的預防作用［1－2］.

查閱文獻，對二次交通事故的致因理論分析較少，只可見基于系統動力學［3］和BP神經網絡模型［4］的分析方法，這是由于我國還沒有針對二次交通事故做相關數據統計，一些對數據依賴性較強的量化模型并不適用.混沌學是研究非線性系統復雜、隨機且不可預測的行為現象，揭示確定性系統的隨機性的一門學科［5］.1963年美國氣象學家Lorenz發現混沌現象，至今混沌理論已有較大發展，并且在很多非線性系統的預測［6－8］和控制［9－11］中有所應用.本文基于混沌理論，分析二次交通事故的混沌特性，建立二次交通事故的Duffing振子模型，并對模型進行仿真分析，以期在缺乏統計數據的條件下，進行二次交通事故的致因分析.

1 Duffing振子模型

1979年P.Halmes基于隨機振動提出了Duffing振子模型［12］，見圖1.將細長的彈性薄鋼片固定于剛性框架，下面放置2塊磁鐵，當框架做簡諧振動時，鋼片的動力學方程即為Duffing振子模型.框架靜止時，鋼片僅受磁力呈平衡狀態；簡諧振動使鋼片受到框架的驅動力和非線性的磁鐵吸引力，鋼片即呈混沌振動.

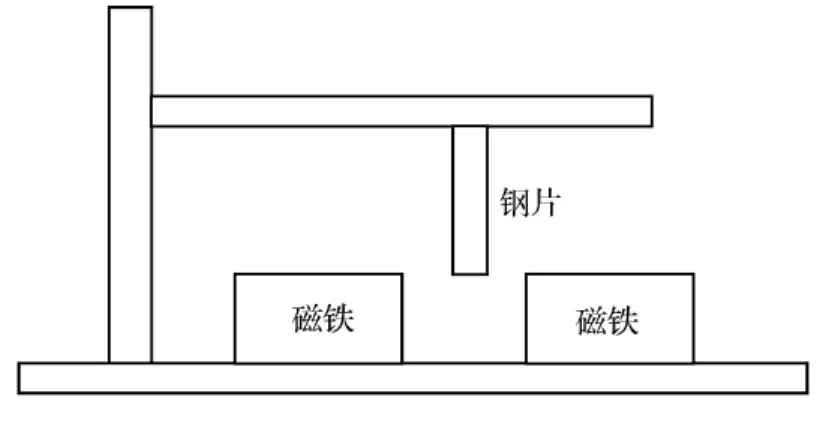
圖1 隨機振動模擬圖

振子的運動方程可描述為

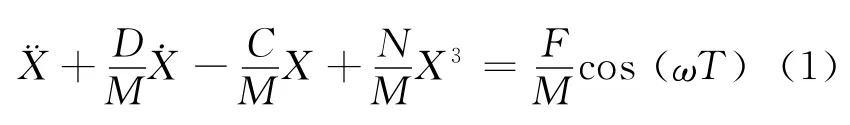
式中：M為質點的質量，kg；D為阻尼系數；C，N為線性及非線性系數；F為外界對振子的作用強度，N.

式（1）描述的是線性與非線性的疊加，參數D／M和N／M分別為線性項和非線性項系數.同時也說明鋼片受到兩塊磁鐵的相互作用，做非線性運動，整個系統也就成為非線性系統；當受到外界作用時，即框架的簡諧振動，系統將發生混沌振動.這種混沌現象表現為有序與無序的統一：當對系統結構進行調整時，即變化式（1）中各個參數值，系統振動將在有序與無序間變化.

引入無量綱參數X＝αx和T＝βt，并做變量代換，得到簡化后的方程為

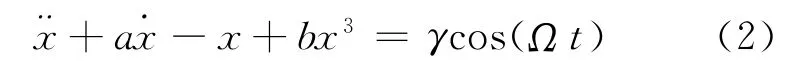
參數a，b的不同取值表示不同的阻尼，改變a，b值，系統將在無序和有序間變化.

2 二次交通事故的混沌特性與建模

2.1 二次交通事故的混沌特性

交通事故發生后，過往事故現場的車輛、圍觀人員、處理事故現場的工作人員和事故路段的交通環境等構成了一個復雜、動態的非線性系統.二次交通事故的發生具有對初始條件的敏感依賴性，如疲勞的駕駛員如果得不到及時休息，就會反應遲緩、判斷失誤或誤操作，易導致車輛沖入事故現場，誘發二次交通事故.以上均是由于初始誤差導致系統誤差變得越來越大，導致二次交通事故的發生.由于駕駛員處于能動地位，通過調整駕駛行為，卻可避免二次事故.因此，二次交通事故的不確定性是混沌現象內在隨機性的表現，其突發性、傳異性是混沌現象對初始條件的敏感依賴性的表現.因此，二次交通事故的演變過程可視為事故現場安全狀態變化過程，而且是一個混沌系統.

二次交通事故的發生與混沌系統具有極大的相似性，具體表現為：

1）均處在非線性系統框架下.混沌現象的發生是在設定的系統框架下得出的，即非線性振動系統.交通事故現場路段的過往車輛、圍觀人員、事故現場處理人員和交通環境等也共同組成了復雜的非線性系統框架.

2）系統的結構在狀態變化過程中起支配作用.混沌方程中的各個參數代表了結構的非線性程度，不同的參數值影響系統向混沌狀態的演變.對于發生事故后的道路交通系統來說，事故路段成為整條道路的瓶頸，安全性最差，人、車、道路環境的協調耦合是事故現場路段安全性的前提，若其中一個因素失調，如車輛超速行駛或路面有積雪等，都會影響交通安全系統結構，駕駛員需不斷改變駕駛狀態，從而使二次交通事故的發生演變為混沌狀態.

3）不同結構的系統產生不同的演化過程，而且通過調整結構組成，可以改變系統的演化方向.當改變混沌方程中的各個參數時，就會得到不同的混沌現象和自組織現象.在發生事故后的交通系統中，通過提前分流，人為減少通過事故現場路段的車輛數量，或者采取更加安全的處置方案，如分段限速或警示標志的合理設置等，調整交通系統的結構，可以提高事故現場路段的安全性.

2.2 二次交通事故混沌模型

根據二次交通事故的混沌特性，建立混沌動力學模型，該模型描述了交通系統在不同條件下的各種狀態及其變化.

式中：Z為初次交通事故現場安全系統的狀態（包括初始事故現場狀態、混沌狀態和二次交通事故發生狀態）；˙Z為系統狀態變化速度；¨Z為系統狀態變化加速度；δ為過往車輛的性能系數；ε為事故路段道路環境系數；σ為事故現場人員系數；t為時間變量；θ為系統參數.

由式（3）知，道路環境對車輛性能以及現場人員特性均有影響，符合人機工程學原理，求解微分方程得

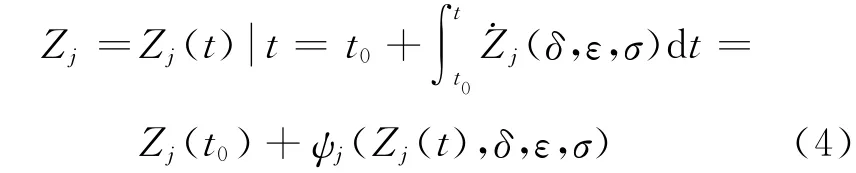
由式（4）知，Zj（t0）為當前的安全狀態，可預知；事故現場的安全狀態預測值為ψj（Zj（t0），δ，ε，σ），是非線性函數，且只和結構參數Zj（t0），δ，ε及σ有關，通過改善以上結構參數值，可提高事故現場路段的安全性，可見，所建混沌動力學模型可以描述二次交通事故的演變過程.

3 二次交通事故混沌模型仿真

3.1 模型仿真

由式（3）的Duffing振子模型，令εδ＝0.3，εσ＝0.2，θ＝1，其根軌跡和相平面圖見圖2和圖3.

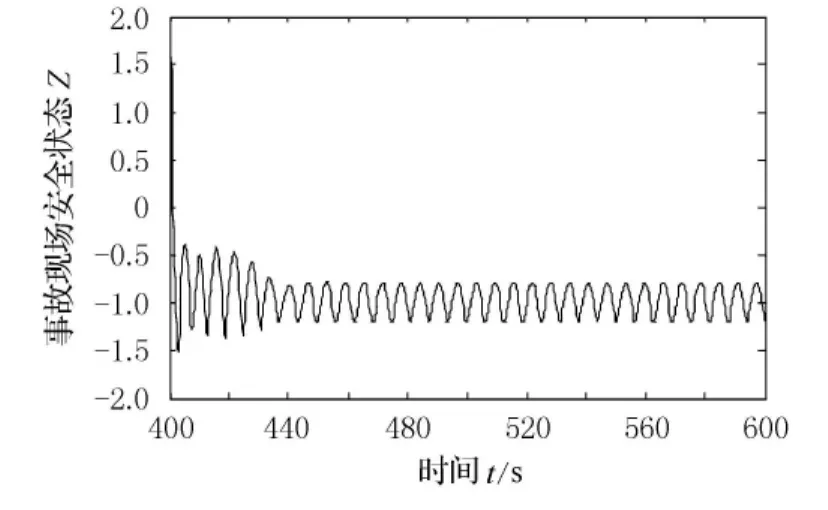
圖2 εδ＝0.3，εσ＝0.2，θ＝1時根軌跡圖

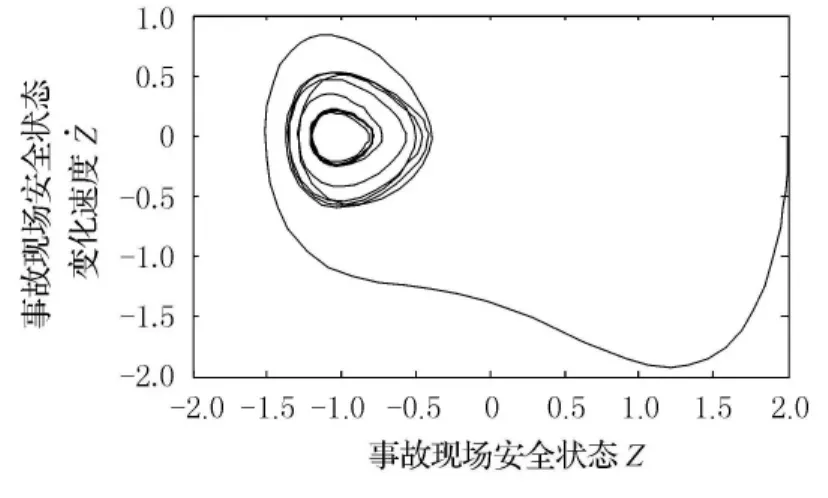
圖3 εδ＝0.3，εσ＝0.2，θ＝1時相平面圖

由圖2和圖3知，事故現場安全系統為周期振蕩狀態.

令εδ＝0.3，εσ＝0.5，θ＝1，其根軌跡和相平面圖見圖4和圖5.

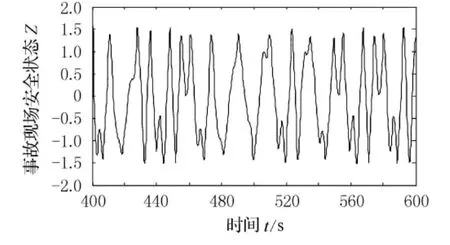
圖4 εδ＝0.3，εσ＝0.5，θ＝1時根軌跡圖

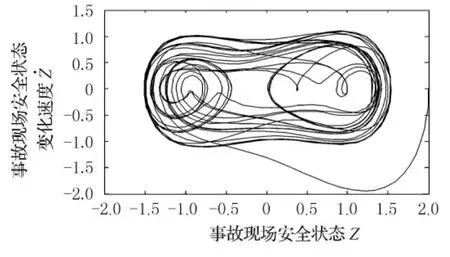
圖5 εδ＝0.3，εσ＝0.5，θ＝1時相平面圖

由圖4和圖5知，事故現場安全系統為混沌狀態.

比較圖2和圖4，在混沌狀態下，事故現場安全狀態的振幅較大，對外界條件的變化較敏感，這也反映了二次交通事故具有極強的可預防性，即改善事故現場的車輛性能技術參數δ、道路環境參數ε或事故現場人員參數σ，就可能避免二次交通事故.

3.2 實例分析

2008年6月哈大（哈爾濱至大慶）高速公路發生一起特大交通事故，根據文獻［4］建立的事故現場安全性指標體系和指標分級標準，經過現場測試和調研，得到各指標實測值和量綱一的量值，見表1.

表1 某交通事故現場安全性指標實測值與無量綱值

將表1中各指標的無量綱值歸一化處理，得到混沌模型中各參數值：σ＝0.250 4；δ＝0.111 4；ε＝0.638 2.仿真得到系統根軌跡圖和相平面圖，見圖6和圖7.

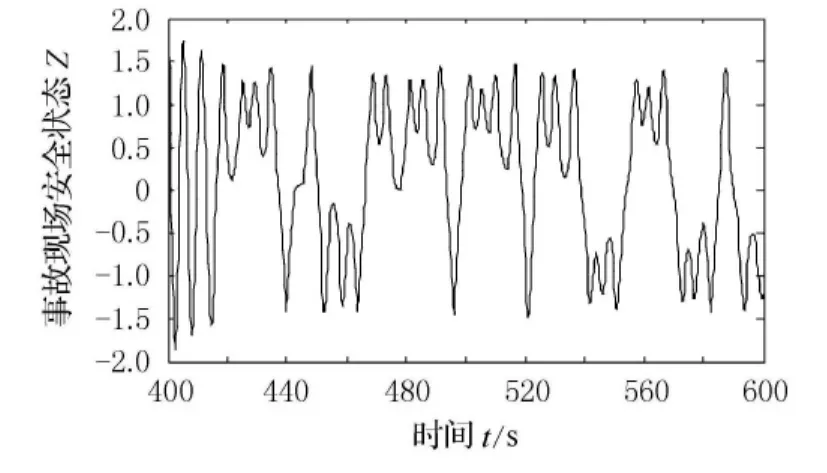
圖6 根軌跡圖

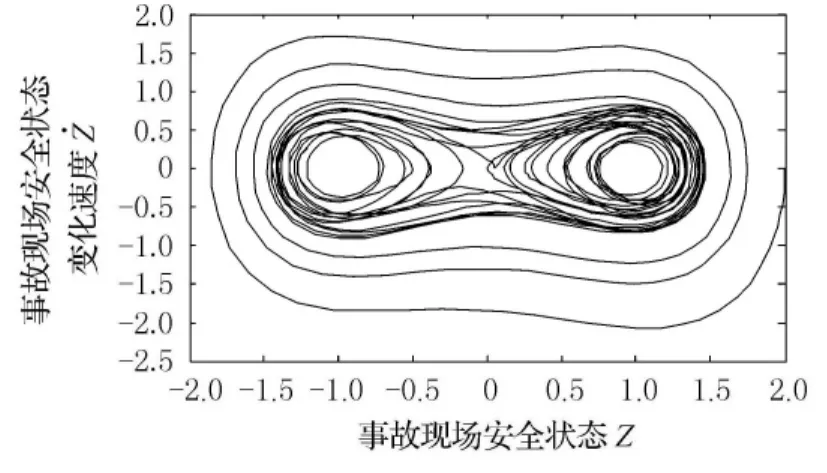
圖7 相平面圖

由圖6知，該交通事故現場安全系統處于混沌狀態，系統狀態變化比較敏感；由圖7可見，相點曲線吸引于焦點（＋1，0）、（－1，0）；當事故現場安全狀態Z確定時，其變化速度Z？時正時負，說明事故現場處于某一安全狀態下，各安全性指標耦合的結果有時加快二次交通事故的發生，有時減緩二次交通事故的發生，事故現場非線性系統的主觀因素在安全性動態變化過程中起到主要作用.例如，提前提醒駕駛員事故現場的存在，提高駕駛員安全意識，控制故障車輛和超載超限車輛數量，改善道路環境條件等，可使事故現場安全狀態變化速度為正方向，即可能避免二次交通事故.

4 結束語

二次交通事故是一類特殊的交通事故，與一般交通事故相比，帶來更嚴重的人員傷亡和財產損失，因此，其致因理論和演變過程分析尤為重要.基于Duffing振子動力系統，建立了二次交通事故混沌模型，分析了二次交通事故的混沌特性；通過仿真，模型中參數值的變化可使安全系統處于周期振蕩狀態和混沌狀態；實例分析結果表明，所建模型可用于二次交通事故的演變過程分析，但對所建模型混沌吸引子以及混沌模型中的參數量值的選取應進一步研究.

［1］中華人民共和國公安部.交通事故處理程序規定［S］.北京：人民交通出版社，2008.

［2］中華人民共和國公安部.交通警察道路執勤執法工作規范［S］.北京：人民交通出版社，2008.

［3］張文會，許洪國.交通事故現場管理安全測度評價［J］.交通信息與安全，2009，27（1）：89－93.

［4］張文會，鄧紅星，王憲彬，等.交通事故現場安全性綜合評價［J］.交通運輸系統工程與信息，2010，10（3）：110－114.

［5］黃潤生，黃 浩.混沌及其應用［M］.武漢：武漢大學出版社，2005.

［6］李 松，劉力軍，賀國光.基于跟馳模型的交通流混沌轉化影響因素的仿真研究［J］.公路交通科技，2007，24（12）：104－108.

［7］張社奇，張廣軍，雷瑞德.沙漠化土地陣子模型研究［J］.中國沙漠，2001，21（1）：1－4.

［8］蔣金泉，李 洪.基于混沌時序預測方法的沖擊地壓預測研究［J］.巖石力學與工程學報，2006，25（5）：889－895.

［9］Her Terng Yau，Jun Juh Yan.Chaos synchronization of different chaotic systems［J］.Applied Mathematics and Computation，2008，197：775－788.

［10］Illing L.Digital communication using chaos and nonlinear dynamics［J］.Nonlinear Analysis，2009，71：2 958－2 964.

［11］Zhang Jiangang，Yu Jianning，Chu Yandong，et at.Bifurcation and chaos of a non－autonomous rotational machine systems［J］.Simulation Modelling Practice and Theory，2008，16：1 588－1 605.

［12］Halmes P.Randomly transitional phenomena in the system governed by Duffingps equation［J］.Journal of Statistic Physics，1979，20：181－196.