變槳軸承空載摩擦力矩的有限元分析計算
汪洪,胡寶成,陳原
(1.洛陽LYC軸承有限公司,河南 洛陽 471039;2.洛陽軸研科技股份有限公司,河南 洛陽 471039)
風力發電機用變槳轉盤軸承安裝在槳葉的根部,用于連接槳葉與輪轂。變槳軸承多為雙排四點接觸球軸承。為了提高承載能力,鋼球與溝道間采用過盈裝配。此類軸承對內、外圈兩排溝道的溝形及溝間距的一致性有很高的要求。內、外圈溝間距不一致時會使摩擦力矩急劇增加,嚴重影響軸承運轉的靈活性。兩排鋼球的裝配過盈量不一致時,會造成偏載,影響軸承的承載能力和使用壽命。實際生產時,為了保證軸承質量,要求在空載時分別測量裝入雙排鋼球和單排鋼球時軸承的摩擦力矩,并將兩者的比值(以下簡稱力矩比TR)作為一個重要的質量控制指標。關于變槳軸承理想力矩比TR的具體值,軸承的供需雙方有時會產生一定的分歧,但都無法提供可靠的理論依據。為此,采用有限元分析技術,結合軸承的實測結果,探索該指標的數值計算方法。
1 力矩比TR
力矩比TR可以綜合反映軸承溝道的加工和裝配質量。其理想值是指軸承空載并且其內、外套圈的兩排溝道尺寸及裝配過盈均達到理想狀態時,裝入雙排球和單排球后摩擦力矩的比值。顯然,當內、外圈溝間距相差較大時,力矩比TR會大大超過其理想值。相反,當雙排球的裝配過盈量相差較大時,力矩比TR會小于理想值并趨近于1。
運用經典軸承理論進行分析計算,得出力矩比TR接近于2的結論。然而,其是以套圈的剛性假設為前提的,認為彈性變形僅發生在鋼球與溝道接觸處的微小范圍。因為假設套圈是剛性的,即使一排鋼球與溝道間存在很大的過盈量也不會對另一排鋼球的接觸產生任何影響。從這個意義上講,力矩比接近于2是合理的。然而,套圈的剛性假設對于變槳軸承是不能成立的。因為變槳軸承套圈的有效壁厚通常遠小于其直徑,受載后容易發生整體彈性變形。因此,對于變槳軸承的計算,只有將整個套圈視為彈性體,其計算結果才會更接近真實情況。為此,采用有限元分析技術進行摩擦力矩的分析計算。
2 有限元分析模型
在進行空載摩擦力矩的測量時,變槳軸承水平放置,僅承受重力。由于在通過鋼球中心的徑向平面和兩個相鄰鋼球徑向平分面上都存在切向對稱性,在進行套圈分析時,只需要取出內、外圈包含半個鋼球的小的扇形段進行研究即可。單排球的有限元分析模型如圖1所示。

圖1 變槳軸承的有限元分析模型
外載荷為作用于每個單元上的體力,即重力。邊界條件:(1)內、外圈沿兩個側面的法向對稱約束;(2)鋼球沿中心截面的法向對稱約束;(3)外圈底平面沿法向的位移約束。
每個鋼球與內、外圈溝道構成4個接觸對,單排球計算模型的應力分布圖如圖2所示。

圖2 變槳軸承空載時的應力分布圖
3 有限元分析和實測結果
3.1 有限元分析
根據文獻[1],裝入單排鋼球后軸承的總摩擦力矩M為
M=DpwZPμ,
(1)
式中:Dpw為球組節圓直徑;Z為鋼球數量;P為半個鋼球與溝道的法向接觸力之和;μ為滾動摩擦系數。
設裝入單排和雙排鋼球時的摩擦力矩分別為M1,M2;裝入單排鋼球時鋼球與內圈上、下側溝道間的法向接觸力分別為Q11,Q12;裝入雙排鋼球時,鋼球與內圈兩排溝道間的法向接觸力分別為Q21,Q22,Q23,Q24。由(1)式得
M1=DpwZ(Q11+Q12)μ,
M2=DpwZ(Q21+Q22+Q23+Q24)μ。
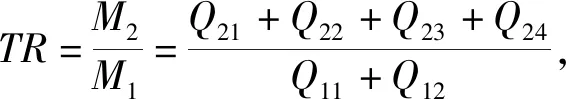
式中的所有法向接觸力按照上述有限元分析方法求出,結果見表1。

表1 有限元分析計算得到的法向接觸力
從表1可以看出,由于內、外圈的彈性變形,雙排球安裝時,鋼球與溝道間的法向接觸力與單排球相比出現了大幅度的下降,使得力矩比TR小于2。計算結果還顯示,隨著過盈量的增加,鋼球與溝道間的接觸力也隨之增大。隨套圈彈性變形的增加,力矩比TR呈減小趨勢,表明鋼球對套圈的擴張作用在不斷增強。此外,對于同一排溝道,其上側溝道比下側溝道承受了更多的載荷。
3.2 實測結果
為了檢測軸承的摩擦力矩指標,選擇了一套加工精度較高,型號為033.38.1900.03的變槳軸承進行了實際測量。為了提高測量的可靠性,使用了不同偏差的鋼球進行對比試驗,試驗結果見表2。從表中可以看出,實測結果與理論計算結果無論是數值上還是變化趨勢上都是十分接近的。
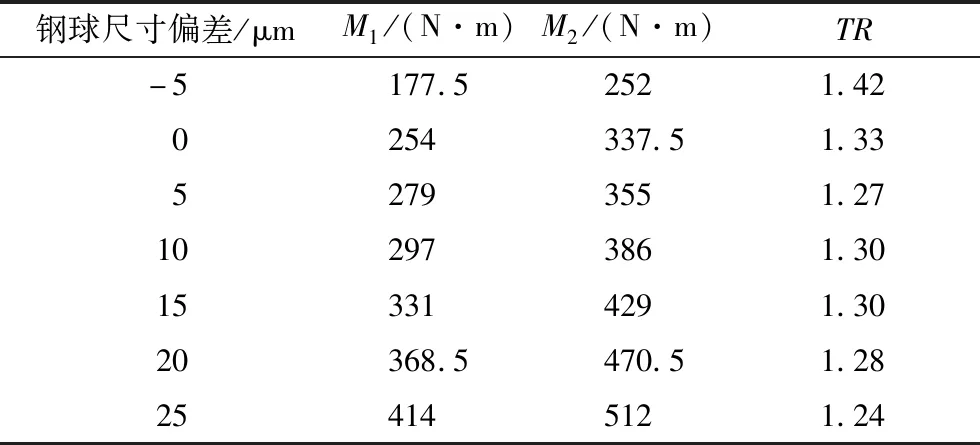
表2 實際測量結果
4 結論
(1) 變槳軸承套圈的彈性變形對于空載摩擦力矩的計算有很大影響,使得同樣大小的鋼球裝配過盈量,安裝雙排球時的法向接觸力小于安裝單排球時的法向接觸力。
(2) 變槳軸承理想的摩擦力矩比TR小于2,大致為1.3~1.4。同時,隨著鋼球裝配過盈量的增大,TR值呈減小趨勢。
理論計算與實測結果的一致性表明,運用有限元分析方法進行變槳軸承啟動摩擦力矩的計算不僅可行且具有較高的準確性。

