航空發動機主軸高速圓柱滾子軸承保持架柔體動力學仿真
楊海生,鄧四二,李晌,陳國定
(1.西北工業大學 機電學院,西安 710072;2.河南科技大學 機電工程學院,河南 洛陽 4710033.洛陽LYC軸承有限公司,河南 洛陽 471039)
航空發動機主軸用高速圓柱滾子軸承使用于高速、高溫、輕載環境下,工作中保持架與多個滾子之間存在著摩擦、磨損和劇烈的碰撞,可能發生運動失穩或疲勞斷裂,引起軸承早期失效,因此保持架的動態性能研究引起了許多學者的關注。文獻[1-2]建立了軸承擬靜力學分析模型并預測了保持架打滑率;文獻[3]建立了動力學模型研究了滾子軸承保持架的不穩定性;文獻[4]研究了套圈為柔性體的滾子軸承保持架的動力學特性,并分析了剛柔耦合產生的影響。文獻[5-6]建立的軸承動力學模型可以計算滾動體載荷分布,動態模擬保持架的打滑。文獻[7]對航空發動機主軸承中保持架的振動特性進行了分析。文獻[8]建立了承受4自由度載荷的滾子軸承動力學模型,分析了工況參數和結構參數對高速滾子軸承動態特性的影響規律。文獻[9]分析了保持架結構參數對軸承動態性能的影響。
從已有文獻來看,大多數圓柱滾子軸承動力學分析模型都是將保持架整體視為剛性體,僅考慮接觸區域的彈性變形;而另一部分文獻雖然將保持架視為柔性體,但對保持架與滾子之間的作用力卻做了簡化假設。航空發動機高速圓柱滾子軸承保持架的梁較薄,保持架整體結構柔性不容忽視;而保持架與滾子之間作用力也與整個軸承工作情況相互耦合。文中將保持架作為柔性體,建立高速圓柱滾子軸承保持架動力學方程,利用ADAMS/SOLVER對方程進行積分求解,對航空發動機主軸高速圓柱滾子軸承保持架動態性能進行仿真。
1 保持架動力學分析模型
在高速圓柱滾子軸承內部各零件相互運動和作用關系基礎上[10],建立了軸承動力學分析模型,模型中考慮了保持架的柔性特性。
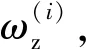

表1 作用力
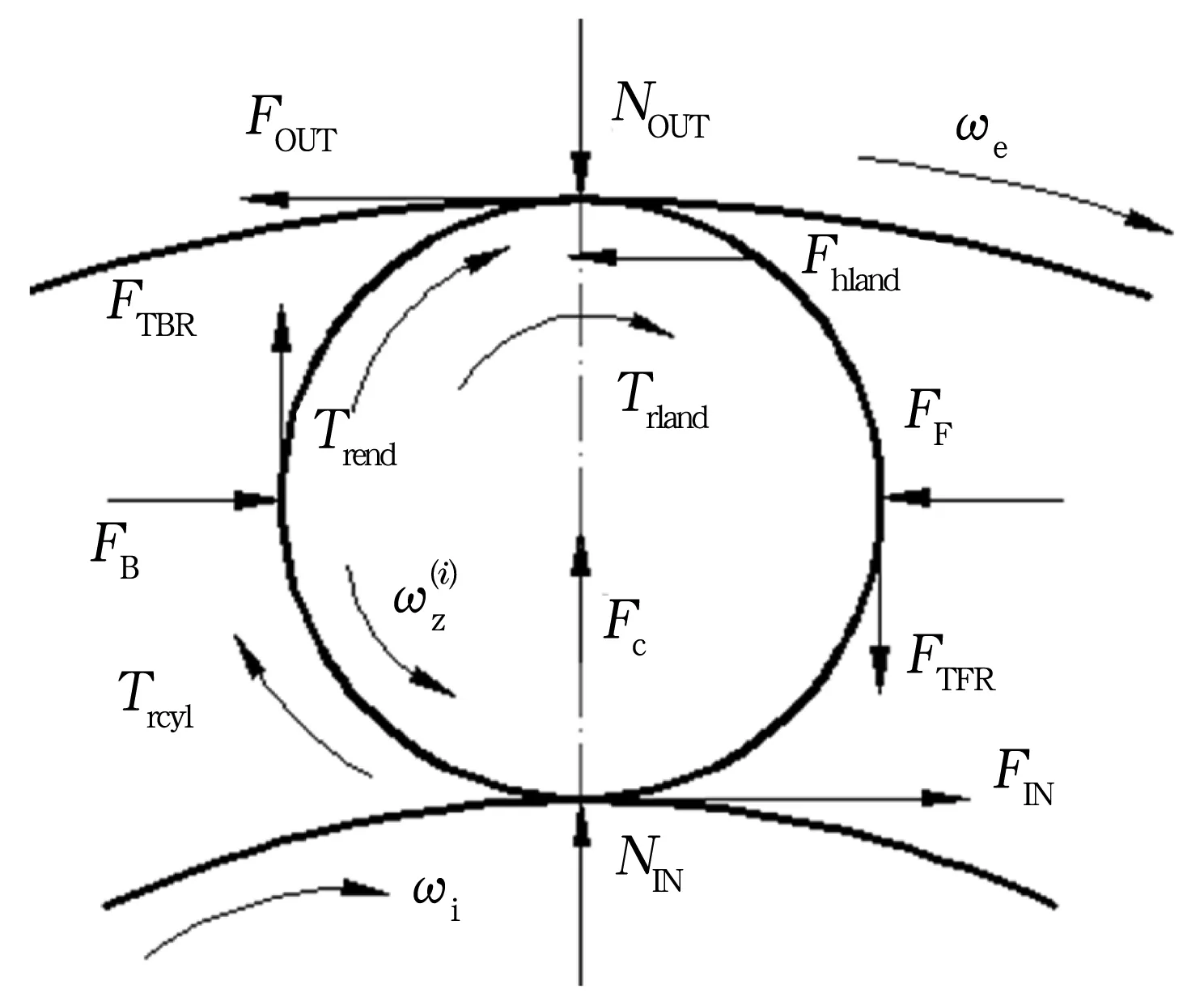
圖1 滾子受力

圖2 保持架受力
根據滾子、保持架和套圈的受力情況,可建立高速圓柱滾子軸承動力學方程。
1.1 保持架運動方程
采用修正的Craig-Bampton子結構模態綜合法[12-13],通過Lagrange方程可得出圓柱滾子軸承保持架的柔體動力學方程
(1)
ζ=[RΩql]T,
Qc=[QtQrQm]T,
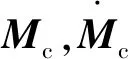
(2)

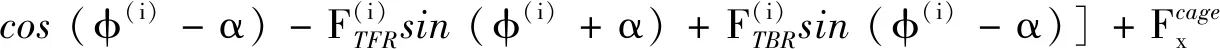
(3)

(4)
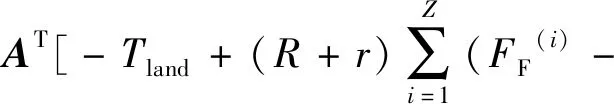
FB(i))-TCDS-TCDO],
(5)
(6)
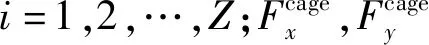
1.2 滾動體運動方程
(7)
Trland(i)-Trend(i)-Trcyl(i),
(8)
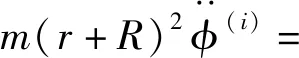
FB(i)-FF(i)+Fhland(i)],
(9)
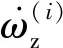
1.3 套圈平衡方程
(10)
(11)
式中:POx,POy為x和y方向上的外載荷;MOx,MOy為外力矩;MF(i),MN(i)為接觸區的摩擦力矩。
2 保持架動力學性能分析
采用Visual Fortran進行ADAMS/SOLVER用戶自定義子程序開發,對每一瞬時圓柱滾子軸承零件位置、姿態、速度及角速度進行實時測量,并據此計算各作用力大小、方向。用戶定義子程序經編譯成為動態鏈接庫(DLL)供ADAMS/SOLVER求解器調用,對 (1)~(11)式組成的圓柱滾子軸承剛柔多體動力學方程組進行求解,從而對圓柱滾子軸承保持架動力學特性進行分析。現針對某型號航空發動機主軸圓柱滾子軸承保持架進行動態性能分析,外圈轉速ωe=12 000 r/min,內圈轉速ωi=10 000 r/min,內、外圈同向轉動,徑向載荷2 000 N,保持架外圈引導,軸承及保持架主要參數見表2。

表2 軸承及保持架主要參數
2.1 保持架模態分析
文中計算了前26階自由振動頻率和模態,據此可以研究其共振、變形狀態。從計算結果來看保持架的振動具有環類零件振動的特性。前6階為剛性模態,系統自動忽略,表3列出了該保持架其余各階固有頻率。從數值上看該保持架的固有頻率最小為538.78 Hz,因此低頻段一般不會發生共振。

表3 保持架的固有頻率 Hz
圖3所示為該保持架幾種典型振型。12階、15階模態分別為保持架在環平面內的彎曲振動,因保持架在環平面內的彎曲剛度較小,振動頻率較低,工作中較易被激發;20階模態為保持架在圓周方向上的彎扭耦合振動;24階模態主要是保持架端面的整體傾斜,發生面外扭轉。從振型分析可以看出,保持架振動時梁易產生較大的剪切應力,最大應力出現在梁的交匯處,因此疲勞裂紋最容易在此處發生,這與實際應用中保持架的失效形式較為一致。

圖3 保持架振型
2.2 工況對保持架動態性能的影響
圖4為不同徑向載荷下保持架的打滑率。由圖4可知:隨著徑向載荷的增加,保持架的打滑率呈減小趨勢,這是由于徑向力的增大會使滾子接觸力增大,從而使滾子與套圈之間的拖動力增大,滾子和保持架的公轉速度也隨之增大,這與文獻[14]中得到的結果相吻合。為避免保持架出現較大的打滑率,應控制最小徑向載荷,文中所研究軸承的徑向載荷為2 000 N時不會出現較大的打滑。
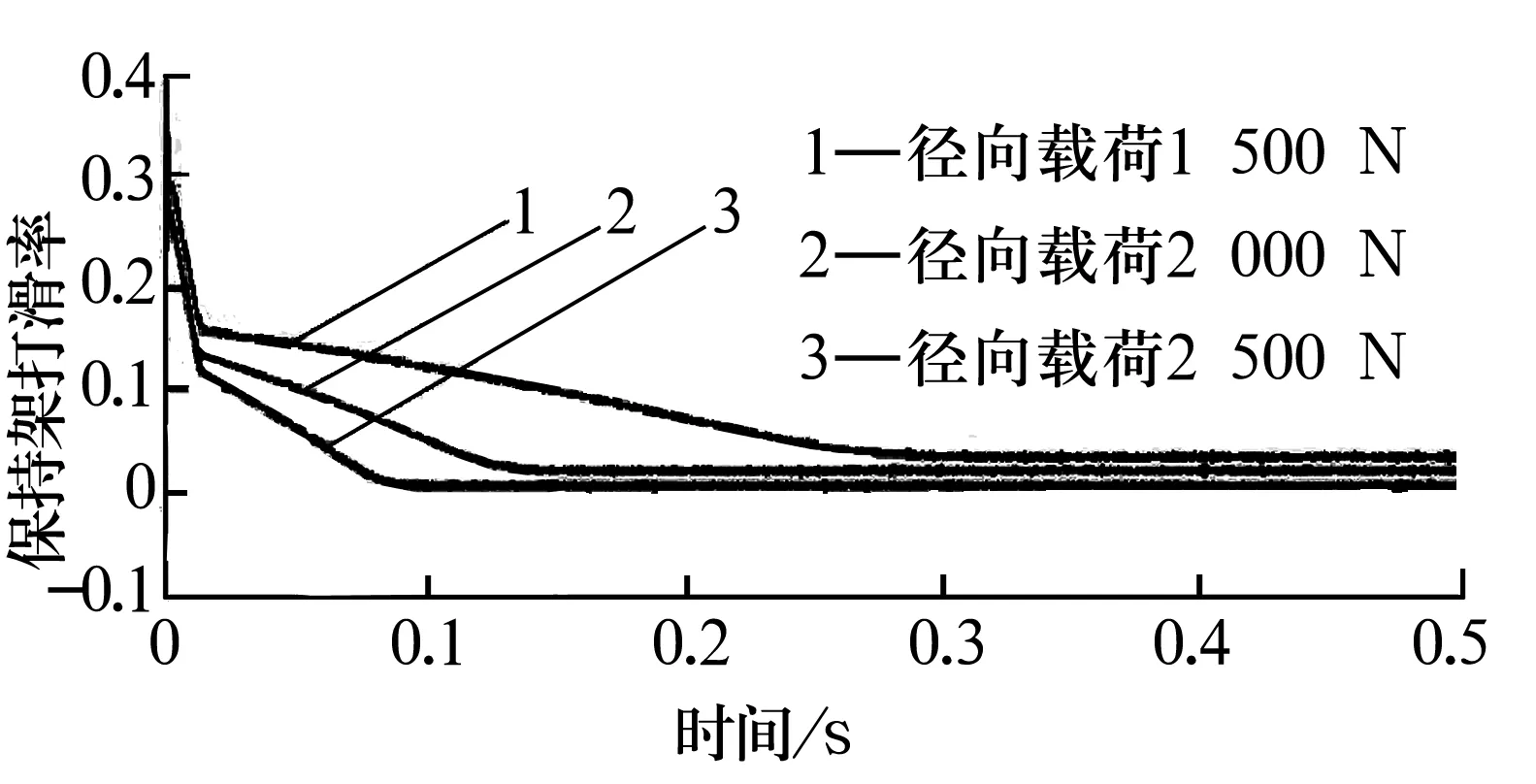
圖4 不同徑向載荷下保持架的打滑率
圖5為軸承外圈轉速不變,內圈轉速對保持架打滑率的影響情況。由圖5可知:隨著內圈轉速的增大,保持架打滑率呈增大趨勢,達到穩態所需時間較長。這是由于內圈轉速提高,滾子與內圈之間拖動力不足,導致保持架公轉速度下降的緣故,這也說明高速輕載軸承打滑是個嚴重的問題。
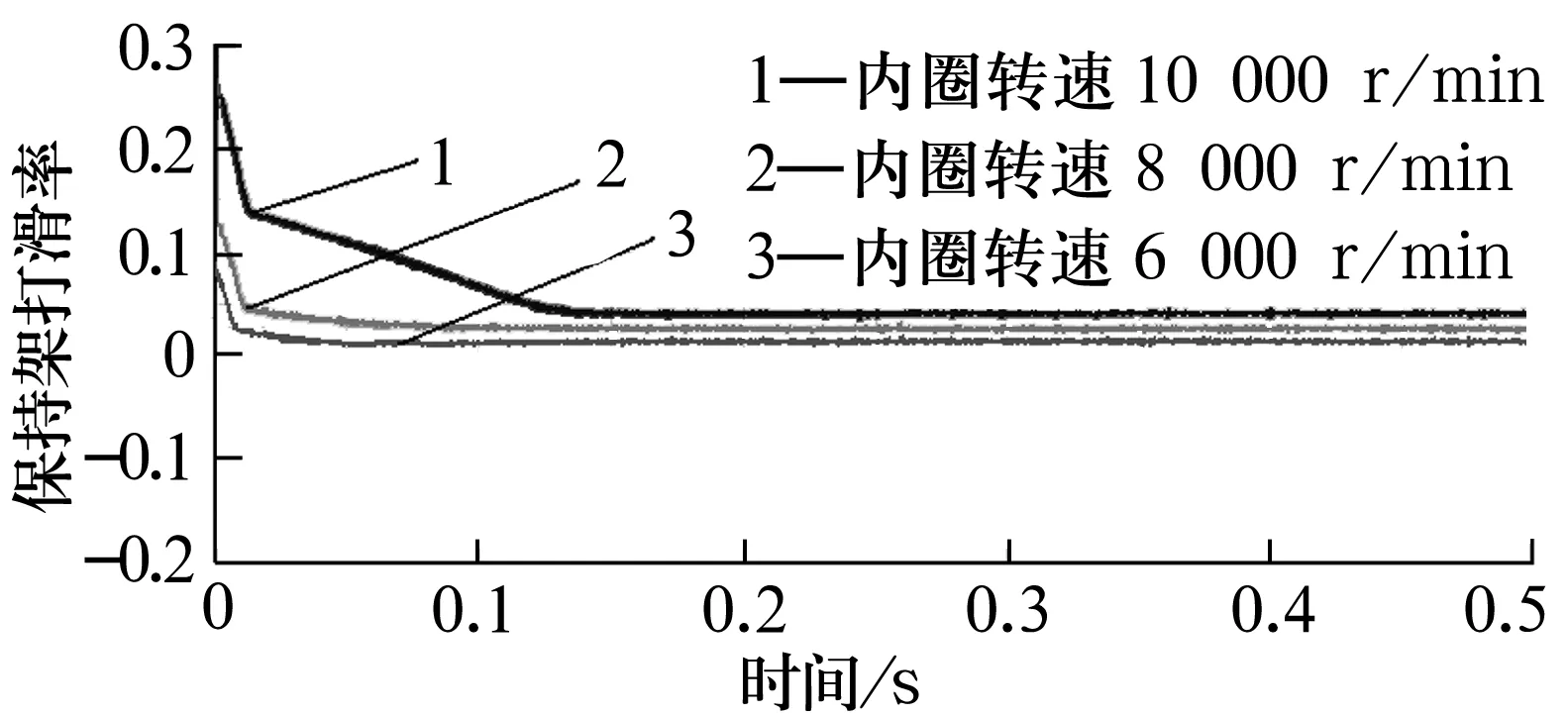
圖5 不同轉速下保持架的打滑率
2.3 結構參數對保持架動態性能的影響
圖6為軸承徑向游隙與保持架打滑率的關系曲線。由圖6可知:在一定范圍內,隨著徑向游隙的增大,保持架的打滑率呈減小趨勢。這是由于徑向游隙的增大,軸承的載荷分布范圍減小,最大受載滾子與滾道之間法向接觸力和切向拖動力增大,最終使保持架轉速升高,因此高速輕載軸承應取較大的徑向游隙值。然而過大的徑向游隙會降低軸承的運動精度,在文中研究的實際工況中,徑向游隙取值較為合理,不會產生較大的打滑。
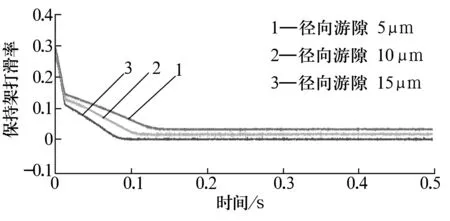
圖6 不同徑向游隙下保持架的打滑率
兜孔間隙與引導間隙對保持架工作特性有較大的影響,文中著重研究了兩間隙的比值的影響情況。表4為不同間隙比下滾子與保持架兜孔之間最大作用力仿真結果。由表4可知,隨著兜孔間隙與引導間隙比值C的增大,滾子與保持架兜孔之間最大作用力也隨之增大,意味著滾子與保持架間的碰撞更加劇烈。仿真結果也顯示出此時保持架運動具有較差的穩定性。工作中,在兼顧其他要求情況下應選擇較小的C值,本文選C=0.5較為合適。

表4 不同C值時滾子與保持架兜孔間最大作用力 N
3 試驗驗證
采用我校航空軸承保持架性能試驗裝置進行試驗驗證。試驗裝置如圖7所示,可進行保持架轉速、位移的瞬態測量。以文中所述某型號航空發動機主軸圓柱滾子軸承為例,進行柔性保持架的打滑率計算,并與剛性保持架和試驗數據進行對比。仿真計算保持架達到穩態后打滑率的均值如圖8所示。與全剛體模型相比,剛柔耦合模型保持架的打滑率更接近試驗值,證明了文中方法的可行性和程序的可靠性。
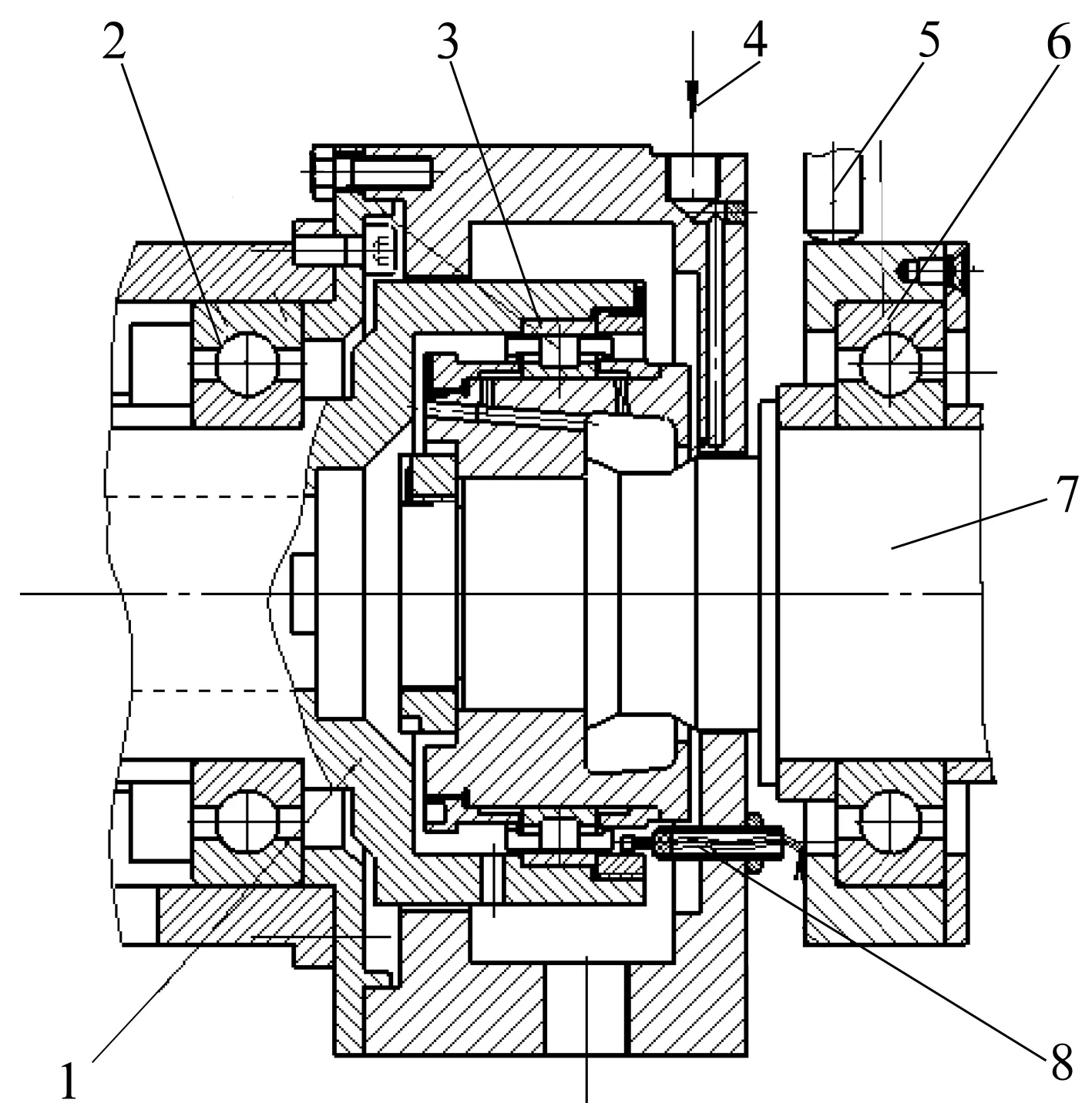
1—外圈軸;2—支點軸承;3—試驗軸承;4—試驗供油;5—徑向加載活塞;6—加載軸承;7—內圈軸;8—測速桿

圖8 徑向載荷與保持架打滑率的關系
4 結論
(1) 保持架振形分析顯示,在梁處易產生較大剪切應力,其最大值出現在梁的交匯處。
(2) 套圈轉速的提高會引起保持架的打滑率增大,為避免保持架出現較大的打滑率,工作中應控制最小徑向載荷。
(3) 徑向游隙的增大能降低保持架的打滑率,但徑向游隙過大同時會影響到軸承運動精度和使用壽命,應根據實際工況選擇合適大小的游隙值,在文中研究算例中,徑向游隙取值滿足要求。
(4) 保持架的穩定性隨著兜孔間隙和引導間隙的比值變大而變差,應在兼顧其他要求情況下選擇較小的間隙比值。

