自主車輛行為決策的安全驗證方法

劉秉政，曹 凱，馬建軍

（1．山東理工大學交通與車輛工程學院，山東淄博255091；2．中國人民解放軍駐上海航天局，上海201109）

混合系統（hybrid system）由連續變量動態系統和離散事件動態系統構成，系統中連續變量和離散事件之間存在相互關聯．也就是說，該系統受不同類型離散事件的觸發，在各自具有不同動態規律的模式間切換．混合系統廣泛存在于商業、工業、交通和軍事領域，特別是對安全性要求極高的系統，如車輛、飛機、導彈、核電站等．在這樣的系統中一個很小的錯誤也會造成嚴重的、甚至災難性的后果．因此，混合系統的安全驗證研究極為重要，且有著重要的科學價值和工程意義，是目前國際上研究熱點之一．

融合了認知科學、智能控制、生理學和心理學、機械電子工程、計算機應用、車輛工程、應用數學等學科前沿科研成果的自主車輛是一個對安全性要求極高的混合系統．對這個混合系統的安全驗證在模擬人類駕駛員操作經驗方面已取得了許多重大成果，但是以系統可達性分析為基礎的自主車輛安全驗證問題卻剛剛起步．目前，國外一些研究者在這一領域已經取得一些的成果：文獻［1] 和［2] 給出了在靜態環境下，車輛對沖突規避的路徑規劃方法；對于動態環境，文獻［3] 提出通過模擬仿真得到不可避免的沖突區域，并對這些區域進行回避，達到安全行駛的目的．

在國內，自主車輛的安全驗證研究主要集中在模擬人類駕駛員操作經驗，并且取得了舉世矚目的成果．在面向車輛主動安全的智能駕駛技術方面，國防科技大學與一汽集團聯合研制的“紅旗旗艦”自主駕駛系統，在高速公路上最高穩定自主行使速度為130km／h，且具備超車功能；吉林大學利用機器視覺系統、三維激光雷達以及GPS實現了緊急制動停車、安全車速轉彎、保持安全車距等功能；清華大學研制的THASV－V，采用計算機視覺和雷達作為傳感器，能夠實現智能巡航、碰撞報警、車道線跟蹤等功能；西安交通大學對車輛主動安全中的障礙物檢測和分類、駕駛員實時姿態和道路的識別等車輛自主和輔助駕駛關鍵技術進行研究；上海交通大學聯合法國國家信息與自動化研究所、葡萄牙Coimbra大學啟動了CyberC3項目，重點研究面向城市環境的無人駕駛車輛，旨在為未來的城市提供一種靈活、高效、安全、環保的新型公交工具［4]．

模擬的最大優點是它能產生一個反例（系統過程軌跡與某一不安全狀態相沖突），以此展現一個系統的不安全狀態．但是，在沒有反例產生的條件下，模擬卻無法證明系統是安全的．為此，本文以系統可達性分析為基礎，實現對自主車輛所有可能路徑的覆蓋，研究其行為決策的在線安全驗證問題．為了滿足在線安全形式驗證對時效性的要求，本文對系統狀態空間以及輸入空間進行離散化，將自主車輛和其他車輛的系統動態抽象為馬爾科夫鏈，實現對車輛狀態隨機可達集快速計算的目的．

1 系統的形式驗證

自主車輛是一個混合系統，它以主動安全為核心，模擬有經驗的人類駕駛員的決策能力和行為特征，通過各種傳感器感知交通環境，理解和預測交通環境的變化以及目標的意圖，規劃安全行駛路徑，確保車輛安全可靠行駛．由于自主車輛的換道、超車、轉彎等邏輯決策行為的動態變化，呈現受事件驅動的離散系統特性，適宜采用離散方法建模；然而在自主車輛的具體決策行為上，車輛的動態特征卻又呈現隨時間發展而不斷變化的連續系統特征，其最佳表達方式則是連續微分方程．因此，在各種不同類型交通事件的觸發下，自主車輛在連續和離散模式間動態切換，表現出更加復雜的混合系統的動態行為．然而，目前對于這種混合系統的動態行為安全性驗證基本采用兩種方法：一是基于人類操作經驗或過程的模擬建模技術；二是以系統可達性分析為基礎的形式驗證技術．由于模擬建模技術從系統的某一初始狀態出發，檢驗系統的一次行為軌跡或操作過程，縱使進行多次模擬仍然可能錯過重要的非安全因素；而形式驗證技術是在系統模擬的基礎上，從系統的某一初始行為狀態集合出發，通過計算系統行為可達集，一次性檢驗所有可能行為軌跡或操作過程，因此可以一次性驗證系統的安全性．

安全驗證的過程就是自主車輛追蹤某一規劃路徑，同時考慮到各種可能的擾動，以此確定一個行為變化范圍（縱向和橫向），即可達范圍，就這個可達范圍推斷自主車輛運行狀態的變化趨勢，并預測未來某一時間間隔內自主車輛的交通行為的安全性．因此，需要計算自主車輛從某一初始運動狀態在未來時間段上的隨機可達集，以及其它車輛在相同時間段上的隨機可達集．判斷自主車輛可達集在未來某一時刻與其它車輛可達集的交集狀態，如果交集是空集，那么自主車輛在規劃路徑上的行駛是安全的，否則為不安全，并計算與其它車輛的沖突概率．系統安全驗證過程如圖1所示．

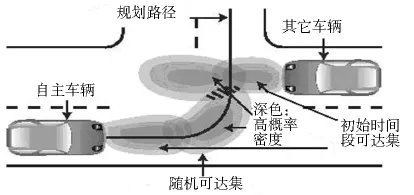
圖1 系統安全驗證過程

2 驗證過程及基本假設

系統安全驗證以自主車輛對環境的感知為依據，因此，給定自主車輛的初始位置、速度以及行駛方向等參數，并依據車輛動態目標位置［5]預先確定自主車輛行駛路徑．自主車輛通過傳感器獲取某一時刻其它車輛的位置、速度等參數，進而對其它車輛的未來行為做出估計．此外，自主車輛可達集的變化范圍與趨勢以其規劃路徑為約束，而其它車輛可達集的變化范圍與趨勢則以自主車輛對其未來交通行為的估計為參考．這種約束和參考的意義在于：整個驗證過程以自主車輛的視角來觀察道路交通環境，而且可達集變化范圍與趨勢力圖反映車輛的真實行為，避免可達集變化無約束擴展，造成無意義的系統安全驗證結果．

對于自主車輛的安全評估而言，預測其它車輛的行為是至關重要的．像人類駕駛員一樣，通常自主車輛預判其它車輛行為的前提條件是：

（1）其它車輛必須遵循道路交通法規，以此排除諸如反向車道中的車輛隨意闖入自主車輛行駛車道等擾亂交通秩序的違法行為．

（2）其它車輛的行為分兩個階段建模，即路徑生成和路徑追蹤．路徑生成可以由諸如車道保持、左／右轉向及車道變換等基本行為軌跡構成，圖2展示的是車輛接近交叉口即將采取的基本行為軌跡．路徑由長度為s，且由滿足條件s≤s′≤2s的Bezier線段組成．對于s′約束條件的理由是確保計算的合理性，使到達交叉口的車輛有盡可能大的行為選擇空間．

圖2 交叉口車輛基本行為軌跡

（3）車輛路徑追蹤的基本行為由靜止、加速、減速和限速行駛等行為構成．

3 模型的建立

3．1 動態目標位置

動態目標位置是自主車輛在跟蹤、轉彎、超車或避讓行駛過程中，依據時間、障礙物位置、距離和方向的變化以及道路線形變化的預判而改變的預期到達位置［5]．它是一個由動態位置坐標和方向組成的向量，即，T＝［xt，yt，θt] ，其中xt和yt為動態目標位置在t時刻的坐標，θt為動態目標位置的車頭方向與水平方向的夾角．在本文的研究中，動態目標位置是自主車輛規劃路徑的終端參照點，它表達了自主車輛根據當前局部交通態勢確定下一步將要到達安全位置的決策過程，這一決策過程是依據停車視距分段進行的．于是，本文依據動態目標位置對自主車輛參考路徑進行建模．

3．2 自主車輛參考路徑

參考路徑表達的是自主車輛當前和未來若干時間段內的狀態變化，由自主車輛當前狀態點、動態目標位置點構成．參考路徑依據自主車輛動態目標位置按長度s進行劃分，并在交叉路口處滿足條件：s≤s′≤2s．依據車輛行駛軌跡的特點，車輛行駛軌跡曲線y＝f（x）應該是連續的，且曲線應具備以下特征：

（1）軌跡曲線分段構成，以便適應道路曲率變化．

（2）軌跡曲線整體是C2連續的．

（3）在軌跡曲線的起點和終點處應當滿足條件．

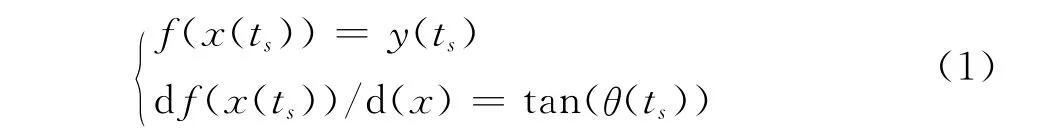
和

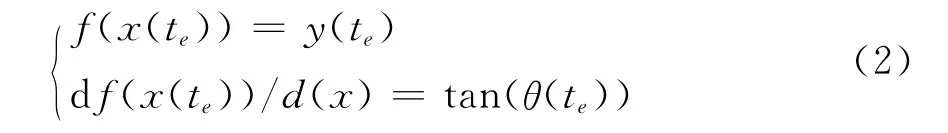
其中，x（ts）和x（te）為曲線段起點和終點．

這里選用貝塞爾（Bezier）曲線進行參考路徑曲線擬合．由于利用Bezier曲線方程進行軌跡生成時，最主要是利用其切矢量性，即Bezier曲線的起點和終點處的切線方向和特征多邊形的第一條邊及最后一條邊的走向一致，因此生成的軌跡具備車輛行駛軌跡曲線特征．

假設已知自主車輛的初始狀態點Ps（x1，y1）和初始速度Vs（朝向角為θ1），自主車輛動態目標點Pe（x4，y4）和速度Ve（朝向角為θ2），則連接Ps和Pe兩點的三階貝塞爾曲線方程為［6]其中，λ為正系數，u的取值范圍為［0，1] ．

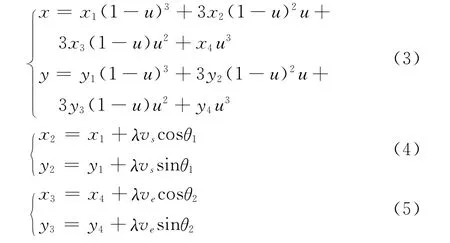
將式（3）～式（5）代入式（1）和式（2），易證采用該方法進行路徑規劃，滿足式（1）和式（2）的端點條件，即該路徑是滿足非完整約束的．

3．3 自主車輛模型

由于車輛在機動行駛中車輪與地面之間有不可避免的滾動約束，使得車輛系統成為最典型的非完整控制系統，而鏈式系統模型可以將非完整系統的難點以簡單的形式表達出來，便于在線處理．

這里，自主車輛模型使用一個前輪轉向四輪運動模型，即

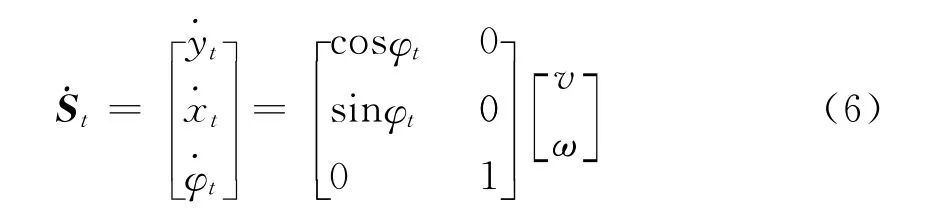
其中，xt，yt為動態目標位置在t時刻的坐標；φt為動態目標位置的車頭方向與水平方向的夾角；v和ω為智能車輛的線速度和角速度．此研究中v是常量，ω則根據上文參考軌跡規劃的不同階段幾何表達式而定．這個模型是一類典型的非完整系統，本文采用文獻［6] 中將車輛運動模型轉化成鏈式系統模型的方法，根據文獻［6] 的推導，設計車輛運動系統（6）的控制如下：

式中，d1，d2為常數，它們對系統有擾動作用，以便當系統初始位置處在奇異點時，能夠使其離開奇異點．

3．4 其它車輛模型

本文以自主車輛的視角為觀察依據進行在線安全驗證，自主車輛通過傳感元件感知周圍環境中的其它車輛．按照前面的基本假設，其它車輛的路徑生成限定為車道保持，因此，對其它車輛車道保持的縱向動態行為采用混合自動機建立一個切換系統模型．混合自動機是描述混合系統的計算模型，它是有限狀態自動機的推廣，可用來描述和計算具有連續和離散變量的混合系統的行為．建立的切換系統模型由靜止、速度限制、制動和加速四個模塊以及它們之間的切換關系構成，如圖3所示．

模型中I為不變集合，E為切換關系（事件），常數c2表示車輛的速度限制，且模型中的切換關系是單向的，即一次切換發生以后，系統的連續狀態隨之發生而無法重現．切換系統模型中的制動模型h1（u）與加速模型h2（v，u）的表達式如下：

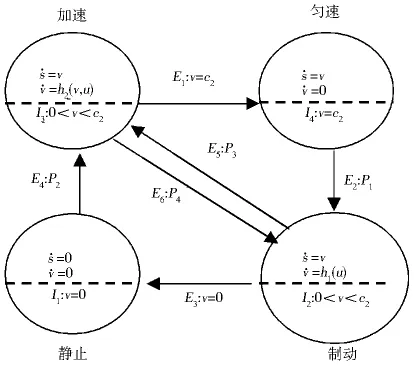
圖3 其它車輛混合自動機模型

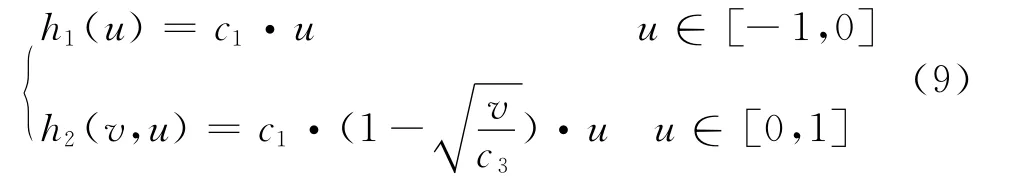
式中，常數c1表示最大加速度，常數c3表示車輛速度上限（這一特定指標因車輛類型不同而不同）．需要注意的是，加速模型和減速模型中的輸入變量u在其邊界內是不確定的，并且切換系統模型的離散動態也包含不確定性．此外，除了切換事件E1和E3以外，其它切換事件E2、E4、E5和E6均以概率Pi（i＝1，2，3，4）隨機發生．

4 系統狀態空間的近似表達

以上基于混合系統構筑了自主車輛和其它車輛模型，下面對模型狀態空間在某一初始條件下的連續變化范圍進行系統可達性建模．為此，需要建立和計算系統狀態可達集．

給定一個車輛的動態表達式：

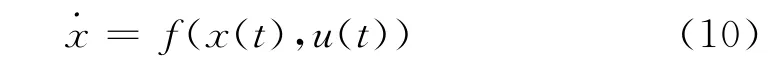
這里的x∈Rn表示狀態，u∈U表示符合萊布尼茲連續條件的輸入．當t＝r時，車輛狀態精確可達集Re（t）表示如下：

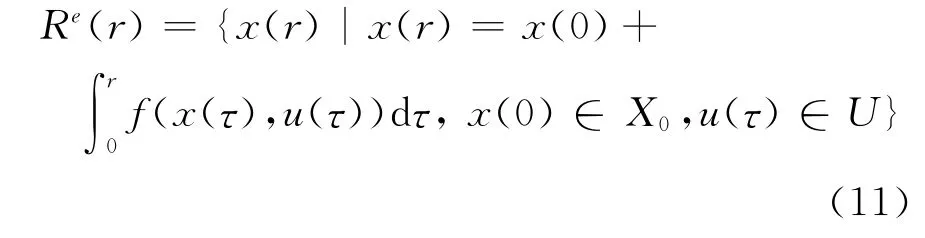
由于計算系統精確可達集僅適用于特殊案例［7]，因此一般采用超近似計算方法求出Re（r）的近似值R（r），使R（r）?Re（r）．因此，某一時間間隔上的超近似可達集可以定義為

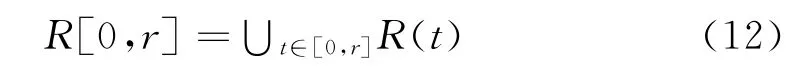
于是，如果假設S（0）＝和V（0）＝分別表示車輛初始位移區間和速度區間，則車輛的初始狀態可以表示為一種聯合狀態形式：

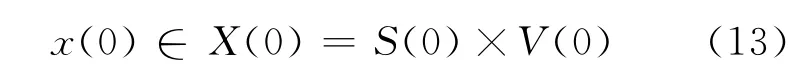
那么，車輛的初始狀態可達集R（t）就可以用位移與速度二維區間近似表示為X（t）＝的計算方法為

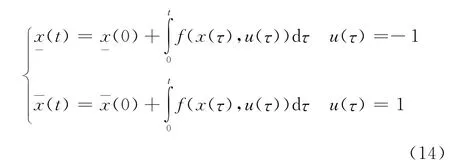
一個馬爾科夫鏈就是由離散狀態z∈N＋組成的隨機動態系統，它包含離散時間的馬爾科夫鏈和連續時間的馬爾科夫鏈．本文采用離散時間的馬爾科夫鏈，于是，時間t∈｛t1，t2，…，tf｝，其中，tf表示預測時間范圍，tk＋1－tk＝T∈R＋為時間步長．馬爾科夫鏈的當前時刻ti狀態無法精確表達，而是通過概率pi＝p（ti）描述．那么，設p為概率分布向量，下一時刻ti＋1概率分布向量p可以表達為前一時刻ti概率分布向量的線性組合，即

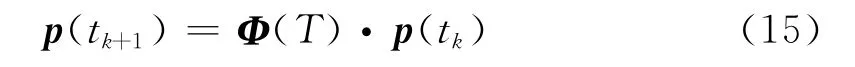
其中，Φ（T）是馬爾科夫過程的轉移矩陣．這里，馬爾科夫模型的建立分為兩個步驟：（1）將初始連續系統的狀態空間分割為若干柵格，以此對系統狀態空間離散化．具體地說，按照車輛的等間隔位移s（與路徑劃分一致）和速度v間隔構成的矩形柵格，由位移s和速度v構成一個二維離散狀態空間．（2）計算由一列柵格轉移到另一列柵格的概率，并將結果儲存到馬爾科夫轉移矩陣中．具體過程如下：

（1）狀態空間和輸入空間的劃分：將連續狀態空間X?R2分割為若干均等矩形柵格Xi，下標i表示相應的離散狀態，每個柵格上的系統狀態坐標（x1，x2）定義為（s，v）．于是，依據式（13）的定義，柵格Xi可以用二維區間Xi＝近似表示，即系統的狀態空間可以近似表示為：X＝∪Xi．類似地，將車輛動態表達式（10）的輸入空間U?R分割為若干區間Uα，即U＝∪Uα，其中上標α表示相應離散輸入值．

（2）馬爾科夫鏈的轉移概率：馬爾科夫鏈的轉移矩陣中儲存的是該系統從狀態i到狀態j的轉移概率Φji（如圖4所示），其中Φji（T）＝p（z（tk＋1）＝j｜z（tk）＝i），而且這一轉移概率也取決于離散輸入值α．因此．對于每一個離散輸入α需要計算一個不同的轉移概率矩陣Φα．為了計算轉移概率（T），假設（T）表示在輸入u∈Uα的影響下，由初始狀態x（0）∈Xi出發，在時間T處的可達集．因此，可以通過計算可達集（T）得到轉移概率的值．為此，本文利用MATLAB的混合系統驗證工具箱Checkmate作為運算平臺，計算可達集（T），從而求得轉移概率．需要注意的是，可達集（T）［8]中的時間T與馬爾科夫鏈的時間步長增量T是相等的，而且由柵格i出發，經過時間T后，到達柵格j的轉移概率（T）等于該時刻可達集與柵格j交集，∩Xj），所占的幾何容積比為

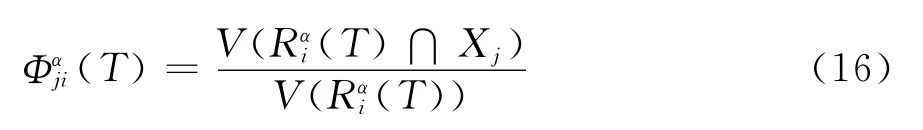
其中V（）表示容積算子．

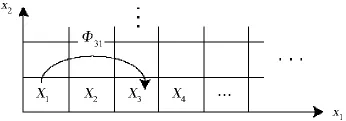
圖4 狀態空間的分割及轉移

由式（16）可以看出，只有當可達集到達某一柵格時，到達這個柵格的概率才是非零的．這就意味著轉移概率矩陣只會儲存當前到達柵格的概率，并替代了此前到達這個柵格的信息．因此，具有非零概率的馬爾科夫鏈可達柵格能夠超近似表達對應的可達集與超近似可達集相比，在式（16）中假設的可達集范圍內這些概率本身是以系統狀態均勻分布的形式近似表達的，即馬爾科夫鏈可用于表達某時刻對應可達集上的系統狀態（如圖5所示）．

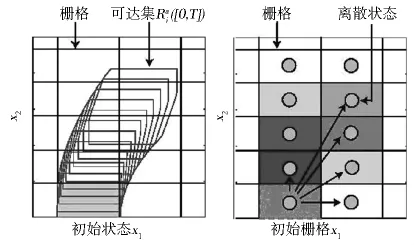
圖5 馬爾科夫鏈對可達集的近似

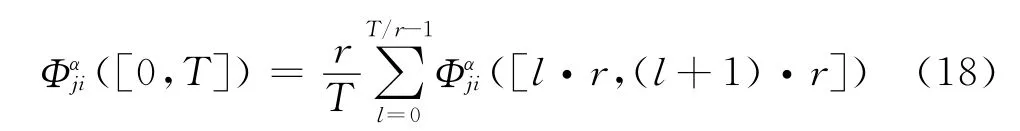
5 在線驗證

系統狀態空間離散劃分之后，隨機可達集完全可以由馬爾科夫鏈的概率向量p表達．由于公式（15）只能針對馬爾科夫鏈進行單次推演計算，而本研究需要根據不同的離散輸入α、時間點以及時間間隔條件建立馬爾科夫鏈，因此，必須擴展公式（15），即對于一個給定的輸入α，依據某一個時間點處分布狀況計算某一時間間隔內的概率分布．于是，時間點處的概率分布可以作為時間間隔計算的支持，即

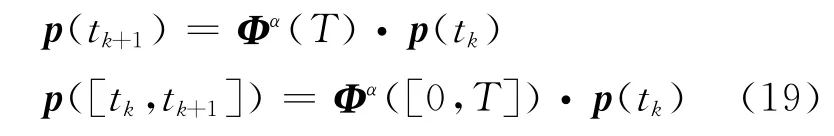
計算自主車輛與其它車輛在規定時間內的馬爾科夫鏈，檢驗兩者的可達集是否相交，若相交，計算得出相交概率，即沖突概率．為了更好地驗證上述提出的方法，本文給出一個如圖6所示的典型交通情形．圖6中，自主車輛保持勻速行駛，其既定行駛路線前方有一個固定障礙物，而且反向車道也有車輛駛來，自主車輛在判斷反向車道車輛位置和速度的基礎上，規劃躲避障礙物軌跡，并依據式（19）進行馬爾科夫鏈推演計算．為此，給出參數設定如下：

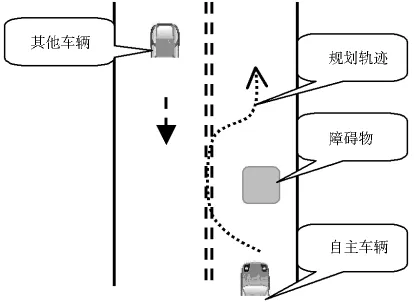
圖6 假設交通場景

自主車輛參數設定：自主車輛均勻行駛速度v＝15m／s，起始位置x0＝［1．8，2．2] m，y0＝［3，6] m，φt＝0＝［－0．01，0．01] rad．

未知車輛參數設定：起始速度v∈［3，8] m／s，起始位置s∈［75，80] m，最大加速度c1＝15m2／s，速度限制c2＝15m／s，速度上限c3＝60m／s．加速輸入u∈［0．2，0．4] ，減速輸入u∈［－0．4，－0．2] ；由圖3可知，未知車輛的行為狀態含有4個模塊，根據起始速度的設定，未知車輛可進入的狀態只包含在加速模塊和減速模塊中，考慮到未知車輛行為信息的不確定性，此處假設加速模塊與減速模塊的發生概率分別為p加＝0．5和p減＝0．5；事件切換概率分別為p1＝p2＝p3＝p4＝0．5．根據以上初始條件，對所有車輛在時間間隔［0，3．2] s上的隨機可達集做出分析預測，并進行安全驗證．

驗證結果如圖7所示，線條表示采用貝塞爾曲線對自主車輛蔽障給出的參考路徑擬合曲線，自主車輛與其它車輛在給定時間范圍內的道路占有概率分布由陰影方塊表示，其中顏色深處表示車輛中心和車體中心的概率分布．在預測時間間隔［0，3．2] s內，當t∈［2．4，3．2] s時自主車輛與其它車輛的沖突概率為0．01，其他時間段內的沖突概率為0，從而驗證了自主車輛蔽障行為安全．

6 結束語

本文將交通參與者的行為建立為混合系統模型，并通過分析系統在初始條件下的可達狀態即可達集來進行在線安全驗證，并且考慮到交通參與者的行為中存在的諸多隨機因素，提出利用馬爾科夫鏈對交通參與者行為的隨機過程進行表示，這種表示方法的應用不僅將隨機因素考慮在內，而且可以大大地縮短在線驗證的時間．

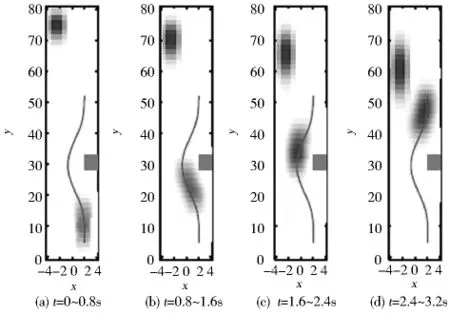
圖7 車輛蔽障安全驗證示意圖

例證表明了此研究提出的方法對于沖突概率的計算具有良好的時效性．如果遇到更加復雜的情況，適當地擴大起始狀態的劃分單元，便可實現簡便與快速的計算，這就使得此方法可以廣泛地運用于諸多交通環境下的安全驗證．

［1] Iwan U，Johann B．VFH＊：Local obstacle avoidance with lookahead verification［C] ／／Proceedings of the IEEE Int．Conf．Robotics Automation，2000：2 505－2 511．

［2] Adrian B，Simon B，Takeo K．A prediction and planning framework for road safety analysis，obstacle avoidance and driver information［C] ／／Proceedings of the 11th World Congress on Intelligent Transportation Systems，2004：270－277．

［3] St′ephane P，Thierry F．Safe motion planning in dynamic environments［C] ／／Proceeding of the IEEE－RSJ Int．Conf．on Intelligent Robots and Systems，2005：3 512－3 518．

［4] 徐昕，賀漢根，蔡自興，等．車輛智能駕駛技術的研究前沿與展望［C] ／／中國自動化大會暨兩化融合高峰會議．杭州：2009．

［5] 曹凱，于少偉，周蘆蘆．基于動態目標位置的智能車輛控制研究［J] ．信息與控制，2008，37（4）：476－480．

［6] 曹凱，周蘆蘆．車輛彎道機動駕駛控制算法［J] ．信息與控制，2011，40（2）：262－267．

［7] Gerardo L，George J．P，Sergio Y．A new class of decidable hybrid systems［C] ／／Proceedings of the 10th International Conference on Hybrid Systems：Computation and Control，1999：137－151．

［8] 劉秉政，曹凱．基于混合自動機的車輛控制建模及可達集分析［J] ．山東理工大學學報：自然科學版，2010，24（增）：72－75．

［9] Matthias A，Olaf S，Martin B．Reachability analysis of nonlinear systems with uncertain parameters using conservative linearization［C] ／／Proceedings of the 47th IEEE Conference on Decision and Control，2008：4 042－4 048．