一類T－S模糊雙線性系統的魯棒控制

馬進峰，俞純權

（山東協和學院經濟管理學院，山東濟南250107）

近年來，雙線性系統及其研究被廣泛地應用于許多領域，如生物工程、生化工程、社會經濟學等方面．雙線性系統是一類比較特殊的非線性系統，介于線性系統和非線性系統之間，其數學模型的非線性部分通常為系統的狀態和輸入的雙線性函數．一般而言，雙線性系統模型比一般的非線性系統結構簡單、動態特性簡單，同時描述對象的近似程度往往比線性系統要高的多［4]．

非線性是工業控制中普遍存在的的現象，對于非線性系統的研究是控制理論中一個十分重要的課題．基于T－S模型的模糊控制是研究非線性系統比較成功的方法之一，應用T－S模型對非線性系統進行穩定性分析和控制器設計方面，已有很多成果面世．同時，由于不確定的存在，魯棒性問題也成為帶有不確定模糊系統所研究的熱點問題．但是目前很多T－S模糊模型中，模糊規則的后件部分多是一個線性函數．文［1] 研究了一類模糊雙線性系統的魯棒穩定性問題，其模糊規則的后件部分是一個雙線性模型，但是在其給出的系統穩定LMI條件中，要求已知控制器的增益，很顯然這個條件約束性太強．

綜上分析，本文研究一類用T－S模型表示的模糊雙線性系統魯棒H∞控制問題．針對模糊雙線性模型，研究其魯棒穩定的條件，并且根據并行分布補償算法給出了魯棒控制器的設計，控制器可由一組線性矩陣不等式的解給出．本文和文［11] 相比，其不同之處在于：①控制器的增益可以通過線性矩陣不等式直接解出；②研究了系統的性能魯棒性．最后，由數例仿真驗證了結果的有效性．

注1：在本文中，Rn表示n維Euclidean空間，P＞0（P≥0）表示是一個正定（正半定）實對稱矩陣．在矩陣表達式中，用“＊”來表示對稱項，用diag｛…｝來表示對角陣．如果不做特別說明，矩陣均表示合適維數的矩陣．‖‖2表示歐氏范數．用來表示用來“I”來表示單位陣．如果不做特別說明，矩陣均表示合適維數的矩陣．

以下給出在證明中要用到的引理：

引理1［12]設M，N和F（t）是維數適合的實矩陣且滿足FT（t）F（t）≤I，則對于標量ε＞0，有如下不等式成立：

MTF（t）N＋NTFT（t）M≤εMTM＋ε－1NTN．

引理2［13]設A，D，E，F是合適維數的實數矩陣，且FT（t）F（t）≤I，則有矩陣P＞0，對于標量ε＞0滿足εI－HTH＞0時，有如下不等式成立：

（A＋DFE）TP（A＋DFE）≤ATPA＋ATPD（εIDTPD）－1DTPA＋εETE

1 系統的模型描述

由T－S模型描述的不確定模糊雙線性系統，它的第i條規則可描述如下：

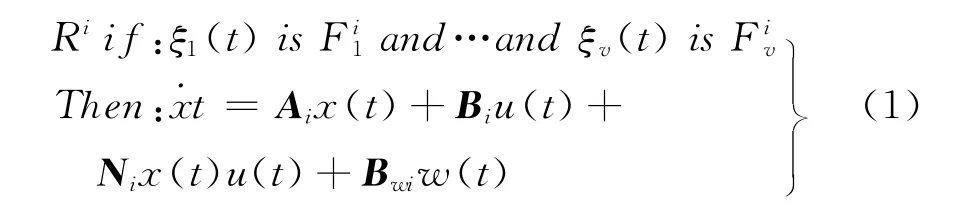
z（t）＝Cix（t） i∈I：＝｛1，2，…，s｝

假設：前提變量ξ（t）和控制變量及擾動變量無關；

通過單點模糊化，乘積推理和中心平均反模糊化方法，模糊控制系統的總體模型為

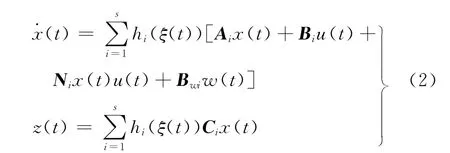
根據文［11] 的思想，根據并行分布補償算法，考慮模糊控制器：

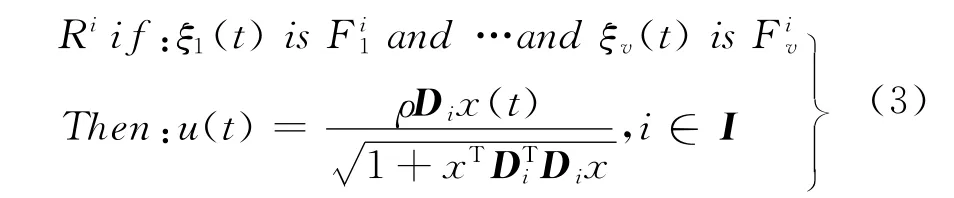
則整個系統的狀態反饋控制律可表示為

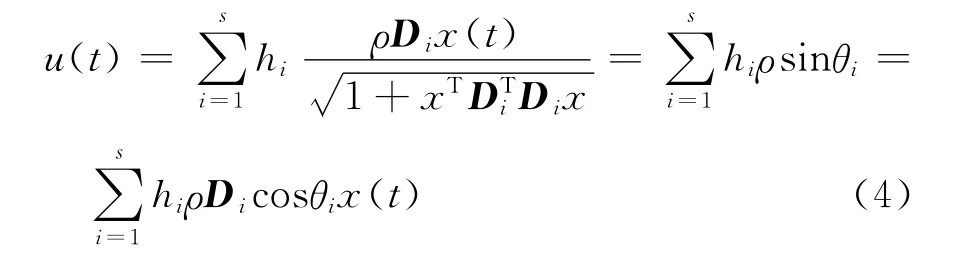
這里

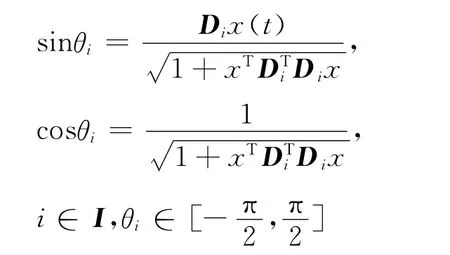
Di∈R1×n是待定的控制器增益，ρ＞0是待求的標量．

在控制律（4）的作用下，整個閉環系統的方程可表示為

定義1 對于給定的常數r＞0，以下條件滿足：

①ω（t）≡0時，閉環系統（5）是漸近穩定的；

②在零初始條件下，對任意非零ω（t）∈L2［0，∞），滿足‖z‖2＜r‖w‖2．

則稱系統（5）在H∞性能指標r下魯棒穩定．

本文目標：設計反饋控制律（4），使得系統（5）在H∞性能指標r下魯棒穩定．

2 魯棒穩定性分析和控制器設計

定理1 對于給定的r＞0，ρ＞0和常數ε1i，ε4i，εkij，k＝2，3；i，j∈I．如果存在著矩陣P＞0，Di，i∈I滿足下面矩陣不等式（6），則閉環系統（5）是H∞性能指標r下魯棒穩定的．

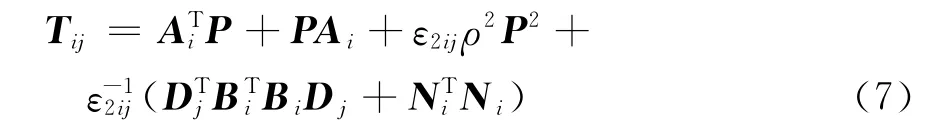
證明 選取如下Lyapunov函數：

其中：P＞0是待求的正定對稱矩陣．

首先，考慮w（t）≡0時系統（5）的漸近穩定性．

在w（t）≡0時，系統（5）可改寫為

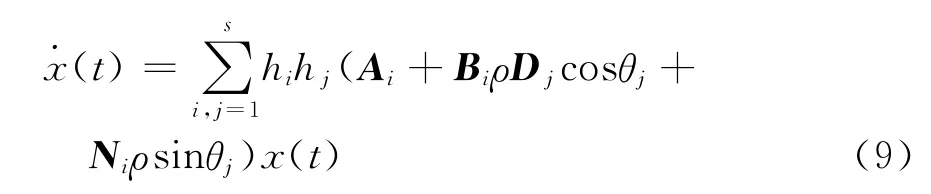
沿著系統（9）的軌線，對V（t）求導，可得到

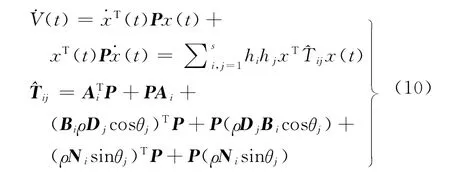
由引理1可知

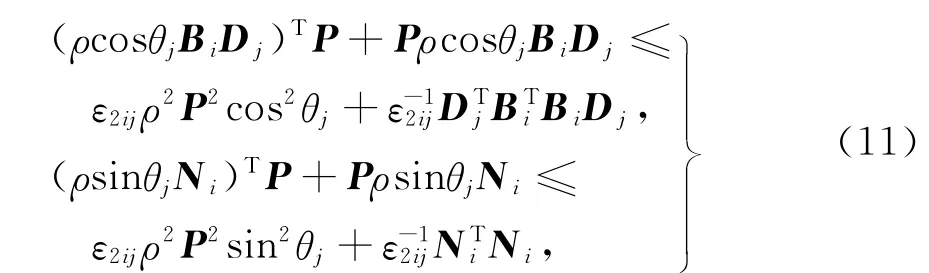
把式（11）帶入式（10），可得

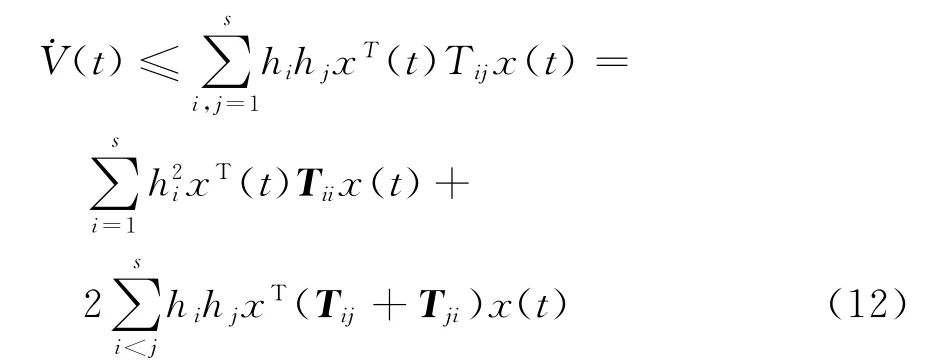
由定理1中式（6）可知：˙V（t）＜0，所以可知系統（5）是漸近穩定的．

以下考慮零初始條件ω（t）≠0時的系統（5）的魯棒H∞性能．沿著系統（5）的軌跡對V（t）求導，可得到

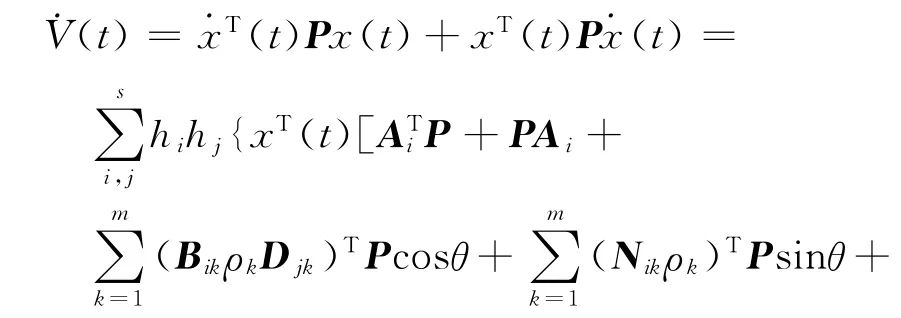
考慮

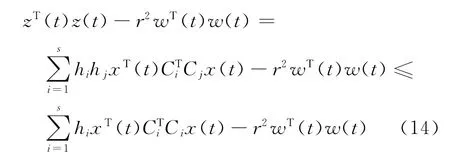
由引理2可知

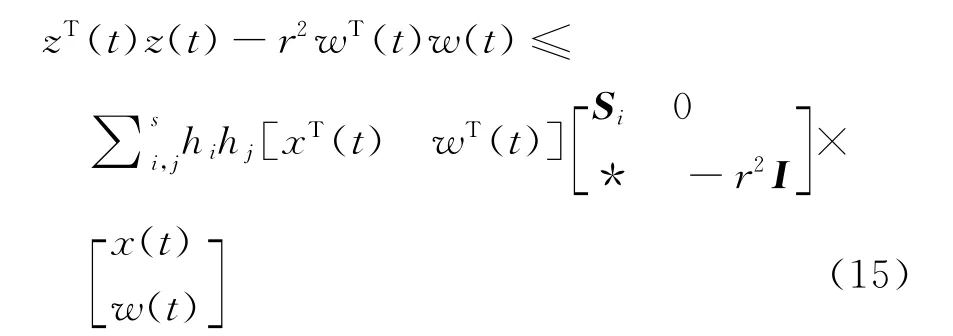
式（15）和式（13）相結合，可以得到

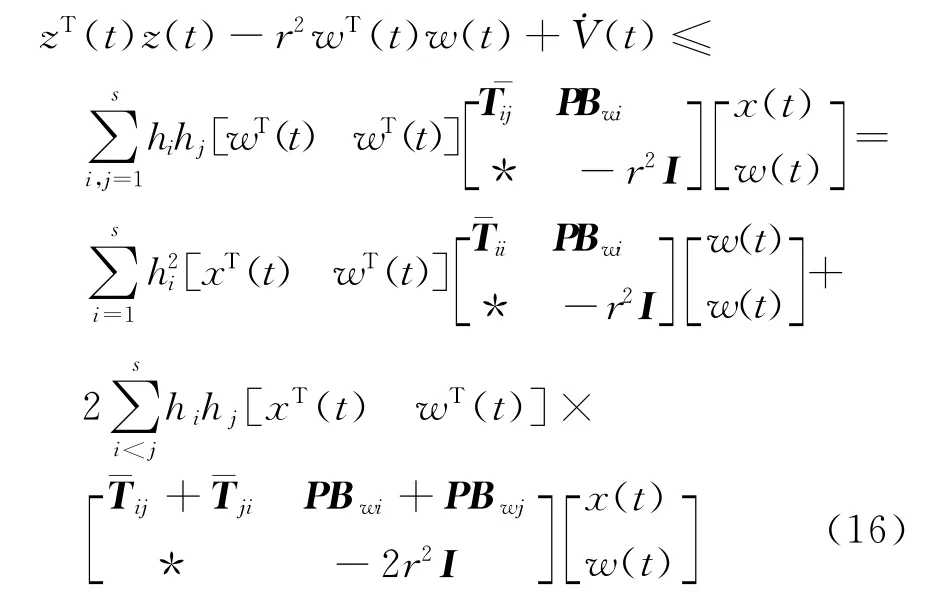
由定理1中式（6）可知

對式（17）積分可得到

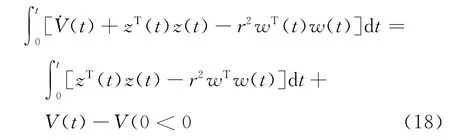
對式（18）取極限，令t→∞則可以得到：‖z‖2＜r‖w‖2．從而閉環系統（5）在H∞性能指標r下是魯棒穩定的．

3 算例分析

為了進一步闡述前面的方法和結論，考慮如下雙線性模糊系統：

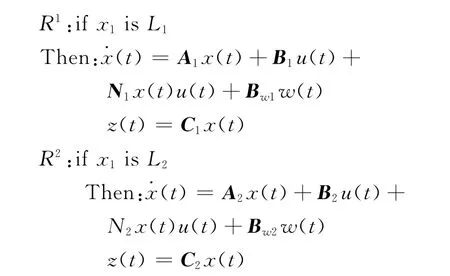
其中：

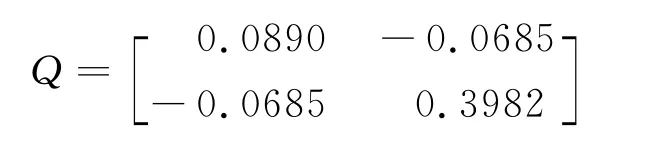
則正定陣及模糊增益矩陣分別為

分別選取初始值為［－0．8 －1．5] ，［－1．1 1．2] ，w（t）＝e－0．2t（sint），利用MATLAB仿真，圖1是系統變量x1和x2的狀態響應，圖2是控制律變化過程．由仿真結果可以看出，系統狀態變量在22s后趨于平衡點．

［1] Li T H S，Tsai S H．T–S fuzzy bilinear model and fuzzy controller design for a class of nonlinear systems［J] ．IEEE Trans．Fuzzy Syst．，2007，3（15）：494－506．

［2] Yang J，Jiao H N．Optimization and simulation of a fuzzy controller based on stochastic bilinear systems［J] ．2010International Conference on Electrical and Control Engineering，2010：1434－1438．

［3] Chiou J S，Kung F C，Li T S．Robust stabilization of a class of singularly perturbed discrete bilinear systems［J]．IEEE Trans．Autom．Control，2000，45（6）：1187－1190．

［4] Elliott D L．Bilinear systems in encyclopedia of electrical engineering［M]．New York：Wiley，1999．

圖1 系統分別在初始狀態：［－1 1．6] （實線）、［－2－1．6] （長劃線）下的狀態響應曲線

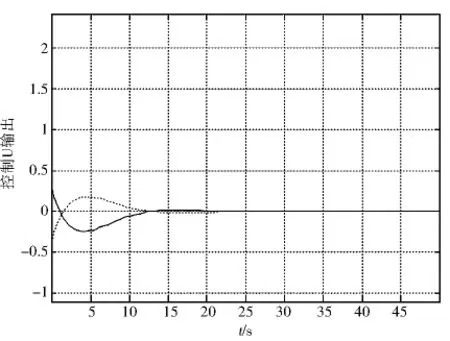
圖2 系統分別在初始狀態：［－1 1．6] （實線）、［－2－1．6] （長劃線）下的控制曲線

［5] Zhou S S，Lam J．Control design for fuzzy systems based on relaxed nonquadratic stability and H－infinity performance conditions［J] ．IEEE Trans．Fuzzy Syst．，2007，15（2）：188－198．

［6] Tanaka K，Sugeno M．Stability analysis and design of fuzzy control system［J] ．Fuzzy Sets and Systems，1992，45（2）：135－156．

［7] Kim E，Lee H．New approach to relaxed quadratic stability condition of fuzzy control systems［J] ．IEEE Ttans．Fuzzy Syst，2000，8（5）：523－533．

［8] Wu H N，Li H X．New approach to deladependent stability analysis and stabilization for continuous－times fuzzy systems with time－1varying delay［J] ．IEEE Trans．Fuzzy Systems，2007，15（3）：482－493．

［9] Chen B，Liu X P．Fuzzy guaranteed cost control for nonlinear systems with time－varying delay［J] ．IEEE Trans．Fuzzy Syst，2005，13（2）：238－249．

［10] Tanaka T，Ikeda T，Wang H O．Robust stabilizationof a class of uncertain nonlinear systems via fuzzy control：quadratic stability H－infinity control theory，and linear matrix inequalities［J] ．IEEE Trans．Fuzzy Syst．，1996，4（1）：1－13．

［11] Li T H S，Tsai S H．T－S fuzzy bilinear model and fuzzy controller design for a class of nonlinear systems［J] ．IEEE Trans．Fuzzy Systems．2007，3（15）：494－505．

［12] Tsai S H，Li T H S．Robust fuzzy control of a class fuzzy bilinear systems with time－delay［J] ．Chaos，Solitons and Fractals，2009，1（19）：796－801．

［13] Wang C W，Wang W Y，Chan M L．Design of sliding mode controllers for bilinear systems with time varying uncertainties［J] ．IEEE Trans．Syst．，Man Cybern，2004，3（4）：639－645．