基于小波的加外生變量部分線性自回歸模型在石油價格預測中的應用

井霞霞，張德生，李金鳳，王彥彪

（西安理工大學理學院，陜西西安710054）

準確的預測石油價格變動的方向和程度對國家制定能源政策和規避價格風險具有重要意義，對維護石油生產國和消費國的利益亦有重大意義．

目前預測石油價格的主要方法有時間序列法［1]、層次分析法［2]、灰色預測法［3]、回歸分析法［4]．時間序列模型主要有AR模型、ARMA［5]模型、ARIMA模型、VAR模型［8]、ARCH模型［9]、GARCH模型［10]、變系數回歸模型［11]等．

1 部分線性自回歸模型

部分線性模型［12]的一般形式為

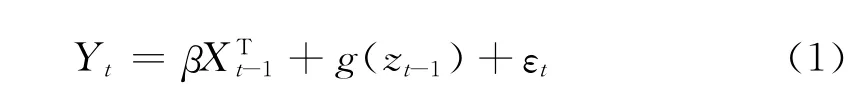
其中Xt－1＝（xt－1，1，…，∈Rp和Zt－1＝（zt－1，1，…∈Rq為解釋變量；β＝（β1，…，為未知參數向量，p和q是正整數，Yt∈R為響應變量或者是解釋變量．g（·）是未知函數，｛εt｝為隨機誤差序列，且εt＝Yt－E［Yt｜Xt－1，Zt－1] ，為線性時間序列部分，g（Zt－1）是非線性時間序列部分．在（1）式中，如果Xt－1和Zt－1中有一個是Yt的滯后變量，則（1）式就是部分線性自回歸模型．

2 小波多分辨分析

Meyer于1986年創造性地構造了具有一定衰減性的光滑函數，其二進制伸縮與平移構成L2（R）的規范正交基，才使小波得到真正的發展；1988年Mallat在構造正交小波基時提出了多分辨率的概念，從空間的概念上形象地說明了小波的多分辨率特性，將之前的所有正交小波基的構造法統一起來，給出了正交小波的構造方法以及正交小波變換的快速算法，即Mallat算法．Mallat算法在小波分析中的地位相當于快速傅立葉變換算法在經典傅立葉分析中的地位［13]．

定義1 設L2（R）的閉子空間序列｛vk，k∈Z｝稱為形成一個多分辨分析，若這些閉子空間｛Vk｝滿足以下性質：

1）單調性：Vm?Vm＋1，m∈Z．

3）伸縮性：

4）平移不變性：

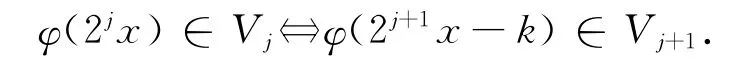
5）Riesz基存在性：存在Ψ（x）∈V0，使得｛φ（x－n）｜n∈Z｝構成子空間V0的Riesz基．

則稱｛Vk｝這些閉子空間成了L2（R）的一個多分辨分析，其中φ（x）稱為尺度函數，此時稱φ（x）生成了一個多分辨分析為｛Vk｝．

多分辨分析理論認為一個信號可以分解為低頻信號（概貌序列分量）和高頻信號（細節序列分量）兩部分．

3 基于小波的考慮外生變量的部分線性自回歸模型

3．1 建模步驟

對WTI石油價格進行建模預測時，具體步驟如下：

（1）利用小波變換對WTI現貨價格序列和世界供應量分別進行分解和重構，得到相應的概貌序列分量和細節序列分量，然后對他們分別進行平穩性檢驗和平穩化處理．

（2）利用概貌石油價格序列分量和概貌世界供應量序列分量建立部分線性自回歸模型．

（3）對細節石油價格序列分量和細節世界供應量序列分量也建立部分線性自回歸模型．

（4）將WTI現貨概貌價格和細節價格的預測結果進行求和，可以得到最后的WTI現貨預測價格

3．2 樣本選取

本文所選取的數據是2004年1月到2011年2月的WTI現貨價格和世界供應量的月度數據共86個，數據來源于美國能源情報署（http：／／www．eia．doe．gov／），前80個數據用于建模，后6個數據用來評價模型的質量．

3．3 小波分解與重構

對WTI現貨價格序列采用Sym2小波進行一層小波分解與重構，得到低頻的概貌序列CA1和高頻的細節序列CD1，如圖1所示．從圖1可以看出，在一層分解重構下得到的概貌序列基本上已經反映了WTI現貨價格序列的波動趨勢，而細節序列則體現了WTI現貨價格序列的隨機波動，分解的效果較好．同樣對世界供應量用Sym2小波進行小波分解和重構，得到相應的概貌序列和細節序列．

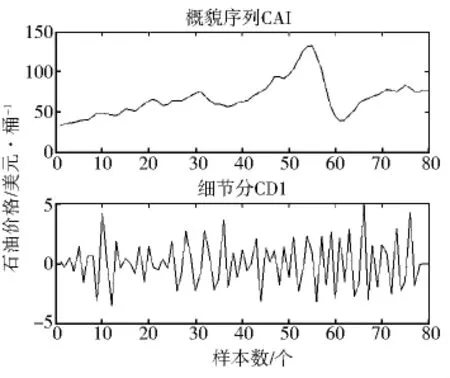
圖1 分解與重構后的概貌序列和細節序列

3．4 平穩性檢驗和預處理

在建立模型之前需要對WTI現貨價格和世界供應量進行小波分解和重構后的概貌序列和細節序列進行平穩性檢驗和平穩性處理，采用ADF檢驗法對概貌序列和細節序列分別進行檢驗，見表1．WTI現貨價格和世界供應量的概貌序列的ADF檢驗結果的統計量都大于各顯著性水平的臨界值，所以應該接受原假設，即WTI現貨價格和世界供應量的概貌序列并不平穩，經過對數差分后，ADF檢驗結果的統計量均小于各顯著性水平的臨界值，所以應該拒絕原假設，即序列平穩，而它們的高頻序列由表1可以看出已經平穩，故不需要處理．

3．5 部分線性自回歸模型的建立

對經過平穩化處理后的WTI現貨價格小波分解重構后的概貌序列進行建模，其中參數部分選取WTI現貨價格，非參數部分選擇世界供應量．建立的部分線性自回歸模型的表達式為

表1 ADF檢驗結果

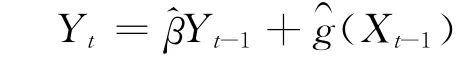
對WTI現貨價格經過小波分解的細節序列進行建模，建立的部分線性自回歸模型的表達式為

通過以上兩個模型可以分別得到建模數據的概貌序列和細節序列的擬合值，應用MATLAB編程，將WTI現貨價格概貌序列的擬合值進行還原，并與細節序列的擬合值進行相加得到WTI現貨價格最終的擬合值．

基于小波的考慮外生變量的部分線性自回歸模型對WTI現貨價格的擬合值和真實值比較結果如圖2所示．從圖2可以看出，基于小波的考慮外生變量的部分線性自回歸模型對WTI現貨價格月度數據時間序列的擬合效果比較準確．

圖2 部分線性自回歸模型擬合圖

3．6 部分線性自回歸模型的檢驗

當建立好一個時間序列模型時，需要檢驗隨機誤差項｛εt｝是否是一個白噪聲，若是則可以認為所建模有效，本文利用χ2檢驗法來進行檢驗，其主要思想是將εt的自相關系數記為ρk（N，εt），自協方差函數記為γk（N，εt），則

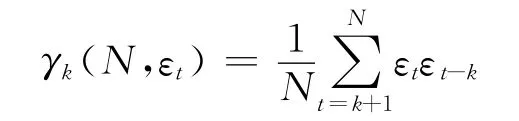
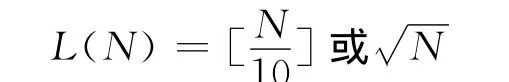
假設1 H0～NID（0，1），那么，即Q＝服從自由度為L（N）－M的χ2分布，L（N）為自相關系數的個數，M為模型的參數個數，于是，在給定顯著性水平α下，若Q≤（L（N）－M）接受H0；若Q＞（L（N）－M）則拒絕H0，即否定εt獨立．

由于εt是隨機的，這里我們用＝Yt－，t＝1，2，…，N來表示．所以由上述分析可知N＝80，L（N）＝10，M＝1，故L（N）－M＝9；當α＝0．05時，查χ2分布表可知（L（N）－M）＝（10－1）＝（9）＝16．919

概貌序列所建模型的統計量Q＝14．7023＜16．919，所以有95%的置信度認為殘差序列是白噪聲序列，因此，所建立的部分線性自回歸模型是有效的．

細節序列所建模型的統計量Q＝2．2243＜16．919，所以有95%的置信度認為殘差序列是白噪聲序列，因此，所建立的部分線性自回歸模型是有效的．

3．7 模型的預測比較

為了更好的研究所建立的模型的優劣，對部分線性自回歸模型、考慮外生變量的部分線性自回歸模型和基于小波的考慮外生變量的部分線性自回歸模型的預測結果進行比較，結果見表2，并計算出其平均絕對誤差和均方誤差，結果見表3．

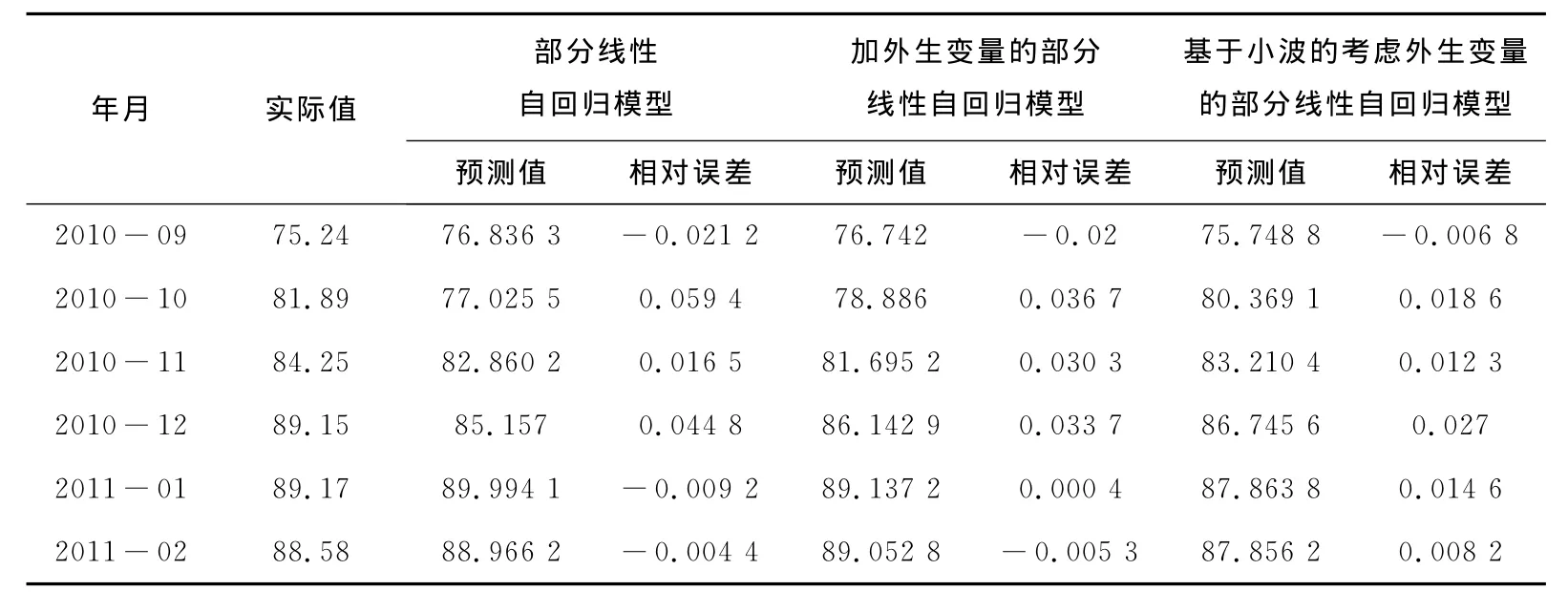
表2 3種模型的預測效果及其比較 美元／桶

表3 預測結果的MAE和MSE的比較

相對誤差＝（實際值—預測值）／實際值．

實證結果表明，對部分線性引入外生變量后，提高了模型的解釋能力，從表3中可以看出預測精度得到了一定的提高，將小波與考慮外生變量的部分線性自回歸模型結合以后，預測精度得到了進一步的提高．

4 結束語

本文對WTI現貨價格序列建立了基于小波的且考慮外生變量的部分線性自回歸預測模型，并將該模型與部分線性自回歸預測模型和考慮外生變量的部分線性自回歸預測模型進行了比較分析，因為該模型既利用了小波分析良好的局部化特性，又考慮了外生變量對外界影響因素的響應性，因此具有較高的預測精度．

［1] Granger C W J，and New bold．Spurious regession in econonetrics［J] ．Journal of Econometrics，1974，2：111－120．

［2] Yang C W，Hwang M J，Huang B N，An analysis of factors affecting price volatility of the US011market［J] ．Energy Economics，2002，24：107－119．

［3] 華澤澎，方紅松．國際油價的影響因素分析及中長期趨勢預測［C] ／／國際石油經濟研討會論文集，1995：43－51．

［4] Hsu L C，Applying the grey prediction model to the global integrated circuit industry［J] ．Technological Forecasting ＆Social Change，2003，70：563－574．

［5] 周明磊．事件對國際石油價格影響的時間序列分析［J] ．數學的實踐與認識，2004（8）：12－18．

［6] 丁靜之，林怡．ARIMA模型在石油價格預測中的應用［J] ．物流技術，2008，27（10）：156－160．

［7] 肖龍階，仲偉俊．基于ARIMA模型的我國石油價格預測分析［J] ．南京航空航天大學學報：社會科學版，2009，11（4）：41－46．

［8] 蔡純．石油價格波動金融影響因素的實證研究——基于月度數據的VAR模型分析［J] ．價格理論與實踐，2009（10）：52－53．

［9] 潘慧峰，張金水．基于ARCH類模型的國內油價波動分析［J] ．統計研究，2005（4）：16－20．

［10] 鄒艷芬，陸宇海．基于GARCH模型的石油價格變動模擬［J] ．數理統計與管理，2006，25（6）：640－644．

［11] 舒通．基于變系數回歸模型的石油價格預測［J] ．數理統計與管理，2008，27（5）：815－820．

［12] 柴根象，洪圣巖．半參數回歸模型［M] ．合肥：安徽教育出版社，1995．

［13] 程正興．小波分析算法與應用［M] ．西安：西安交通大學出版社，1998．