改進GM（1，1）模型在營養狀況預測中的應用

齊予侖

（喀什師范學院數學系，新疆喀什844000）

自20世紀80年代鄧聚龍先生針對“少數據、貧信息”問題提出灰色理論以來，灰色系統理論在很多領域得到了廣泛的應用，基于貧信息的灰預測成功地解決了許多信息不完全的預測問題．對于灰色預測GM（1，1）模型，很多文獻從模型的初值優化、灰導數、背景值等方面對其進行了改進，豐富了灰色系統理論的研究，并將GM（1，1）模型應用于經濟管理、工程與科學技術等許多領域．本文通過建立改進的灰色GM（1，1）模型，并利用根據中國學生體質與健康調研報告中4種營養性疾病檢出率（輕度營養不良、中度以上營養不良、超重、肥胖）的數據資料，對2010年和2015年我國10～12歲城鄉男女的營養性疾病檢出率進行預測．

1 改進GM（1，1）預測模型

設非負原始數據序列為x（0）＝｛x（0）（1），…，x（0）（n）｝，其累加生成序列x（1）＝｛x（1）（1），…，x（1）（n）｝．其中x（1）（k）＝，k＝1，2，…，n．稱x（0）（k）＋az（1）（k）＝b為GM（1，1）模型，這里z（1）（k）＝0．5x（1）（k）＋0．5x（1）（k－1）稱為GM（1，1）模型的背景值，為累加生成序列的緊鄰均值生成值．

若將背景值序列改為

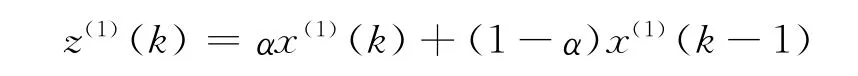
則可得

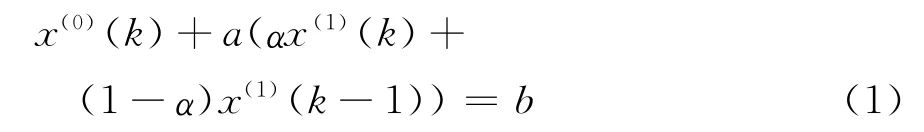
如果給定α的值，則可得（1）式中參數a，b的最小二乘估計為

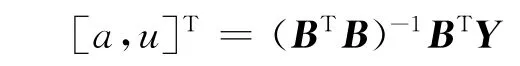
其中

進一步規定模型初值條件為t＝1時，x（1）（1）＝x（0）（1）＋β，這里β為初值修正參數．為了討論方便，將上面同時修正背景值和初值條件的灰色模型稱為改進GM（1，1）模型，從而改進GM（1，1）模型的時間響應函數為

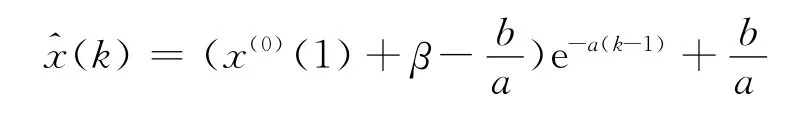
k＝1，2，…

還原后模型表達式為

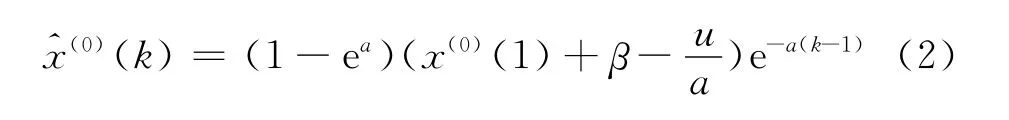
2 基于粒子群算法的改進GM（1，1）模型參數優化

粒子群優化算法［10]（Particle Swarm Optimization，PSO）是由James Kennedy和Russell Eberhart在1995年提出的，粒子群優化算法是一種智能進化計算技術，它具有計算簡單、收斂速度快，并且需要調整的參數少等優點，已經應用在方程優化、神經網絡訓練、系統控制以及模式識別等許多領域．

粒子群優化算法首先對目標函數初始化一組隨機解，每個個體解可以看成一個粒子．每個粒子都有一個由目標函數決定的適應值，還有一個速度決定粒子搜索的方向和距離．依據適應值的大小可以判斷粒子的優劣．在迭代過程中，每個粒子都根據兩個極值來更新自己，一個是個體極值（pbest），另一個是全局極值（gbest）．每個粒子都按照下面的公式更新自己的速度和位置

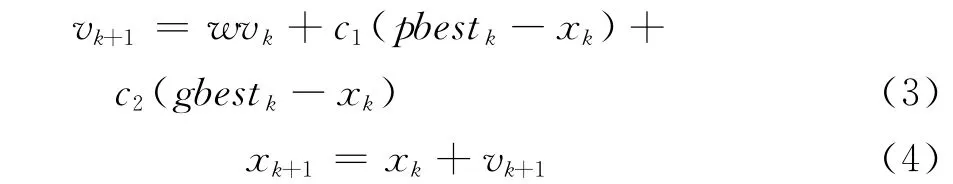
其中：vk是粒子的速度向量；xk是粒子的當前位置；pbestk是粒子本身搜索到的最優解，即個體極值；gbestk是整個粒子群搜索到的全局極值；w為慣性系數，用來保持全局搜索和局部搜索的平衡；c1和c2稱為加速系數，通常取（0，2）之間的隨機數．

根據一次累加生成序列的曲線形狀，可以大致判定參數a和b的取值范圍，作為約束條件，從而參數優化問題轉化為以平均相對誤差函數最小為目標的非線性優化問題，然后就能夠利用粒子群優化算法求解參數．

適應度函數是微粒群中各個微粒演化的評價函數，它需要根據具體問題來確定．這里將平均相對誤差函數作為適應度函數，利用粒子群算法確定改進GM（1，1）模型的參數優化．定義平均相對誤差函數為

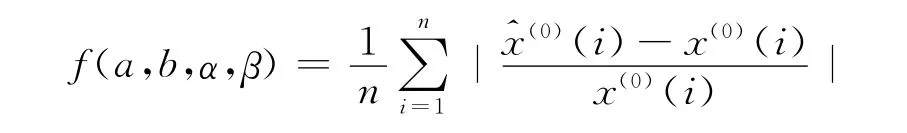
利用粒子群優化算法得到參數a，b，α，β的估計值，將這些估計值代入（1）式和（2）式就可以得到改進灰色GM（1，1）模型的時間響應函數．

粒子群優化算法辨識模型參數的算法步驟如下：

Step1 在可行域內初始化粒子種群和粒子速度；

Step2 計算每個粒子的適應值，選擇個體極值和全局極值；

Step3 如果計算結果達到一定的精度或者達到最大迭代次數，轉入Step5，否則轉入Step4；

Step4 按照（3）式和（4）式更新每個粒子的速度和位置，然后轉入Step2；

Step5 輸出全局極值以及相應的解，并退出循環．

3 學生營養健康狀況預測

學生的生長發育著重與營養有關，營養主要從日常膳食中攝取，生活水平和生活質量是改善與提高學生營養狀況的基礎條件，合理營養與科學營養是促進學生正常生長發育的基本保證．若營養攝取不均衡或營養過剩，都將嚴重影響學生正常發育與健康成長，其中營養不良和肥胖是新時期威脅我國學生健康常見的營養問題．因此，對學生的營養不良、超重和肥胖等營養性亞健康疾病的流行趨勢進行科學預測，可為國家今后一個時期有效實施對全國學生生長發育的宏觀監控，研究制定學校體育衛生工作發展規劃和促進學生生長發育的干預策略、措施提供科學數據．

數據資料來自1985、1995、2000、2005年中國學生體質與健康調研報告［11]，各時期全國學生各種營養狀況的篩查標準，統一使用“1985年身高標準體重”修訂版．該篩查方法同2003年公布“中國學齡兒童青少年超重、肥胖篩查BMI參考標準”的評價效果基本相一致，能比較客觀地反映不同時期我國學生的各種營養狀況．身高標準體重篩查法將學生營養狀況共分為7類：重度營養不良、中度營養不良、輕度營養不良、較低體重、正常體重、超重和肥胖．本文僅采用10～12歲城鄉男女的超重和肥胖指標數據資料（見表1）建立改進GM（1，1）模型，其它各年齡段可以采用類似方法．

這里以全國10～12歲鄉村女生營養性疾病檢出率中超重指標數據為例，說明建模的方法和過程．此時，原始數據序列和一次累加生成序列分別為

x（0）＝｛2．83，3．985，5．14，6．83，8．84｝

x（1）＝｛2．83，6．815，11．955，18．785，27．625｝

利用粒子群優化算法的基本參數設置為：加速系數c1＝c2＝2，迭代次數為20，慣性權重w＝0．2，模型參數α和β的取值范圍為α∈［0，1] ，β∈［0，5] ．利用Matlab軟件編程計算可得：α＝0．527 3，a＝－0．265 8，u＝2．691 4，β＝0．146 5．進一步可得改進GM（1，1）模型的擬合值，計算結果見表2．

表1 全國10～12歲學生1985 2005年2種營養性疾病檢出率 %

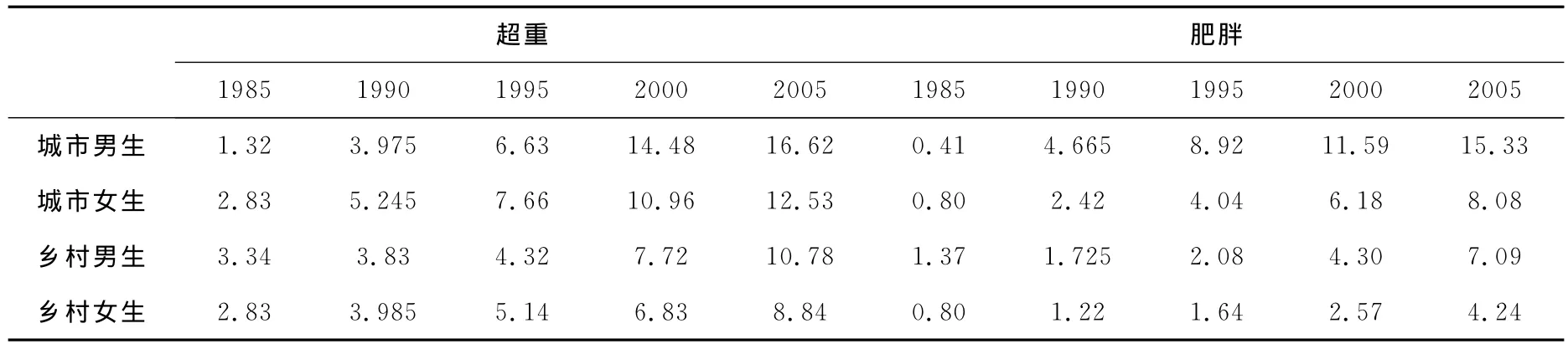
表1 全國10～12歲學生1985 2005年2種營養性疾病檢出率 %

注：表1中1990年數據是利用內插法得到的，其余數據選自中國學生體質與健康調研報告［11]

_________________________超重肥胖________________________________________1985 1990 1995 2000 2005 1985 1990 1995 2000 2005__城市男生1．32 3．975 6．63 14．48 16．62 0．41 4．665 8．92 11．59 15．33城市女生2．83 5．245 7．66 10．96 12．53 0．80 2．42 4．04 6．18 8．08鄉村男生3．34 3．83 4．32 7．72 10．78 1．37 1．725 2．08 4．30 7．09__鄉村女生____2．83 3．985 5．14 6．83 8．84 0．80 1．22 1．64 2．57 4．24__

表2 模型擬合值與實際值的比較分析

由表2的計算結果可以看出，改進GM（1，1）模型的平均相對誤差為0．383 654 537%，而GM（1，1）模型的平均相對誤差為0．508 877 303%．另外，改進GM（1，1）模型的均方差比也要小于傳統GM（1，1）模型的均方差比．結果表明，通過背景值和初值同時優化的改進灰色GM（1，1）模型能夠提高模型的擬合精度．

對表1的另外7組數據可以采用類似的方法建立改進GM（1，1）預測模型，計算結果都表明改進的GM（1，1）模型的擬合精度要比傳統的GM（1，1）模型的擬合精度高，這樣就可以利用這些改進GM（1，1）預測模型對未來學生營養性疾病檢出率進行預測，2010年和2015年城市男女生學生超重和肥胖指標，以及鄉村男女生學生超重和肥胖指標的預測結果見表3．

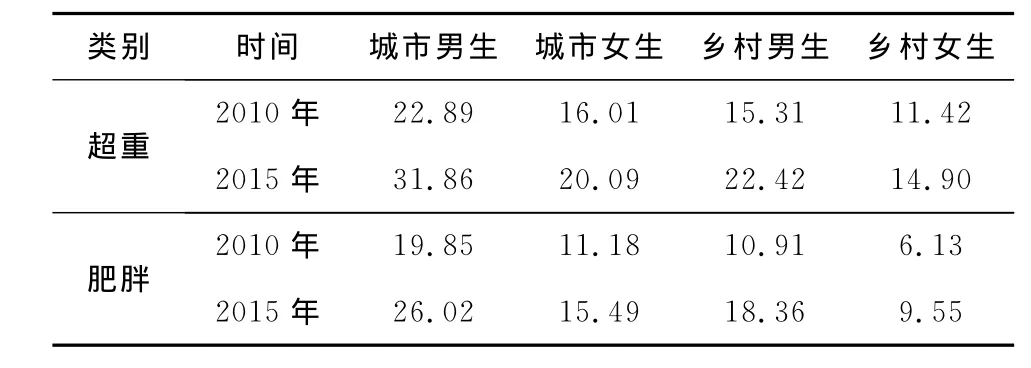
表3 全國10～12歲學生2種營養性疾病檢出率預測值 ﹪

表3的預測結果表明，未來時期我國學生中的超重與肥胖學生群體將在2005年的基數上大幅上升，且城市男生上升幅度最為明顯，成為未來時期重點干預的肥胖學生群體．此外，未來時期農村肥胖學生（男生）上升速度加快，成為未來時期最需要關注的易感肥胖流行群體，要警惕農村地區肥胖學生快速增長的苗頭與跡象．因此，今后一個時期要特別關注我國學生營養的雙面效應，應盡早采取積極主動的干預策略與措施，以期控制并減緩超重與肥胖學生群體的增長數量與增長速度．

4 結束語

提高灰色GM（1，1）預測模型擬合精度的途徑有很多種，同時優化模型的背景值和初值是提高灰色模型擬合精度的有效途徑之一．本文就是通過同時對GM（1，1）預測模型的背景值和初值條件進行修正，建立了改進GM（1，1）預測模型，并利用粒子群優化算法對改進模型的參數進行了優化．最后利用改進GM（1，1）預測模型對我國10～12歲城鄉男女生營養性疾病檢出率進行了預測．應用實例的計算結果表明：粒子群優化算法是優化改進GM（1，1）預測模型參數的一種有效方法，該算法具有計算簡便的特點．

［1] 王豐效．基于初值修正的非等間距灰色預測模型［J] ．重慶師范大學學報，2006，23（3）：42－44．

［2] 李玻，魏勇．優化灰導數后的新GM（1，1）模型［J] ．系統工程理論與實踐，2009（2）：100－105．

［3] 王豐效，張凌霜．基于蟻群算法的灰色組合預測模型［J] ．數學的實踐與認識，2009，39（14）：102－106．

［4] 王鐘羨，吳春篤，史雪榮．非等間距序列的灰色模型［J] ．數學的實踐與認識，2003，33（10）：16－20．

［5] 王豐效．非等間距組合灰色預測模型［J] ．數學的實踐與認識，2007，37（21）：39－43．

［6] 王豐效．非等距灰色預測模型的應用［J] ．統計與決策，2006（10）：20－21．

［7] 王豐效．GM（1，1）組合預測模型及其應用［J] ．統計與決策，2006（11）：142－143

［8] 宋中民．灰色GM（1，1）模型參數的優化方法［J] ．煙臺大學學報：自然科學與工程版，2001，14（3）：161－163．

［9] 張輝，胡適耕．GM（1，1）模型的邊值分析［J] ．華中科技大學學報，2001，29（4）：110－111．

［10] Kennedy J，Eberhart R．A new optimizer using particle swarm theory［C] ／／Proceedings of the Sixth International Symposium on Micromachine and Human Science．Piscataway，NJ：IEEE Service Center，1995：39－43．

［11] 中國學生體質與健康調研組．2005年中國學生體質與健康調研報告［M] ．北京：高等教育出版社，2007．